day-19 多种优化模型下的简单神经网络tensorflow示例

        如下样例基于tensorflow实现了一个简单的3层深度学习入门框架程序，程序主要有如下特性：

        1、  基于著名的MNIST手写数字集样例数据：http://yann.lecun.com/exdb/mnist/

        2、  加入衰减学习率优化，使得学习率可以根据训练步数指数级减少，在训练后期增加模型稳定性

        3、  加入L2正则化，减少各个权重值大小，避免过拟合问题

        4、  加入滑动平均模型，提高模型在验证数据上的准确性

        网络一共3层，第一层输入层784个节点的输入层，第二层隐藏层有500个节点，第三层输出层有10个节点。

# 导入模块库
import tensorflow as tf
import datetime
import numpy as np

# 已经被废弃掉了
#from tensorflow.examples.tutorials.mnist import input_data
from tensorflow.contrib.learn.python.learn.datasets import mnist
from tensorflow.contrib.layers import l2_regularizer

# 屏蔽AVX2特性告警信息
import os
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'

# 屏蔽mnist.read_data_sets被弃用告警
import logging
class WarningFilter(logging.Filter):
    def filter(self, record):
        msg = record.getMessage()
        tf_warning = 'datasets' in msg
        return not tf_warning
logger = logging.getLogger('tensorflow')
logger.addFilter(WarningFilter())


# 神经网络结构定义：输入784个特征值，包含一个500个节点的隐藏层，10个节点的输出层
INPUT_NODE = 784
OUTPUT_NODE = 10
LAYER1_NODE = 500

# 随机梯度下降法数据集大小为100，训练步骤为30000
BATCH_SIZE = 100
TRAINING_STEPS = 30000

# 衰减学习率
LEARNING_RATE_BASE = 0.8
LEARNING_RATE_DECAY = 0.99

# L2正则化
REGULARIZATION_RATE = 0.0001
MOVING_AVERAGE_DECAY = 0.99

validation_accuracy_rate_list = []
test_accuracy_rate_list = []


# 定义前向更新过程
def inference(input_tensor,avg_class,weights1,biase1,weights2,biase2):
    if avg_class == None:
        layer1 = tf.nn.relu(tf.matmul(input_tensor,weights1) + biase1)
        return tf.matmul(layer1,weights2) + biase2
    else:
        layer1 = tf.nn.relu(tf.matmul(input_tensor,avg_class.average(weights1)) + avg_class.average(biase1))
        return tf.matmul(layer1,avg_class.average(weights2)) + avg_class.average(biase2)

# 定义训练过程
def train(mnist_datasets):
    # 定义输入
    x = tf.placeholder(dtype=tf.float32,shape=[None,784])
    y_ = tf.placeholder(dtype=tf.float32,shape=[None,10])

    # 定义训练参数
    weights1 = tf.Variable(tf.truncated_normal(shape=[INPUT_NODE,LAYER1_NODE],mean=0.0,stddev=0.1))
    biase1 = tf.Variable(tf.constant(value=0.1,dtype=tf.float32,shape=[LAYER1_NODE]))
    weights2 = tf.Variable(tf.truncated_normal(shape=[LAYER1_NODE,OUTPUT_NODE],mean=0.0,stddev=0.1))
    biase2 = tf.Variable(tf.constant(value=0.1,dtype=tf.float32,shape=[OUTPUT_NODE]))

    # 前向更新
    # 训练数据时，不需要使用滑动平均模型，所以avg_class输入为空
    y = inference(x,None,weights1,biase1,weights2,biase2)

    # 该变量记录训练次数，训练模型时常常需要设置为不可训练的变量，即trainable=False
    global_step = tf.Variable(initial_value=0,trainable=False)

    # 生成滑动平均模型，用于验证
    variable_averages = tf.train.ExponentialMovingAverage(decay=MOVING_AVERAGE_DECAY,num_updates=global_step)
    # 在所有代表神经网络的可训练变量上，应用滑动模型,即所有的可训练变量都有一个影子变量
    variable_averages_ops = variable_averages.apply(tf.trainable_variables())

    # 定义数据验证时，前向更新结果
    average_y = inference(x,variable_averages,weights1,biase1,weights2,biase2)

    # 计算交叉熵
    cross_entropy = tf.nn.sparse_softmax_cross_entropy_with_logits(labels=tf.argmax(y_,1),logits=y)
    cross_entropy_mean = tf.reduce_mean(cross_entropy)

    # 计算L2正则化损失
    regularizer = l2_regularizer(REGULARIZATION_RATE)
    regularization = regularizer(weights1) + regularizer(weights2)

    # 计算总损失Loss
    loss = cross_entropy_mean + regularization

    # 定义指数衰减的学习率
    learning_rate = tf.train.exponential_decay(learning_rate=LEARNING_RATE_BASE,global_step=global_step,
                                               decay_steps=mnist_datasets.train.num_examples / BATCH_SIZE,
                                               decay_rate=LEARNING_RATE_DECAY)

    # 定义随机梯度下降算法来优化损失函数
    train_step = tf.train.GradientDescentOptimizer(learning_rate=learning_rate)\
        .minimize(loss = loss,global_step = global_step)

    # 每次前向更新完以后，既需要反向更新参数值，又需要对滑动平均模型中影子变量进行更新
    # 和train_op = tf.group(train_step,variable_averages_ops)是等价的
    with tf.control_dependencies([train_step,variable_averages_ops]):
        train_op = tf.no_op(name='train')

    # 定义验证运算，计算准确率
    correct_prediction = tf.equal(tf.argmax(average_y,1),tf.argmax(y_,1))
    accuracy = tf.reduce_mean(tf.cast(x=correct_prediction,dtype=tf.float32))

    with tf.Session() as sess:
        init = tf.global_variables_initializer()
        sess.run(init)

        validate_feed = {x:mnist_datasets.validation.images,
                         y_:mnist_datasets.validation.labels}
        test_feed = {x:mnist_datasets.test.images,
                     y_:mnist_datasets.test.labels}

        for i in range(TRAINING_STEPS):
            # 每1000轮，用测试和验证数据分别对模型进行评估
            if i % 1000 == 0:
                validate_accuracy_rate = sess.run(accuracy,validate_feed)
                print("%s: After %d training steps(s),validation accuracy"
                      "using average model is %g "%(datetime.datetime.now(),i,validate_accuracy_rate))

                test_accuracy_rate = sess.run(accuracy, test_feed)
                print("%s: After %d training steps(s),test accuracy"
                      "using average model is %g " % (datetime.datetime.now(),i, test_accuracy_rate))

                validation_accuracy_rate_list.append(validate_accuracy_rate)
                test_accuracy_rate_list.append(test_accuracy_rate)

            # 获得训练数据
            xs,ys = mnist_datasets.train.next_batch(BATCH_SIZE)
            sess.run(train_op,feed_dict={x:xs,y_:ys})


# 主程序入口
def main(argv=None):
    mnist_datasets = mnist.read_data_sets(train_dir='MNIST_data/',one_hot=True)
    train(mnist_datasets)
    print("validation accuracy rate list:",validation_accuracy_rate_list)
    print("test accuracy rate list:",test_accuracy_rate_list)

# 模块入口
if __name__ ==  '__main__':
    tf.app.run()

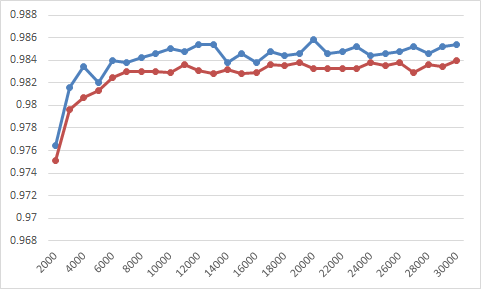
       每1000轮，使用测试和验证数据分别对模型进行评估，绘制出如下准确率曲线图，其中蓝色曲线表示验证数据准确率，深红色曲线表示测试数据准确率，不难发现，通过引入滑动平均模型，模型在验证数据上有更好的准确率。

       

       进一步，通过如下代码，我们对两个准确率求解相关系数：

import numpy as np
import math

x = np.array([0.1748, 0.9764, 0.9816, 0.9834, 0.982, 0.984, 0.9838, 0.9842, 0.9846, 0.985, 0.9848, 0.9854, 0.9854, 0.9838, 0.9846, 0.9838, 0.9848, 0.9844, 0.9846, 0.9858, 0.9846, 0.9848, 0.9852, 0.9844, 0.9846, 0.9848, 0.9852, 0.9846, 0.9852, 0.9854])
y = np.array([0.1839, 0.9751, 0.9796, 0.9807, 0.9813, 0.9825, 0.983, 0.983, 0.983, 0.9829, 0.9836, 0.9831, 0.9828, 0.9832, 0.9828, 0.9829, 0.9836, 0.9835, 0.9838, 0.9833, 0.9833, 0.9833, 0.9833, 0.9838, 0.9835, 0.9838, 0.9829, 0.9836, 0.9834, 0.984])

# 计算相关度
def computeCorrelation(x,y):
    xBar = np.mean(x)
    yBar = np.mean(y)
    SSR = 0.0
    varX = 0.0
    varY = 0.0
    for i in range(0,len(x)):
        diffXXbar = x[i] - xBar
        difYYbar = y[i] - yBar
        SSR += (diffXXbar * difYYbar)
        varX += diffXXbar**2
        varY += difYYbar**2
    SST = math.sqrt(varX * varY)
    return SSR/SST

# 计算R平方
def polyfit(x,y,degree):
    results = {}
    coeffs = np.polyfit(x,y,degree)
    results['polynomial'] = coeffs.tolist()
    p = np.poly1d(coeffs)
    yhat = p(x)
    ybar = np.sum(y)/len(y)
    ssreg = np.sum((yhat - ybar)**2)
    sstot = np.sum((y - ybar)**2)
    results['determination'] = ssreg/sstot
    return results

result = computeCorrelation(x,y)
r = result
r_2 = result**2
print("r:",r)
print("r^2:",r*r)
print(polyfit(x,y,1)['determination'])

        结果显示，二者相关系数大于0.9999，这意味着在MNIST问题上，完全可以模型在验证数据上的表现来判断模型的优劣。当然，这个仅仅是MNIST数据集上，在其它问题上，还需要具体分析。

C:\Users\Administrator\Anaconda3\python.exe D:/tensorflow-study/sample.py
r: 0.9999913306679183
r^2: 0.999982661410994
0.9999826614109977