day-14 回归中的相关系数和决定系数概念及Python实现

　　衡量一个回归模型常用的两个参数：皮尔逊相关系数和R平方

一、皮尔逊相关系数

　　在统计学中，皮尔逊相关系数( Pearson correlation coefficient），又称皮尔逊积矩相关系数（Pearson product-moment correlation coefficient，简称 PPMCC或PCCs），是用于度量两个变量X和Y之间的相关（线性相关），其值介于-1与1之间。

 　　

　　实际可用如下公式进行计算：

　　

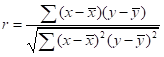
　　若大于0，表示正向相关，小于0，表示负向相关，等于0，表示不相关

二、决定系数：R平方值

         定义：反应因变量的全部变异能通过回归关系被自变量解释的比例。

        

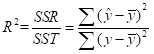
         特别的对于简单线性回归模型时：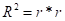

　　其中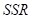（Sum square regression）表示所有预测值与平方值的变异量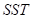，（Sum square total）表示所有真实值与平方值的变异量，（Sum square regression）表示真实值与预测值的变异量

        　　　　

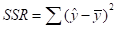
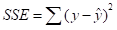
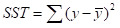
         例如当为0.8时，表示80%可以用模型来解释

         实际应用中，为了抵消样本数量对评估参数的影响，我们需要对R平方表示式进行修正为：

        

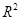         表示样本的R平方值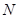，表示样本大小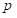，表示预测值数量

三、python代码实现

　　对于简单线性回归，分别计算相关系数和决定系数，并验证公式：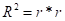

import numpy as np
import math

x = np.array([1,3,8,7,9])
y = np.array([10,12,24,21,34])

# 计算相关度
def computeCorrelation(x,y):
    xBar = np.mean(x)
    yBar = np.mean(y)
    SSR = 0.0
    varX = 0.0
    varY = 0.0
    for i in range(0,len(x)):
        diffXXbar = x[i] - xBar
        difYYbar = y[i] - yBar
        SSR += (diffXXbar * difYYbar)
        varX += diffXXbar**2
        varY += difYYbar**2
    SST = math.sqrt(varX * varY)
    return SSR/SST

# 计算R平方
def polyfit(x,y,degree):
    results = {}
    coeffs = np.polyfit(x,y,degree)
    results['polynomial'] = coeffs.tolist()
    p = np.poly1d(coeffs)
    yhat = p(x)
    ybar = np.sum(y)/len(y)
    ssreg = np.sum((yhat - ybar)**2)
    sstot = np.sum((y - ybar)**2)
    results['determination'] = ssreg/sstot
    return results

result = computeCorrelation(x,y)
r = result
r_2 = result**2
print("r:",r)
print("r^2:",r*r)
print(polyfit(x,y,1)['determination'])

　　通过结果验证，简单线性回归模型中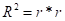，成立