day-10 sklearn库实现SVM支持向量算法

　　学*了SVM分类器的简单原理，并调用sklearn库，对40个线性可分点进行训练，并绘制出图形画界面。

一、问题引入

　　如下图所示，在x,y坐标轴上，我们绘制3个点A（1,1），B（2,0），C（2,3），其中A和B属于一类，C属于一类。

　　我们希望找到一条直线，将两个类分开来，且保持实线和两条虚线的距离最大，我们就能将两个类最大化分割开来。当然，我们还有很多其他直线的可以将两个点分割开来，但是这样分割效果最好。

　　当一个新的点进行预测时，根据点在直线的位置，判断所属分类。例如D（4,3）点在实线上方，判定为和C是一类。

　　源码：　　　　

# 导入基本库
from sklearn import svm
import pylab as pl
import numpy as np
# 初始化坐标点
x = np.zeros((3,2))
x[0] = [2,0]
x[1] = [1,1]
x[2] = [2,3]
y = [0,0,1]
# 建立一个SVM分类器，并进行预测
clf = svm.SVC(kernel='linear')
clf.fit(x,y)

# 打印出所有的支持向量点 
print(clf.support_vectors_)
# 根据方程w_0*x + w_1*y + w_3 = 0--> y = -w_0/w_1*x - w_3/w_1 = kx + b
# 根据w_0,w_1,w_3求得k和b
w = clf.coef_[0]
k = -w[0]/w[1]
b = -clf.intercept_[0]/w[1]
# 调用函数，初始化x点坐标范围
xx = np.linspace(start=0, stop = 5)
# 计算直线方程
yy = k*xx + b

# 获取第一个支持向量点，计算直线方程
b = clf.support_vectors_[0]
yy_down = k*xx + (b[1] - k*b[0])

# 获取最后一个支持向量点，计算直线方程
b = clf.support_vectors_[-1]
yy_up = k*xx + (b[1] - k*b[0])

# 绘制点和直线
pl.scatter(x[:,0],x[:,1])
pl.plot(xx,yy,'k-')
pl.plot(xx,yy_down,'k--')
pl.plot(xx,yy_up,'k--')
pl.scatter(x[:,0],x[:,1],c=y,cmap=pl.cm.Paired)
pl.scatter(4,3,c=y,cmap=pl.cm.Paired)
pl.show()

二、SVM分类简单介绍

　　最早是由 Vladimir N. Vapnik 和 Alexey Ya. Chervonenkis 在1963年提出，目前的版本(soft margin)是由Corinna Cortes 和 Vapnik在1993年提出，并在1995年发表，深度学*（2012）出现之前，SVM被认为机器学*中*十几年来最成功，表现最好的算法。

　　假设我们的测试数据为一个二维平面的点，如上图例子所示，我们定义一条直线方程为w_0*x + w_1*y + w_3 = 0，SVM算法的原理就是要根据训练集获取到参数w_0、w_1、w_3的值，即可利用该模型进行新的测试数据预测。对于参数的求导过程，可以参考下面链接：

　　https://www.zhihu.com/question/21094489

　　当我们无法找到一条直线，将不同类分割开来时，我们称之为线性不可分，否则为线性可分。例如下面所示为线性不可分的情况。对于线性不可分的情况，可以通过一定的映射关系，转换到其他平面，变成线性可分，例如二维左边转换为极坐标。

　　  

　　上面讨论的是只有两种分类，如果遇到大于2中分类的情况，我们可以用迭代分类点方式进行，例如有A,B,C三类，我们可以先将A,B化为一类，整体和C进行分类，如果属于A,B整体类，再对A,B进行分类，以此类推。

三、简单的SVM代码实现

　　程序效果图：对40个线性可分点进行训练，并绘制出图形界面。

 

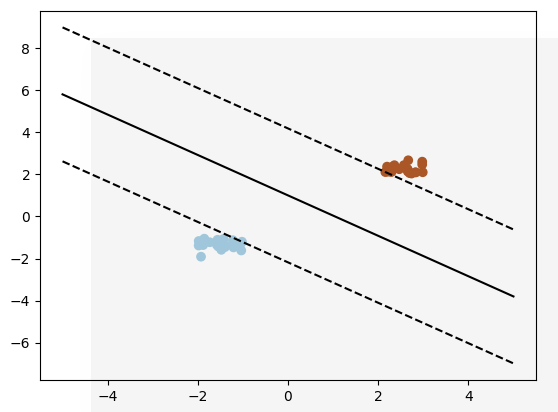
# 函数功能：以[2,2]为中心，随机产生上下40个线性可分的点，画出支持向量和所有的点

# 导入基本库
import numpy as np
import pylab as pl
from sklearn import svm

# 每次程序运行时，产生的随机点都相同
np.random.seed(0)

# 产生40行随机坐标，且线性可区分
x = np.r_[np.random.rand(20,2) - [2,2],np.random.rand(20,2) + [2,2]]
y = [0]*20 + [1]*20

# 创建一个SVM分类器并进行预测
clf = svm.SVC(kernel='linear')
clf.fit(x,y)

# 根据SVM分类器类参数，获取w_0,w_1，w3的值，并绘制出支持向量
# x_0*x + w_1 *y + w_3 = 0 --> y = -w0/w1*x - w_3/w_1 
w = clf.coef_[0]
a = -w[0]/w[1]
b = -clf.intercept_[0]/w[1]
xx = np.linspace(-5, 5)
yy = a*xx + b

# 斜距式方程：y = kx + b，A(b[0],b[1])为一个支持向量点
b = clf.support_vectors_[0]
yy_down = a*xx + (b[1] - a*b[0])

# 斜距式方程：y = kx + b，B(b[0],b[1])为一个支持向量点
b = clf.support_vectors_[-1]
yy_up = a*xx + (b[1] - a*b[0]) 

#画出3条直线
pl.plot(xx,yy,'k-')
pl.plot(xx,yy_down,'k--')
pl.plot(xx,yy_up,'k--')

#画出支持向量点
pl.scatter(clf.support_vectors_[:,0], clf.support_vectors_[:,1],
           s=80,facecolors = 'none')
pl.scatter(x[:,0],x[:,1],c=y,cmap=pl.cm.Paired)

# 绘制平面图
pl.axis('tight')
pl.show()

 四、学*总结

　　在学*过程中，重新复*了直线方程的表达式：两点式、点斜式、斜距式、截距式，以及点到直线的距离等。同时了解numpy库对于数组的基本操作。