机器人一阶运动学

回顾：https://www.cnblogs.com/pylblog/p/18529426

四关节机器人，可以末端关节位姿，表示为：

 假设，机器人末端关机位姿，简化为如下公式：

对齐求导，可得：

 对于附合导数，自然有：

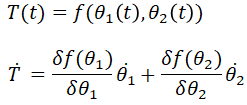
 T的导数，自然是姿态的变化速度（末端局部坐标系下，x = [1,0,0] 处的速度向量），和末端原点的运动速度向量

那最终，其形式，为：

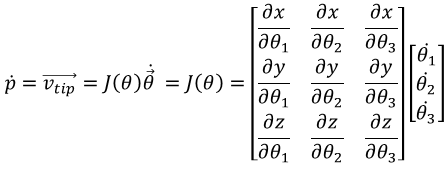
假设只对末端位置感兴趣（相当于取第4列），例如：

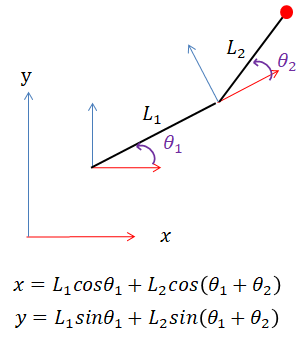
 那么，末端的速度向量：

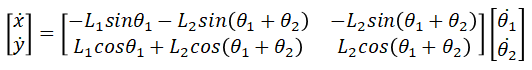
 那么，观测此公式，可以得到结论：

（1）给定θ₁，θ₂，得到了初始的位姿

（2）在下一刻进行运动，给得各个关节 运动、转动速度θ₁，θ₂ ，求得此刻端点的速度向量。

---

 

力矩

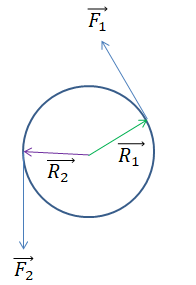
已知：

1. 圆中心固定，可以转动

2. F₁，F₂两个力大小相同，方向不同

作用方向相反的两个力，但作用于圆是一致的，所以用力矩表达：

 

速度与角速度关系

（以下公式都是标量，不考方向）

当 Δt 接近0时，弧长：

 数值上：

假设作用在切向方向的力为F，那么，对于功率P ：

因此：

 

---

以上公式的作用

假设末端关节，需要输出切向力 f_{tip ，}求各个关节应该输出的扭矩

那么，末端的功率为：

P = f_tip^Tv_tip （向量点积为标量）

同时，由于能量守恒，各个关节给出的功率：

为该关节力矩的大小，力矩的方向为旋转轴方向，所以：

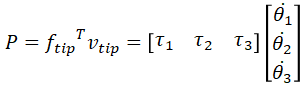
又：

因此：

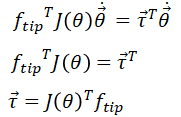
 如此得到各个关节要输出的力矩，就可以反馈给下位机了。

 

---

 矩阵基本知识

 当 AB = BA 时：

 那么，可以推导：

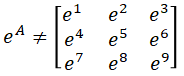
 所以记e^A =  f(A)

（对于旋转矩阵，若使用e^[ω]θ方式并展开，就可以得到罗德里格斯公式，所以有：R = e^[ω]θ = 罗德里格斯公式 ）

e^A  是 f(A) 的简写（只是恰巧有部分指数运算可以使用）

 若：

 那么：

因为：

---

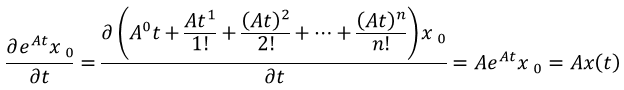
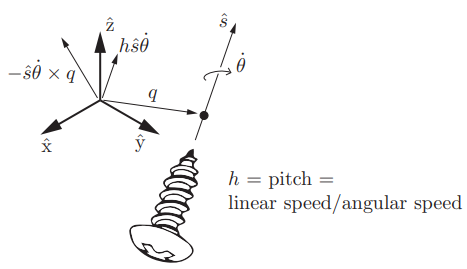
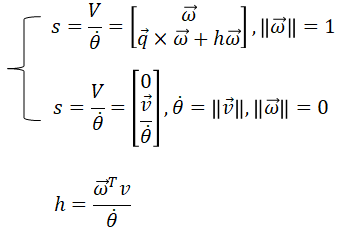
v = 切线速度 + 沿旋转轴方向的速度 ， 相当于关机总速度

（此方法推的V，是末端关节在s的总速度；而T^'T ^-1 推的V，则是整个s都移动下，s原点速度）

 疑问：使用几何方法V的方式，和使用T^'T ^-1 的v含义不同？

如果，不用几何的办法，纯粹推：

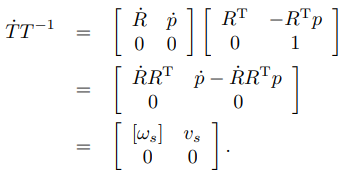
p' 是p点的线速度，v_s =  p'  - RR^Tp = p'  - [ω_s]p，不就相当于：总线速度 - 旋转引起的切向速度 =  沿旋转轴的速度

 

---

  空间雅可比矩阵

使用旋量方式计算末端关节位姿

 利用多元函数求导法则：

暂且不管两种求运动旋量的方式的冲突，认为已经得到了T，按照：

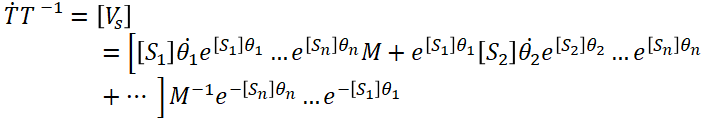
 令：

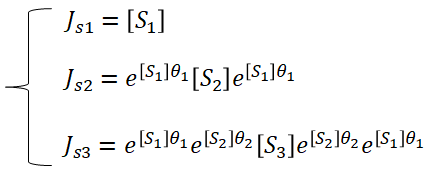
 那么，可以得到：

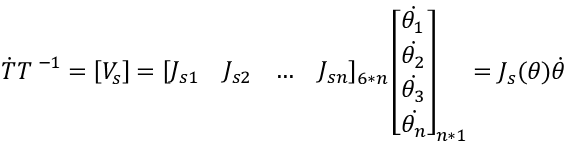
（先不管两种求运动旋量的方式的冲突，暂时认为一种是用来计算T，一种是用来计算[V_s]就行了）

J_s1、J_s2.....J_sn实际上，就是机械臂运动到θ₁、θ₂、θ₃时，各个关节的旋量

而推算T = e^[s1]θ1 e^[s2]θ2 e^[s3]θ3..M，则是使用θ₁ = 0、θ₂= 0、θ₃= 0，各个关节的旋量，参考：https://www.cnblogs.com/pylblog/p/18529426

例如：

  

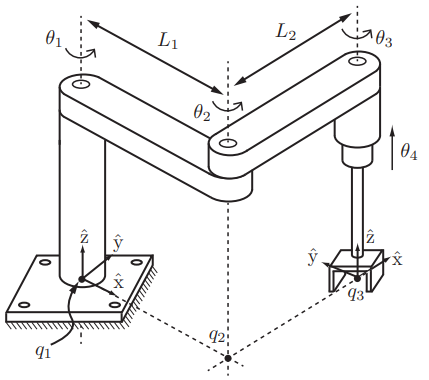
 J_s1：ω = [0,0,1]^T，v = -[ω] q =  -[ω] [0,0,0]^T

 J_s2：ω = [0,0,1]^T，v = -[ω] q =  -[ω] [ L₁s₁ , L₁c₁ , 0 ]^T = [ L₁s₁ ,  -L₁c₁ , 0 ]^T

 J_s3：ω = [0,0,1]^T，v = -[ω] q =  -[ω] [ L₁s₁ + L₂s₁₂ ,   L₁c₁ + L₂c₁₂, 0]^T = [ L₁s₁ + L₂s₁₂,   - L₁c₁ - L₂c₁₂, 0 ]^T

 J_s4：ω = [0,0,0]^T，v = [0,0,1] ，（对于移动关节的运动旋量，其ω为0，v为运动方向单位向量，θ 为速度）