运动控制理论（4）——逆解

p_w：世界坐标

P：最后一节点在最后一个坐标系下的局部坐标

在逆解中，Pw已知，P也已知，可以得到T，要由T得到θ_i，d_i （旋转和伸长）

正算的例子：

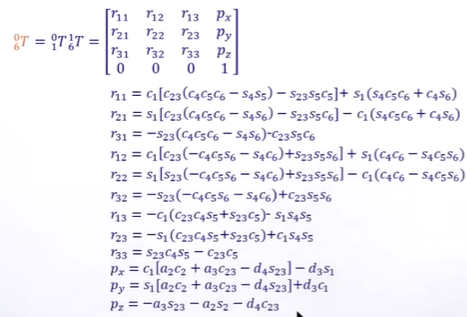
 一般来说，正算的时候，不会用矩阵相乘的办法，而是将每个元素单独算，节省CPU开销

 

3 个长度为1 + 3个相互垂直 = 6个限制条件

3*3矩阵 + 3*1向量 = 12条方程

6个未知数

独立（线性无关）方程数 > 未知数，那么就是有多解了。

 

---

 多解

 

---

 

求解方法：

一、解析法，分为：

（一）代数法 algebraic。直接在方程式上，做加减乘除，合并消去。（不就相当于手算了）

（二）几何法 geometric。用最后的几何，拆解成三角函数表示的方法。（是不是先算出手臂的各个向量，再反算角度？？？）

二、数值法。用电脑解方程。

* 目前大多数手臂设计成具有解析解。

* 解析解是real time控制中最快的。

 

 

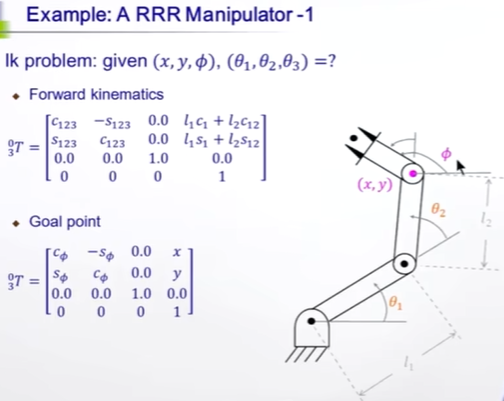
已知Φ，x，y

x,y，是世界坐标系下坐标，如果i = 3是末端，那么第4列就是x、y了

因为：https://www.cnblogs.com/pylblog/p/17962142

Pw  = T⁰₃ P

P = [a3 , 0, 1]，将P写出一个平移矩阵，就是上面例子的 ⁰₃T

所以：⁰₃T 阵的每个元素，都可以根据给定Φ，x，y得到具体值，然后再推算θ₁，θ₂，θ₃

（这点尤其重要，必须知道⁰₃T 阵的每个元素的具体值）

 

---

 

 

---

 

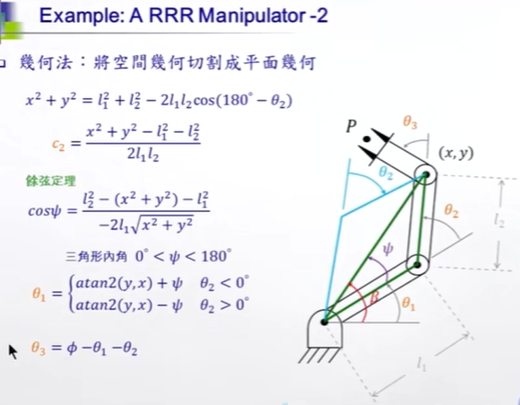
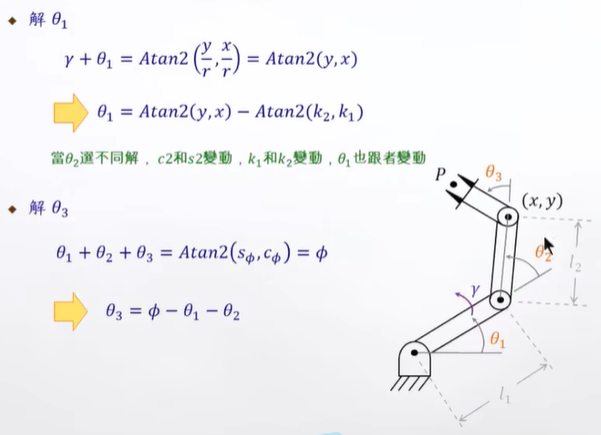
复杂的三角函数求解：

 

---

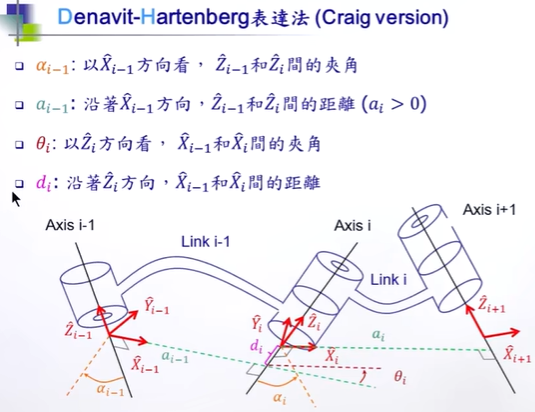
先知道"手腕"的位置，获得θ1，θ2，θ3。

用Craig定义方式，得到通用的转换阵

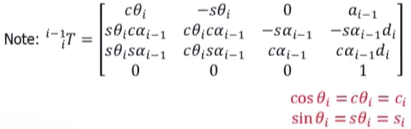
按照定义的步骤，一步步变过去，第四列就是变换后原点的坐标。

P_i = T ⁱ_i-1* P_i-1， 当 P_i-1 = [ 0,0,0,1 ]^T，即局部坐标系下的原点，那么T ⁱ_i-1 的第四列，则为P_i

令：

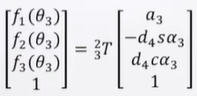
因为对于上面那个手臂：

沿X₃方向看，Z₃，Z₄轴的夹角α₃是已知，为90度；

沿X₃方向看，Z₃，Z₄轴的距离a₃是已知，就是臂长；

沿Z₄方向看，X₃，X₄轴的距离d₄是已知，应该为0；

因此：P_4org，局部坐标，完全是已知的，往前推一步，得到：

P²_4org =  T²₃P³_4org =  [f₁(θ₃),f₂(θ₃),f₃(θ₃),1] ^T即：

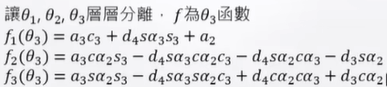
 只有θ₃是未知数。

 再拆一次：

P¹_4org =  T¹₂P²_4org =  [g₁(θ₂,θ₃) , g₂(θ₂,θ₃) , g₃(θ₂,θ₃) , 1] ^T即：

将 r = x² + y² + z²，消去θ₁

 

 

---

 

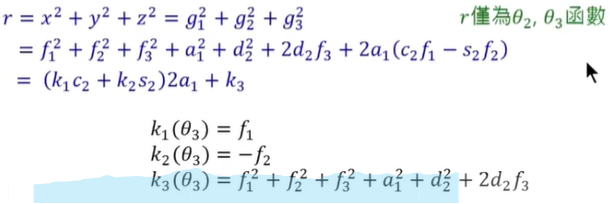
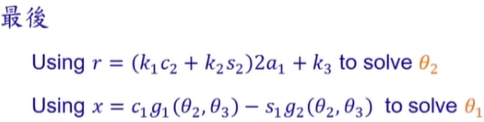
例子：

 

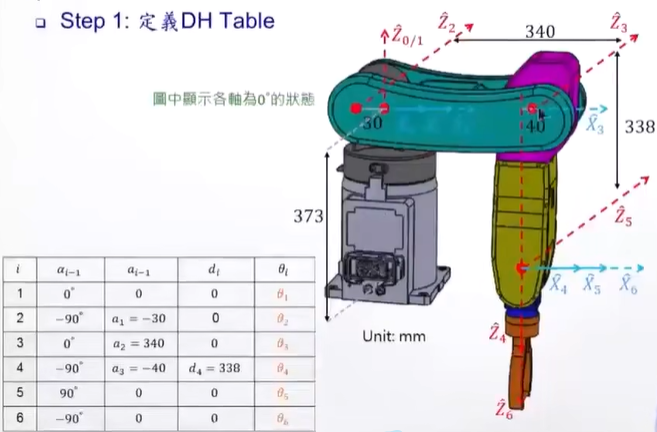
 35°，是用视觉，或者其他设计系统，计算出来的，属于已知的东西。

***θ₁貌似可以直接定35

也就是，如果知道物体在桌子的哪个位置，那么至少可以定下DH表上，最前或者最后的一个角度，消掉1到2个未知数。

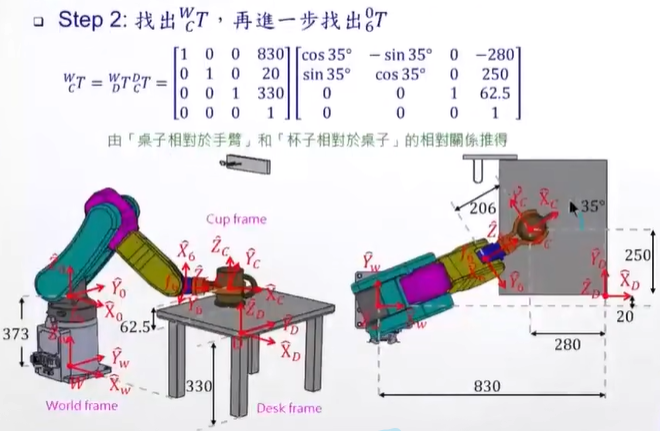
 第一步：找到T^w_c，就是世界系 - 物体中心系之间的转换。

 第二步：找到T^w₀ 、T⁶_c ， 求出T⁰₆

 T^w₀ 就是基座高度相关

 T⁶_c 就是物体中心到第6关节的转换

都是属于已知的，根据尺寸可以算出。

而T⁰₆ 的第四列，就是6系原点，相对于0系系的坐标：P⁰_6org

由于4系、6系的原点是同一个，因此P⁰_6org = P⁰_4org

第三步：计算θ₁、θ₂、θ₃

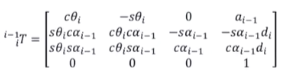
（注意到，第四列是和θ无关的）

 得到：

代入第四列，直接得到P³_4org

  第四步： θ₁、θ₂、θ₃ , 得到R⁰₃，然后根据 R⁰₆ 已知，得到R³₆