运动控制理论(2)——实践例子
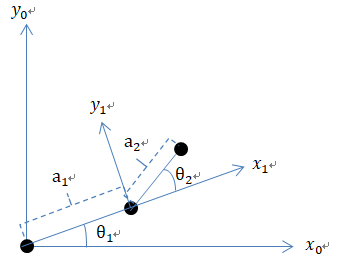
目的:要知道末端点的位置。
直观的向量法
最直接的办法,以向量相加的形式求。
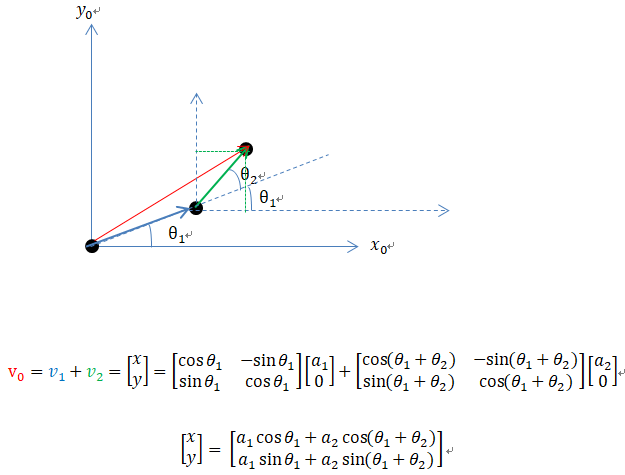
*3个向量都是参考0系构建。
坐标转换法
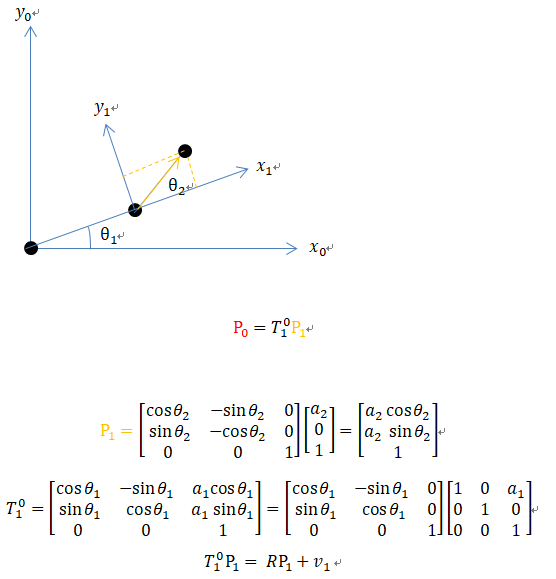
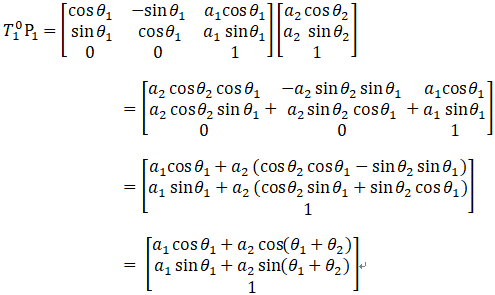
p1 是以1系下的局部坐标。
R是旋转矩阵,各列是以0系为参考的正交基。
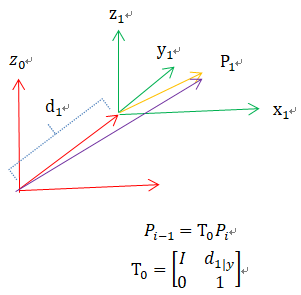
v1是平移向量,也是以0系为参考的。
合并起来变成了T。
T = R3*3t3*3 ,将旋转和平移分开两个矩阵,从左往右看,就像旋转了,然后沿旋转后的X轴平移a1,到达了第二个关节一样
多轴的例子
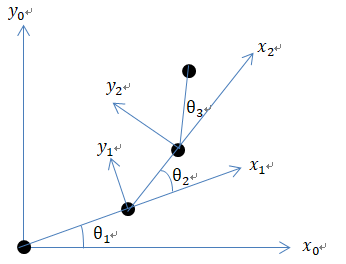
直观的向量法求解
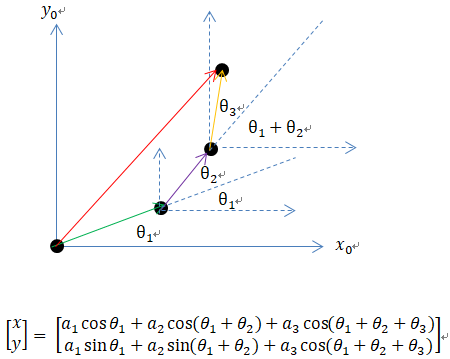
使用坐标转换的方式:
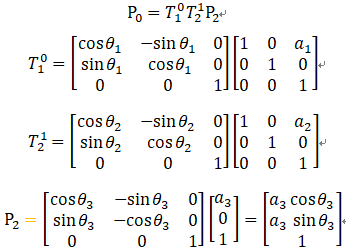

两者结果相同!
结论:
1. 以旋转、平移拆分,更容易写出不出错的T
2. 从左往右像,好像 : 旋转——沿旋转后的轴移动到下一个节点——旋转——沿旋转后的轴移动到下一个节点, 最后再乘以局部坐标。
P0 = R01 *T1* R12 * T2...Rn-1n * TnPn

如果是不是最末端,Tx3[L3,0,0] 就是一个3*3阵,第3列就是末端的坐标。
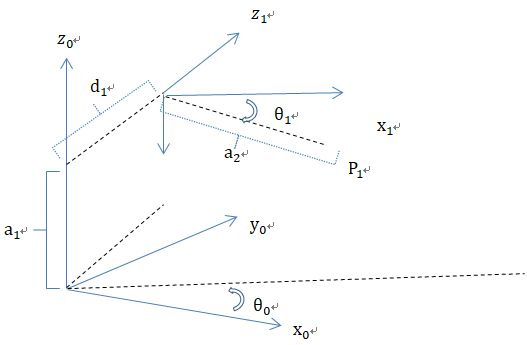
将每一步拆分,看成是后面局部坐标,转换为前面整体坐标

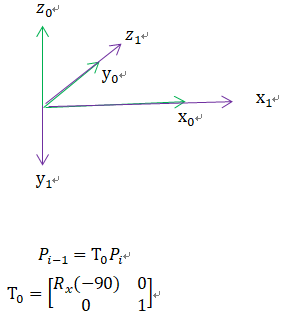

![]()


 浙公网安备 33010602011771号
浙公网安备 33010602011771号