运动控制理论（3）——机械臂控制
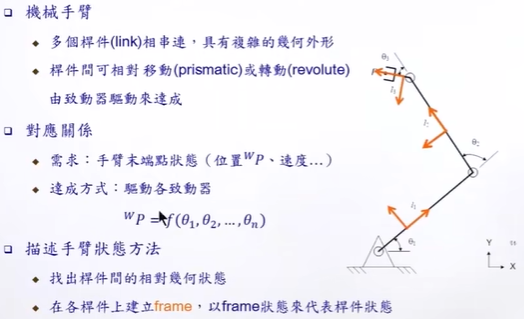
正算
已知各个关机的角度，θ1，θ2，θ3，以及臂长，求末端在世界坐标系下位置Position，三维速度。
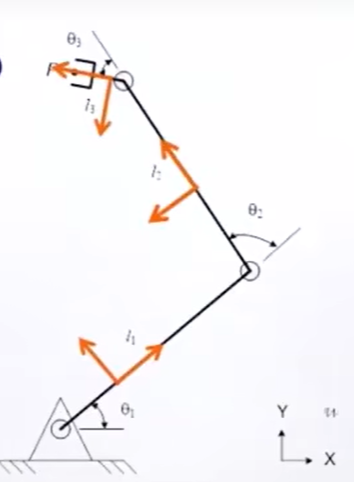
几个概念
Join：指一个关节
每个关节只能绕一个轴转rotation，或者沿一个轴伸缩translation。
Link ：刚体，jions的连接体
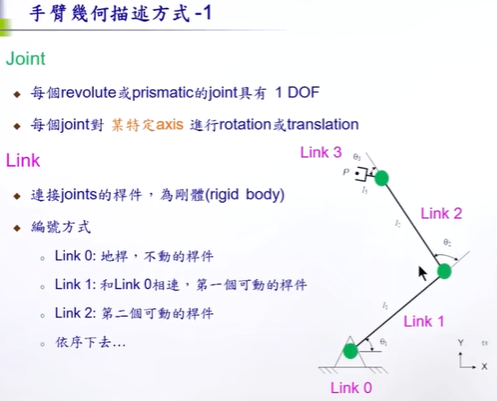
两个参数：
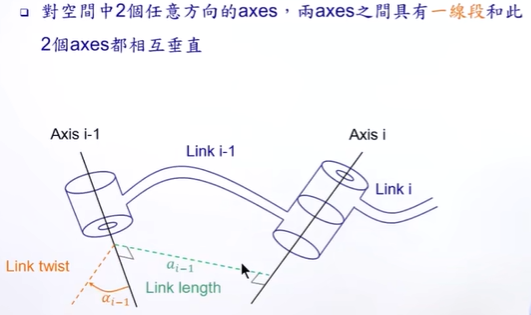
Link length：唯一连接，且垂直于空间两条线的线段，长度。
Link twist：就是两个轴的夹角（和向量夹角可能是不同的）
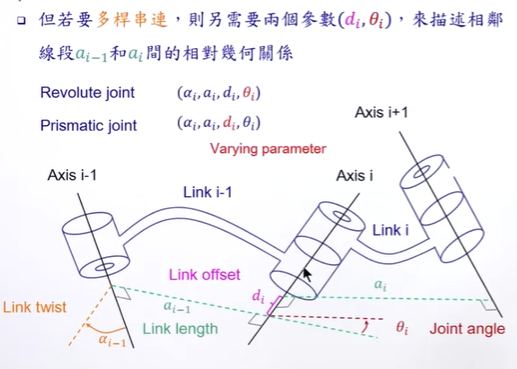
Link offset：就是di了
轴要么变di，要么变θ，（思考，如果d和θ同时变，那是不是分成两个jion好一点？？）
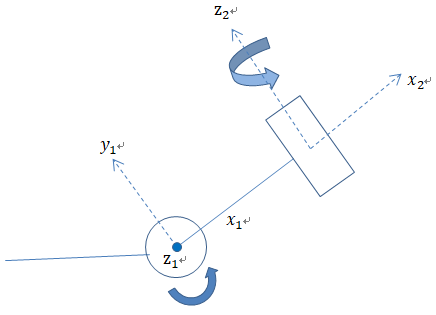
轴的定义
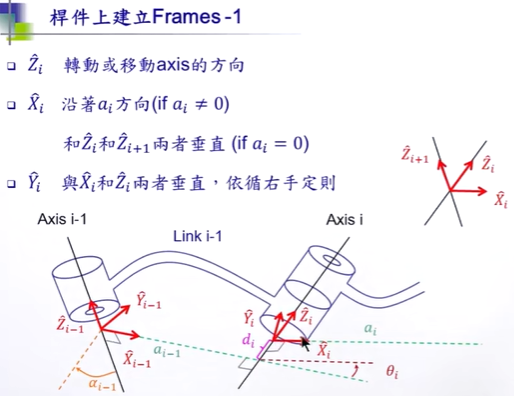
z轴沿着旋转的方向
x轴沿着Link方向，指向下一个Join。
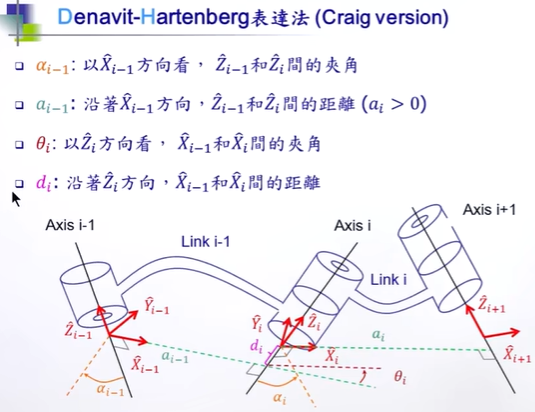
（按照定义、步骤逐步转换）
另一种方法
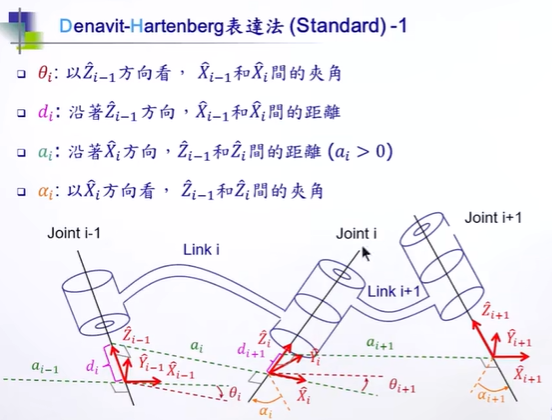
（旋转都是绕Z轴旋转）
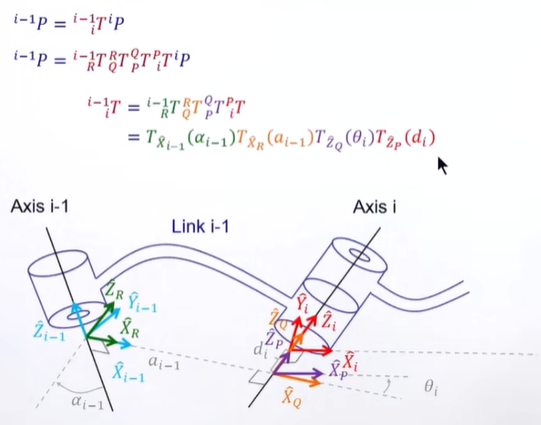
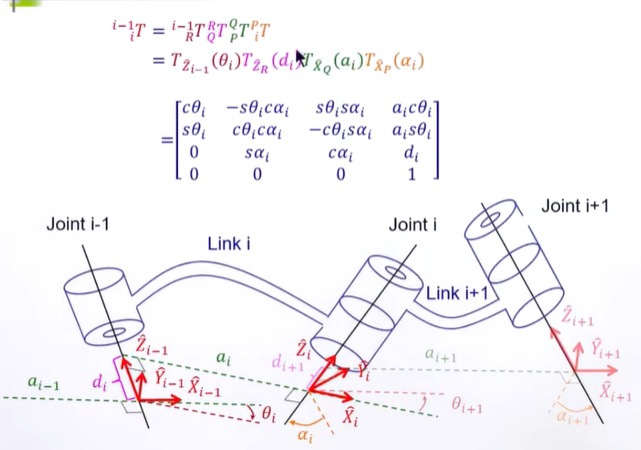
Link Transformations
以 “欧拉角” 的方式去理解，矩阵从左往右乘
1. 先绕X轴旋转：αi-1 。（这种通常是90度）
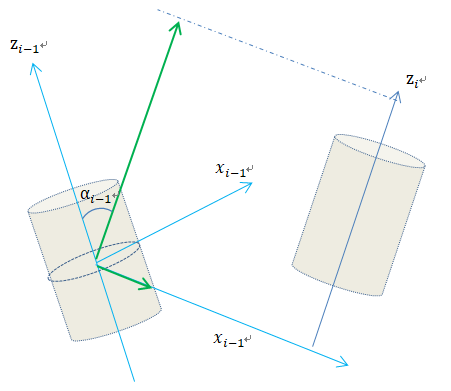
2. 然后沿着xi-1轴，移动ai-1
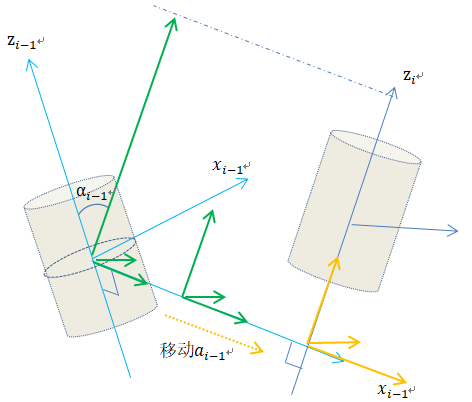
3. 然后绕旋转之后的Zi轴，旋转θi
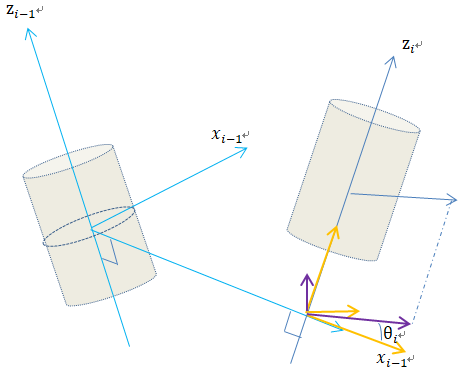
4. 然后沿旋转之后的Zi轴，移动di
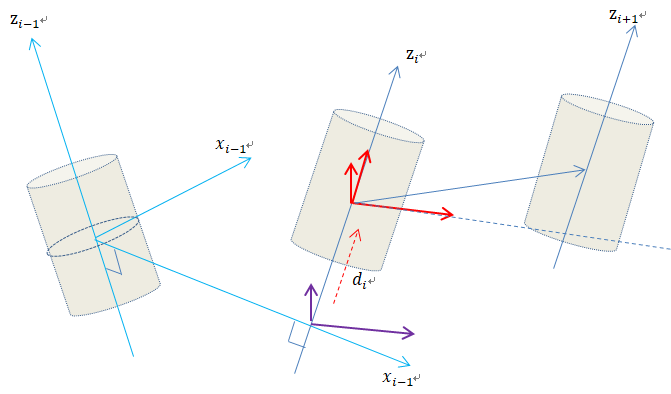
整个过程，可以表达为
Pi-1 = T i-1i Pi
Pi 是i系下的局部坐标
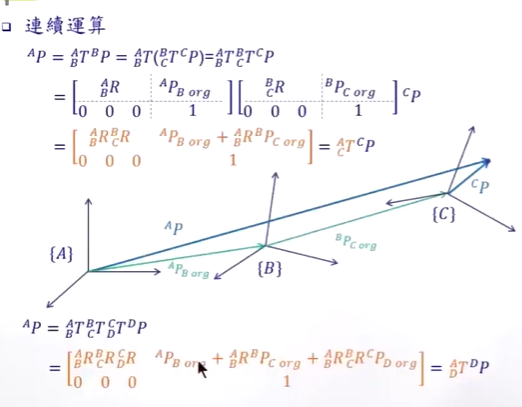
(Pi-1 = T i-1i Pi= R i-1i Pi + VB ， 用Mapping来理解，R就是旋转后的坐标基，通过Pi 线性组合成Cp （B系下）向量， Cp + VB就是B系下的向量）
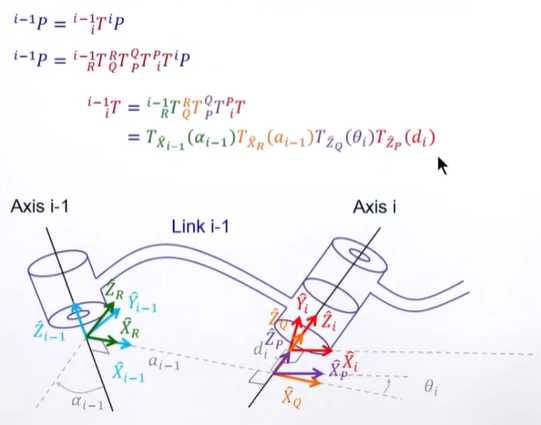
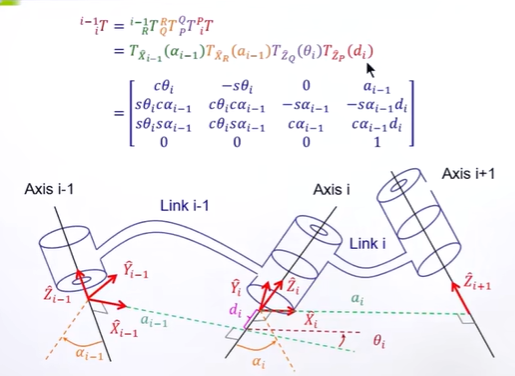
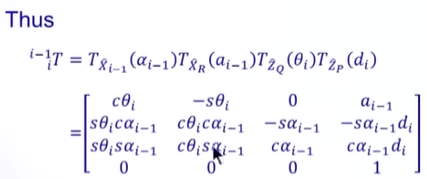
左上 3 x 3就是旋转矩阵，Mapping就是旋转后的坐标轴的向量。
右上 3 x 1就是在 i -1 系下的向量
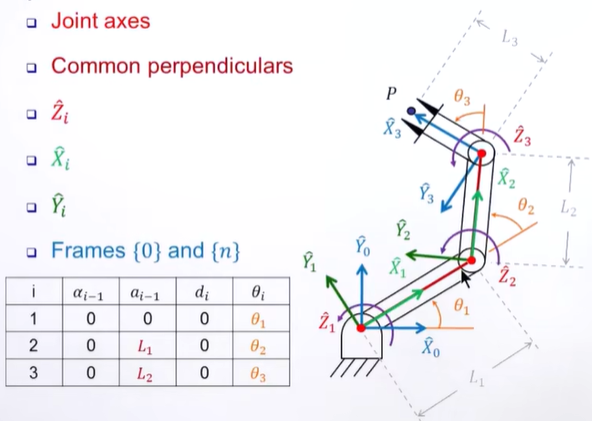
*各个X轴在同一平面内，所以d全为0
*如果是旋转join，那么z就是转轴
*如果是伸缩的join，那么z就是沿伸缩轴
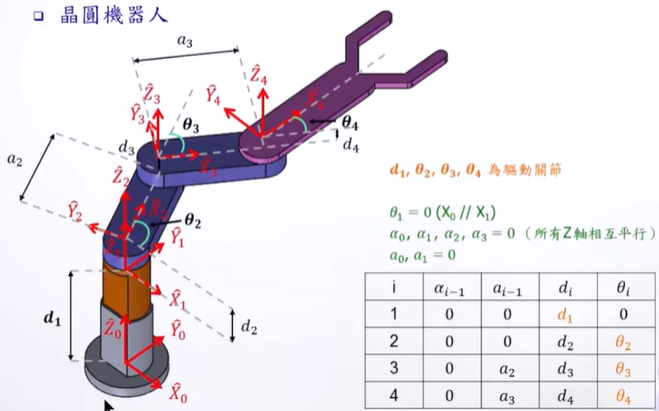
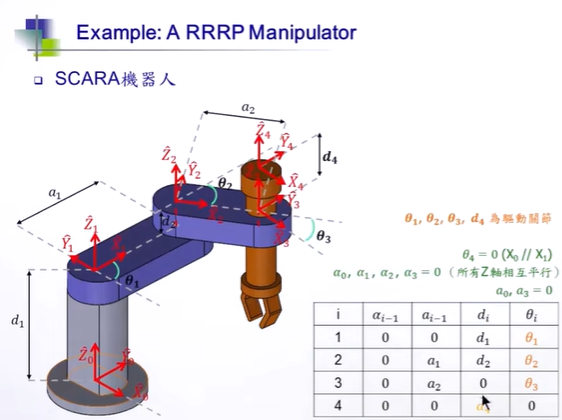
使用这种表达法比较好。
*Linki 是连接 Jioni-1与jioni的。
Xi垂直于Zi-1
*先完成在当前Jion下能完成的所有动作
使用 Standard DH
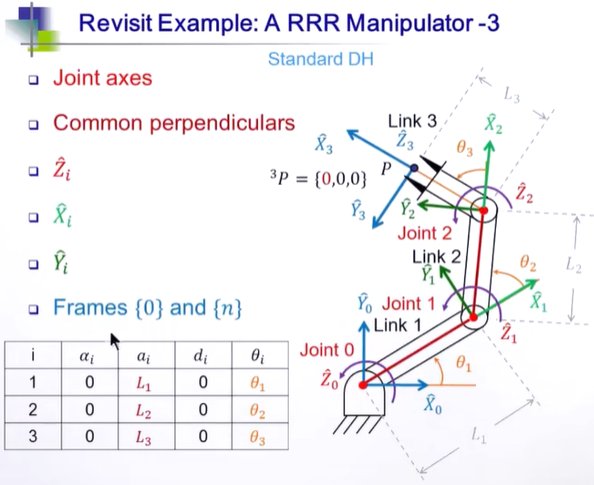
T01 p1 = R01 p1 + v
R和v合并为T。使用向量来理解， R01 p1 将 1系下的点，转为0系下的向量。
v0系下臂的向量。
思路：Mapping 和向量相加。
Craig和Standard比较
