运动控制理论（1）——刚体的运动

刚体运动本质

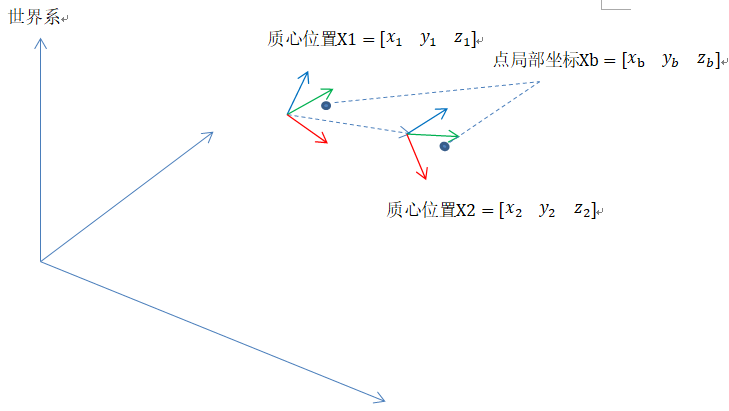
已知：

1. 质心位置X1，位置姿态C1

2. 质心位置X2，位置姿态C2

3. 点局部坐标Xb

求：【点】世界坐标

C1，理解为，世界坐标基 I （单位矩阵），旋转，得到位置1处各个箭头的向量。

C1 =  R₁ * I

C2  = R₂ * I

C1、C2可以看做是两个位置下，红、绿、蓝箭头，在世界坐标系下的向量

在位置1处，【点】的世界坐标  X_w1 =  C₁ * X_b + X₁

在位置2处，【点】的世界坐标  X_w2 =  C₂ * X_b + X₂

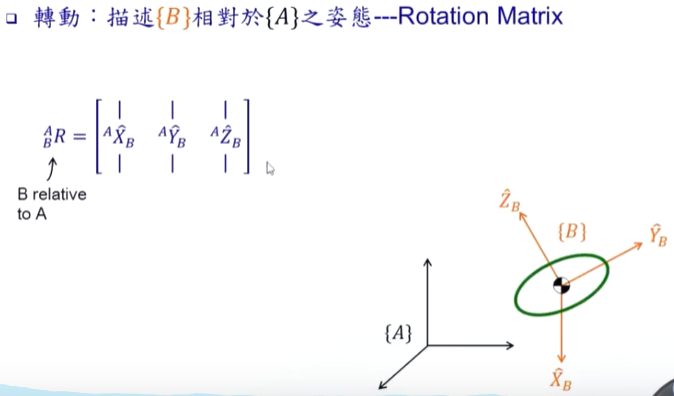
 ^AX_B ：X_B 是世界坐标系A下的向量。

 也可以这样写。

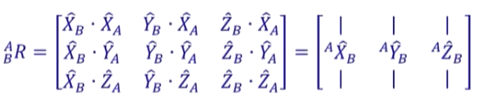
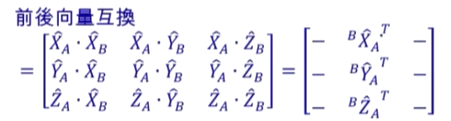
（从列的角度看，第一列，是X_B投影到A各轴上的分量，再组成一个向量，即：^AX_B）

（从行的角度看，第一行，是X_A投影到B各轴上的分量，再组成一个向量，即：^BX_A）

（注意，凡是说到向量都是列向量）

 理解：

如果只考虑旋转，不考虑平移，那么：

 X_w1 =  C₁ * X_b

 X_w2 =  C₂ * X_b

X_b =  C₁ ^-1 X_w1  = C₁^TX_w1 （单位正交矩阵， 逆等于其转置）

X_w2 = C₂ * C₁^T X_w1

X_w2 就是刚体发生旋转之后，刚体上某点，在世界坐标系下的坐标。

C₂ 则是刚体发生旋转之后，主轴在世界坐标系下的向量，也就是 [X_B, Y_B, Z_B] _3*3

假设：C₁ 则是刚体旋转前，主轴和世界坐标重合，也就是   [X_A, Y_A, Z_A] _3*3  

因此，有： R^A_B =  [X_B, Y_B, Z_B]* [X_A, Y_A, Z_A]^T

即：X_w2 = R X_w1

如果是有世界坐标，没有更大的坐标，那么：I =   [X_A, Y_A, Z_A] _3*3  ， X_b = X_w1 ，因此有：X_w2 = R^A_B X_b =  C₂X_b

---

 

 

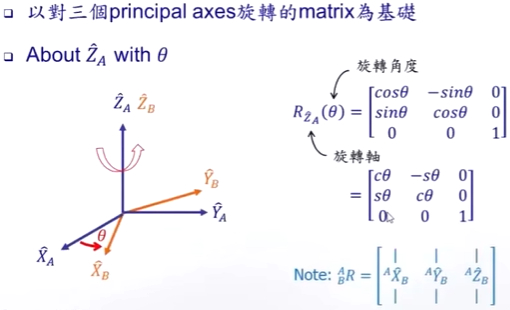
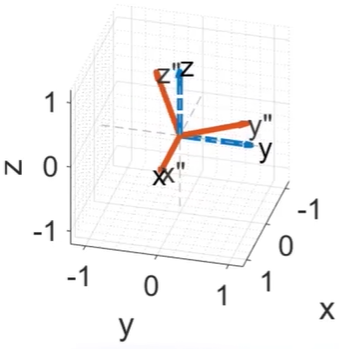
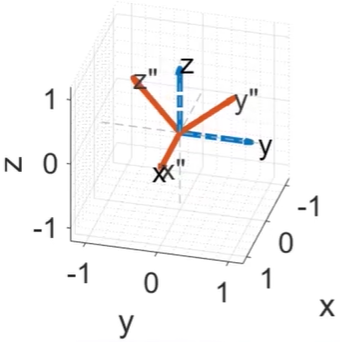
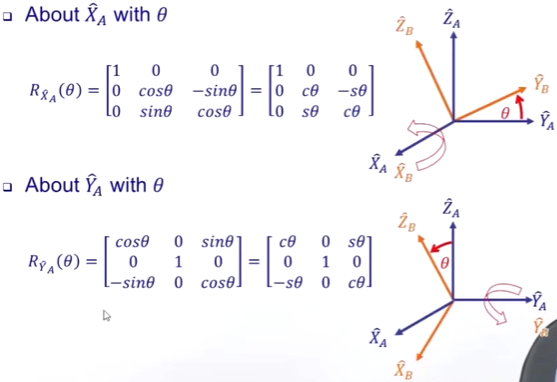
选择具有 not Commutable (不可交换顺序)的性质

---

 旋转有两种方式：

1.  Fixed angles。( 旋转总是绕固定的 “ 世界坐标”下的轴 )

（注意，顺序是先绕X，再绕Y，再绕Z，矩阵的顺序，是从右到左，也就是向左乘）

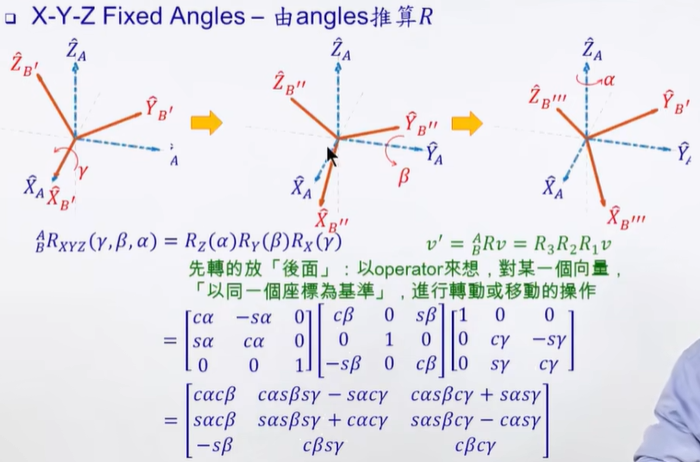
（注意R的下标，对比欧拉转法）

（注意，先绕X轴转的，放到后面！！！）

 

 （之所以用Atan2，不用Atan，是因为 Atan输入一个数字，Atan(1) , 只能得到45度（0~180），而Atan2(-1,-1)和Atan2(1,1)，结果是45度和135度）

（疑惑疑惑：Fixed Angle怎么和其他书上的欧拉角是一样的？？）

（看下面，顺序不一样！）

2. Euler angles。（欧拉角） 旋转开始时，载体轴和世界轴重合，第一次旋转绕世界轴，载体轴都是一样的；之后的旋转，载体轴和世界轴不重合，然后都是绕载体轴来旋转了。

 （注意，顺序是先绕Z轴转，再绕Y’轴转，再绕X’轴转，但是矩阵的顺序，是从左到右，也就是向右成）

 这里要和X_b 对 R^A_B进行线性组合的思维需要有区分。

^BP 或 X_b，得看成是另一个坐标系下的坐标，而非想象为载体坐标系。

固定坐标系（Fixed angles）的左乘相当于给基准坐标系的向量进行齐次变换，坐标系没有发生变化，由当前向量经过运动后得到最终向量相对于基准坐标系的位置（已知向量相对于初始坐标系位置），数学表达符合左乘；

（向量动，世界坐标不动）

旋转（运动）（Euler angles）坐标系的右乘相当于将整个坐标系进行齐次变换，但是向量只有在空间相对于最终变换坐标系的位置已知（已知向量相对于最终坐标系的位置），需要得到向量相对于最初的基准坐标系的的位置，相当于求反解，符合数学表达右乘。

（向量不动，相当于载体坐标是固定的，只有世界坐标系动，所以要求反，就要右乘）

 结论：给的α，β，γ，用fix angle和 eular angle，算出的R是一样的！！！！但是顺序一定要对应！！！

 (可以看到，使用fix angle，先绕X60，再绕Y30   = eular angle 先绕Y30，再绕X60)

参考：https://blog.csdn.net/chen_mp/article/details/133365293

（欧拉角 和 固定角，仅仅是理解角度不同，但是从公式入手，是完全相同的！欧拉角的ZXY（312）等价于固定角的 YXZ（213）， 都是 T = Rz Rx Ry）

（并且，再世界坐标系下，欧拉角按照312转，xyz对应载体坐标系的“右前上”，转换后的坐标为“ENZ”）

 

---

 

特殊的欧拉转发

使用ZYZ

  

 (任何的旋转矩阵，可以用任何的方式拆解！！)

 无论如何，反正下一次旋转绕的轴，和上一次不一样，那么就有 3 * 2 * 2  = 12 种！

---

 

大一统，旋转向量

绕某一个单位向量，转一个角度

 

---

 

旋转和移动

P_A = R^A_BP_b + T

其中R _3*3,  T_3*1

假设P_b是P点局部坐标系下的向量，并且局部坐标系与世界坐标系没有旋转关系。

所以P_b也是世界坐标系下的向量

 求P点在世界坐标系下的向量，根据向量相加法则，有如上公式。

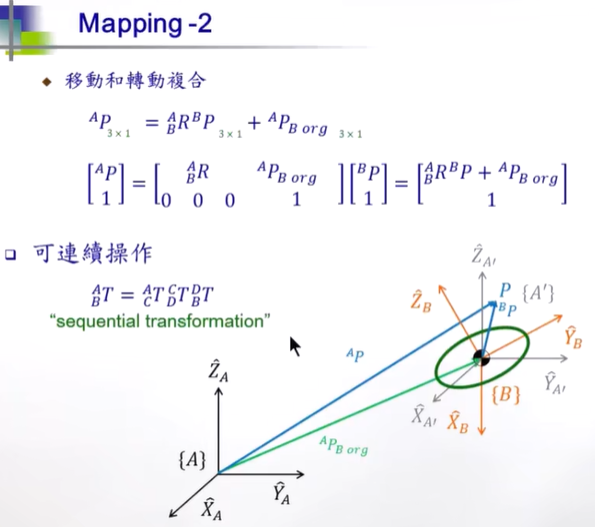
R^A_BP_b 的作用，正是将向量P_b转换为世界坐标系下的向量 ， 再与世界坐标系下的向量P_Borg进行向量加运算

P_b是橙色坐标系下的坐标

R^A_B 既是旋转矩阵，也是世界坐标系下的单位正交向量组，只是旋转了不和世界坐标系的轴重合

---

 

 从Fixed  Angle旋转的角度来看，P_b一开始就不是局部坐标系下的坐标了，而是世界坐标系下的坐标。

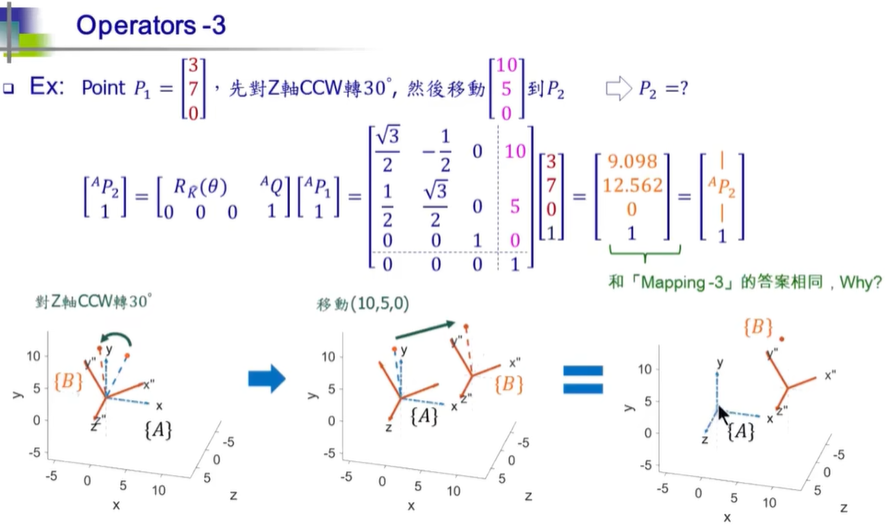
 然而，P_b却是一样的，因此，从哪个角度看待P_b很重要！

一个是点不动，世界在动；一个是世界不动，点在动。

区别是：

1. 如果知道局部坐标轴向量，P_b就是局部坐标系下的坐标。（不会既知道坐标基向量，也知道P在世界坐标系下的坐标，不然就不用求了吧）。RP_b 起到一个还原到世界坐标系下得向量作用，就是mapping思维。

2. 如果只知道动作（operate），旋转多少度，那么P_b就是世界坐标系下的向量。RP_b 起到变换的作用，就是operate的意思。

---

 

将世界，起一个别名Frame

P_A = RP_b + T

如果使用Frame动，点不动，求点在Frame变成Frame2时，P在Frame2下的坐标。

 

---

 

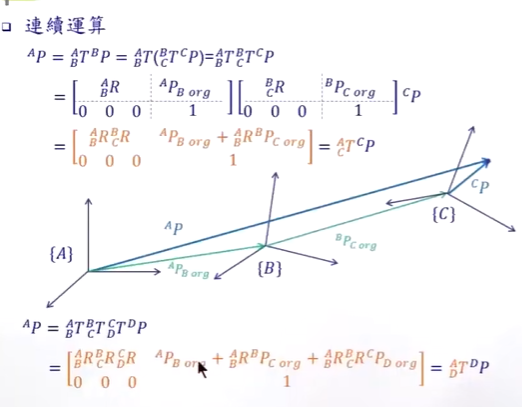
 P_c在A系下的表达求解

可以看到，位移向量也是全部转到A系下的位移向量

---

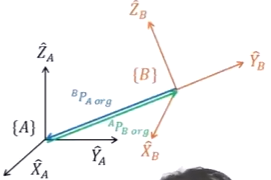
 ^AP_Borg 是相对于A系下的向量。

^BP_Aorg 是相对于B系下的向量。

 

---

 

左乘右乘

（重点）

1. 以Operate的角度理解：

类似于Fix Angle，一开始是，B系和A系重合，T^A_B = I ， v是刚开始时A系下的一个向量

随后，B绕A进行旋转变换。

2. 以Mapping的角度来理解：

类似于Euler angles，一开始P_B 就是最后一个载体坐标系下的坐标。

 所以，这里区分v和P_B

总结：如果使用Euler angles， P_B一开始是载体坐标；使用Fix Angle，P_B一开始是世界坐标。

 

---

 

欧拉角使用右乘的方式，右边矩阵各列，是相对于前面矩阵构成的局部坐标系下的载体坐标，其分量对左边矩阵各列进行线性组合。

而左边矩阵各列，又是世界坐标系下的向量，线性组合的结果自然也是世界坐标系下向量。

因此右乘旋转矩阵，是以自身为参考进行旋转的，最终得到旋转后各坐标轴在世界坐标系下的向量。