图优化基础:极大似然估计
设有观测方程:
Zi = g(xi) + vi
xi为待求量,vi为观测噪声,服从 vi ~ N(0,Σ)
等价于 zi ~ N(g(xi) , Σ)
* 这里Z,x,v都是多维向量,而∑是协方差阵。
贝叶斯估计: p(x) * p(z | x ) = p(z) * p(x|z) = p(x,z)
*人话 : x与z同时达到某值的概率 = x达到某值的概率 * x达到某值的条件下,z达到某值的概率
p(x|z) = p(z|x) * p(x) / p(z)
*人话:p(x|z) : 已知z达到某值,x发生的概率 ;
理解:
p(x|z) ∝ p(z | x) * p(x)
*∝是“正比于” 的意思。因为z是已经发生了,所以p(z)可以认为1,要比较左右关系,不需要考虑p(z)
* 假设x的解是x^,概率是p(x^|z)。可以肯定,p(x^|z)的概率比 p(x1|z) 、p(x2|z)、 p(x3|z) 都大
那么假设 p(x|z) = f(x,z),只要找出哪个x,使得 p(x|z)最大。
由于有∝ 的关系,等同于找到:
x = argmax( p(x|z) ) = argmax[ p(z | x) * p(x) ] : 极大后验估计
人话:因为 p(x)又是不知道的 ,如果知道x的概率分布函数,那直接找概率最大时对应那个x就行了,不用估计了。
所以,只能退而求次,去找:
x = argmax( p(x|z) ) ≈ argmax p(z | x) : 极大似然估计
*人话 :能不能理解为,极大似然估计与极大后验估计,在参数先验概率p(x)未知时,是等价的?
p( x | z)又叫【后验】:z是果, x是因。知果求因。(观察值是果,待求量是因,类似于先有那样东西的存在,才能被观测到)
p(z | x) 又叫【似然】:知果求因。
p(x)又叫【先验】
先验后验: https://www.cnblogs.com/pylblog/p/16937997.html
现在考虑 p(z | x) 到底是怎样一个函数。 结论是: zi ~ N(g(xi) , Σ)
*人话:因为z已经是发生的了,所以p(z)=1。 那 zi ~ N(g(xi) , Σ) 只能是p(z | x)
p(z | x) = f (g(xi)) , f是高斯分布函数,代入求极大值:
https://www.cnblogs.com/pylblog/p/16937997.html
* 协方差矩阵的逆,∑-1又叫【权矩阵】、【信息矩阵】解 AT∑-1A x= AT∑-1b ,得到x



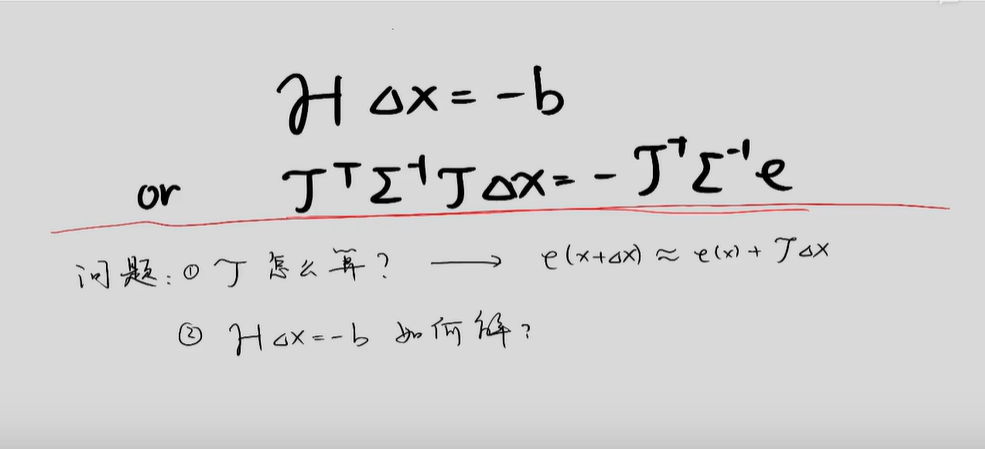




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 分享一个免费、快速、无限量使用的满血 DeepSeek R1 模型,支持深度思考和联网搜索!
· 基于 Docker 搭建 FRP 内网穿透开源项目(很简单哒)
· ollama系列01:轻松3步本地部署deepseek,普通电脑可用
· 25岁的心里话
· 按钮权限的设计及实现