组合导航原理（九）——误差微分方程

 

令：

x^{^} = x + δx

（测量平差书上，是x^{^} = x₀ + δx，将x^{^} 认为是真值）

x是真值

δx是误差

x^{^} 是测量值

如果放到泰勒展开式，可以得到：

f(x) = f(x₀) + df(x) / dx * (  x  - x₀ )  

当x₀ = x^{^}

那么：

f(x) = f(x^{^}) + df(x) / dx * ( x  - x^{^})  = f(x₀) + df(x) / dx * -δx

解得：-δx 

 x^{^} + -δx = x

刚好是优化的结果！

---

 

以 ωⁿ_ie = [ ω_e * cosφ ，0 ， -ω_esinφ ] ^T

φ^{^} = φ + δφ

注意，这里不是泰勒展开：（书上的所有地方，都不是泰勒展开！！！！）

 ωⁿ_ie^{^}(1) =  ω_e * cos(φ + δφ)

               =  ω_e * (cos(φ) cos(δφ) - sin(φ)sin(δφ)  )

                ≈ ω_e * cos(φ)  - ω_esin(φ) δφ 

 δφ  = ....（目的1）

暂时理解：要将所有的误差项，作为待求量，或者系统状态。卡尔曼滤波就是估计最优的δ， 最优（位置，速度，姿态） =  δ （位置，速度，姿态）+  测量值（位置，速度，姿态）

例如：φ就是维度，是位置分量

 δx_k = Fδx_k-1 + ω_k-1 ( 用上一时刻的误差，估计下一时刻的误差  )

---

姿态微分方程

 旋转矩阵Cⁿ_b，对应的欧拉角为 [ Φ， θ，ψ ]，假设有误差为 ϕ = [ ϕ_N , ϕ_E,  ϕ_D]^T

 那么，但是欧拉角是不可以相加的，[ Φ+ϕ_N， θ+ϕ_E，ψ+ ϕ_D]^T无意义

假设：

（1）最终要求的系为n^系（别名p系），那么有：

 （2）若ϕ = [ ϕ_N , ϕ_E,  ϕ_D]^T，是从p系转到n系（未改正的n系）得： ϕⁿ = [ ϕ_N , ϕ_E,  ϕ_D]^T

因此：

（掉过来n转p是 -ϕx ）

 

 (Cⁿ_b ) ' = Cⁿ_b (ω^b_nb X )

ω^b_nb X = ω^b_ni X + ω^b_ib X =   - ω^b_in X + ω^b_ib X = ω^b_ib X - ω^b_in X

 (Cⁿ_b ) ' = Cⁿ_b (ω^b_ib X - ω^b_in X )

             = Cⁿ_b  ω^b_ib X - Cⁿ_b ω^b_in X

重要公式：V^R_X  = C^R_b ( V^b_X )C^b_R

(Cⁿ_b ) ' = Cⁿ_b  ω^b_ib X - Cⁿ_b ω^b_in X

　　　 = Cⁿ_b  ω^b_ib X - Cⁿ_b   C^b_n  (ωⁿ_inX) Cⁿ_b

            =  Cⁿ_b  ω^b_ib X -  (ωⁿ_inX) Cⁿ_b

ωⁿ_in = ωⁿ_ie + ωⁿ_en

 

---

 

 

 

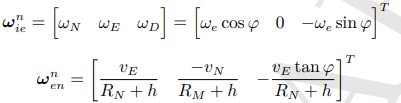
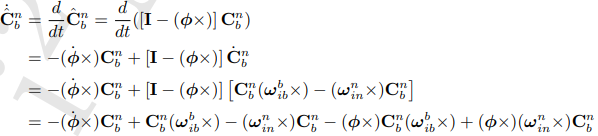
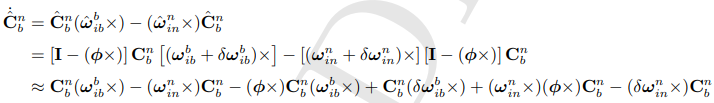
忽略二阶小（小值 * 小值=  0）的情况下， 两个式子相等：

 

 

 

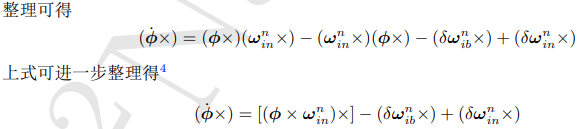
 误差，或者扰动项ϕⁿ 的导数：

 

ϕ‘ =  - ωⁿ_in X ϕ + δωⁿ_in  -  δωⁿ_ib

  问题：为什么要求导？直接表达ϕⁿ 不好吗？

Φ = ∫ Φ' dt

---

 

δr_N 是 在n系下，由于纬度φ误差δφ，造成的n系坐标在N轴方向上的误差

因此：

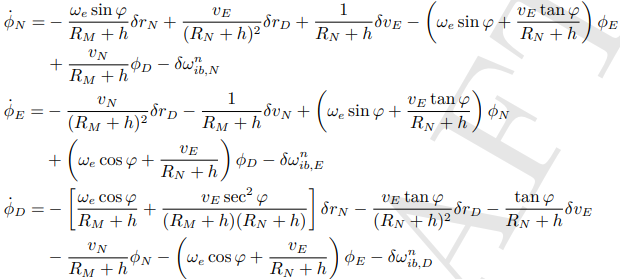
 ωⁿ_in = ωⁿ_ie + ωⁿ_en

 

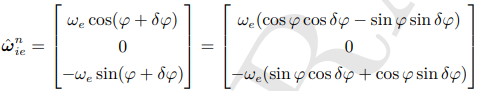
又δφ（纬度误差）为小值，因此 δωⁿ_ie = (ωⁿ_ie)^{^}- ωⁿ_ie

 

同理，求δωⁿ_en

 

 

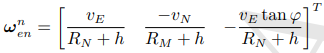
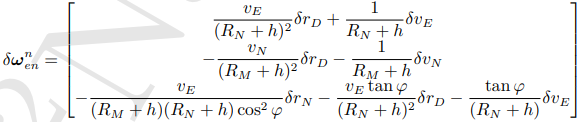
  δωⁿ_in =  δωⁿ_ie - δωⁿ_en

  δωⁿ_ib

但是，IMU输出的是Δθ = ∫ ωbib

记得有公式：ωⁿ_ib X =  Cⁿ_b  ω^b_ibCⁿ_b 

而  ( ωⁿ_ib X  +  δωⁿ_ib X)  =  Cⁿ_b  （ ω^b_ib  X +  δω^b_ib X）Cⁿ_b

所以：δωⁿ_ib X =  Cⁿ_b  δω^b_ibCⁿ_b  ， IMU的角速度误差δω^b_ib  ，可以转化为投影在n系下的角速度误差δωⁿ_ib 

δω^b_ib = [ δω^b_{ib,N ,} δω^b_ib,E  δω^b_ib,D  ]^T

必须注意的地方：

δω^b_ib = [ δω^b_{ib,N ,} δω^b_ib,E  δω^b_ib,D  ]^T 的顺序 

 

---

 

假设有如下定义：

 

b系的 [ X,  Y , Z ]对应方向 [右，前，上] 

当 Cⁿ_b = I时，[ X,  Y , Z ] 对准n系的 [ E, N , Z ]

Δθ 为小量时， C^b(k)_b(k+1)= I + [ Δθ,  Δγ , Δψ  ]^T ， Δθ 为小量时绕哪个先都无所谓，