组合导航原理（七）——位姿算法更新总结

IMU输出的是：

t时刻的角度增量：Δθ(t) = ∫ w^b_ib(τ)dτ

t时刻的速度增量：Δv(t)= ∫ f^b (τ)dτ

t时刻的增量，是相对于t-1时刻而言，并不是初始时刻，这个要特别注意。

 

而角度增量Δθ(t)、速度增量Δv(t)中，抹掉了很多信息，比如：

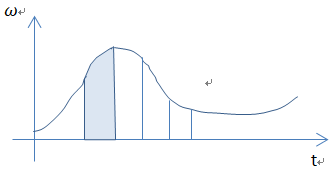
输出的蓝色的面积，但是曲线细节没有展现。

以w^b_ib为例，因为w^b_ib 是时变的，也就是三轴角速度不是一个定值，那么【旋转向量】就是飘忽不定的。

所以如果直接拿Δθ做旋转，相当于肯定了w^b_ib 为定值_，从而【旋转(轴)向量】是固定的，从而产生了误差。

（猜测：单轴旋转了一点a，再旋转回去b，对于IMU输出，就是Δθ = a - b，但是旋转本身，是不能通过角度相加的）

为了消除这个误差，要将w^b_ib 引出，找到它与【等效旋转向量】的关系，从而：

【等效旋转向量】  Φ(t) = F (Δθ, w^b_ib(t)) 形成一个复合函数，这个复合函数中，IMU的输出Δθ则变成一个常量值，解出【等效旋转向量】，再用来进行旋转。

（引出w^b_ib  对【角度增量】的作用，再假设w^b_ib(t) = f(Δθ_k-2 , Δθ_k-1 ,Δθ_k )，就可以解除Φ(t)的复合形式，最终解得【等效旋转向量】）

（【旋转向量】我认为是一个概念，而【等效旋转向量】是实际具体干活用的对象）

 

至于速度也是同一个道理：

所以如果直接拿Δv做位移，那么就肯定了【加速度】是恒定的。

为了消除这个误差，要将f^b引出，找到它与【等效速度增量】的关系，从而：

【等效速度增量】 =   F (Δv, f^b(t))形成一个复合函数，这个复合函数中，IMU的输出Δv则变成一个常量值， 解出【等效速度增量】，再用来进行速度计算，从而得到位移。

（引出f^b  对【速度增量】的作用，再假设f^b (t)= f(Δv_k-2 , Δv_k-1 ,Δv_k )，就可以解除复合形式，最终解得【等效速度增量】）

（【速度增量】我认为是一个概念，而【等效速度增量】是实际具体干活用的对象）