哥氏定理
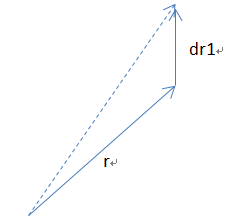
空间某一个向量r,打算增加dr1
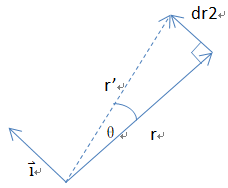
同时发生旋转,增加dr2
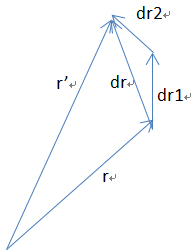
最后变为r’
那么r的变化速度,可以对dr进行微分
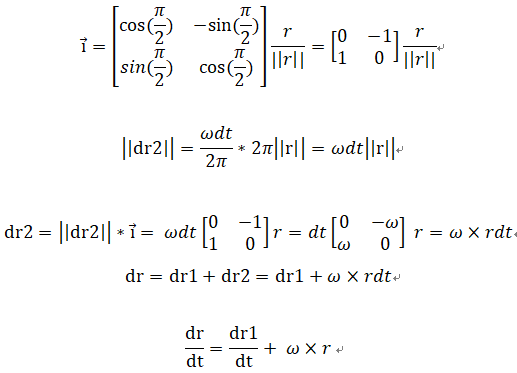
(1)在θ为微小值得时候,可以认为dr2⊥r,dr2单位化对应的向量为i
(2)在θ为微小值得时候,可以认为dr2 的长度,就是转过的圆弧的长度
(3)观察到 ω X r * dt,就是一个向量,沿着旋转的切方向,经过dt后产生的分量
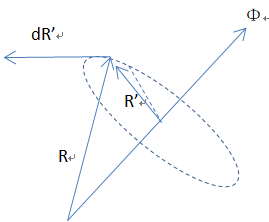
(1)按照上面的理解,将R分解,分别计算旋转带来的增量,再合并,还是ω X R* dt
速度微分方程

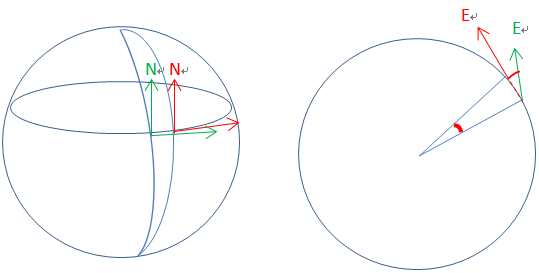
对哥氏方程的理解
dr / dt |i : 在太空中观测地球上的向量的变化
dr / dt |b :在地球观测向量的变化
ωie X r :地球自转使得向量发生的变化
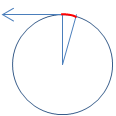
弧长 = ω * Δt / 2Π * 2Π R = ω * Δt * R
速度 = ω * Δt * R / Δt = ω * R

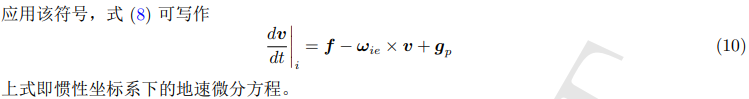
ri : 是惯性系下的向量,因此长度至少是地球的半径
ωie X (ωie X r):理解为向心力(离心力)
助记:
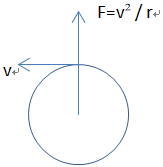
v = ω * R
所以F = ω * ω * R

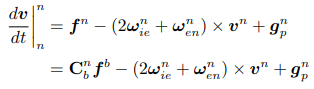
fb:比力,IMU能直接测出,要转换为fn
gnp:算出当地的重力加速度gp = [0,0,gnp],应该是很近似的,只有Z方向有
陀螺和加速度计的测量值(增量输出)
Δθk = ∫ ωbib(τ)dτ
Δvk = ∫ fb(τ)dτ
想要得到的是当前时刻的速度 Vnk
对:
dv / dt|nn = Cnbfb - (2ωnie + ωnen) X vn + gnp
积分:
Vnk = Vnk-1 + ∫ Cnb(t) fb(t) dt + ∫ [ gnp(t) - (2ωnie(t) + ωnen(t)) X Vnk] dt
= Vnk-1 + ΔVnf,k + ΔVng/cor,k
注意:Vnk 是在导航系下运动的速度,并不是IMU输出,IMU输出的是各轴的速度增量
f比力;g/cor 重力与哥氏加速度。
ΔVnf,k = ∫ Cnb(t) fb(t) dt
ΔVng/cor,k = ∫ [ gnp(t) - (2ωnie(t) + ωnen(t)) X Vnk] dt
gnp(t) - (2ωnie(t) + ωnen(t)) X Vnk
gnp(t) 和位置有关,在 tk-1 ~ tk 变化不大 。
ωnie(t) 是常值,地球自转相关。
ωnen (t) 是微小值,和位置、速度、地球半径有关。
但是,Vnk 又是要求的,那就变成先又鸡还是先又蛋的问题?
答案:Vnk 可以用近似的来代替
令:
Vnk ≈ Vnk-1/2 = Vnk-1 + 1 / 2 *( Vnk-1 - Vnk-2 )
那么:
agc≈ agc,k-1/2 = [ gnp(t) - (2ωnie(t) + ωnen(t)) X Vnk-1/2]
思考:gnp(t) 、 ωnen(t) 能不能用上一个位置(纬度,大地高)来代替。
最终: ΔVng/cor,k ≈ agc,k-1/2 Δt
ΔVnf,k = ∫ Cnb(t) fb(t) dt
ΔVnf,k = ∫ Cn(t)n(k-1) Cn(k-1)b(k-1) Cb(k-1)b(t) fb(t)dt
Cn(k-1)b(k-1) :已知
Cn(t)n(k-1) : tk-1 ~ tk 变化不大
( tk-1 ~ tk 在地表移动110km,n系才旋转1°)
Cn(t)n(k-1) ≈ 1 / 2 * (Cn(k)n(k-1) + Cn(k-1)n(k-1)) = 1 / 2 * (Cn(k)n(k-1) + I)
是一个常值。
Cb(k-1)b(t) : tk-1 ~ tk 变化快。
那么:
ΔVnf,k ≈ Cn(t)n(k-1) Cn(k-1)b(k-1) ∫Cb(k-1)b(t) dt
= 1 / 2 * (Cn(k)n(k-1) + I) Cn(k-1)b(k-1) ∫Cb(k-1)b(t) fb(t)dt
Cn(k-1)b(k-1) : 上一个时刻已算
Cn(k)n(k-1) ≈ I - ( ζn(k-1)n(k) X)
ζn(k-1)n(k) n系从 tk-1 转到 tk 的角度增量(向量)
ζn(k-1)n(k) ≈ ∫ ωn(k-1)n(t) dt
ωn(k-1)n(t) t时的n系,相对于k-1时的角速度
ωn(k-1)n(t) = ωn(k-1)i + ω in(t)
ζn(k-1)n(k) ≈ [ ωn(k-1)i + ω in(t)] Δt
又
ωn(k-1),i 在k-1瞬间,可以认为i系和n系固结,所以ωn(k-1),i = 0 (?????)
ω i,n(t) = ω i,e(t) + ω e,n(t)
ω i,e(t) = [ ω e cosφ(t), 0 ,-ω e sinφ(t)] T
ω e,n(t) = [ vE/(RN + h) , -vN/(RM + h) , -vEtanφ/(RN + h) ]T
RM = a(1-e²) / sqrt( 1 - e²sin²φ)³
RN = a / sqrt( 1 - e²sin²φ)
φ 为纬度
vE载体向东移动速度
vN载体向北移动速度。
a为地球长半轴,6378137.0m。
RM和 RN分别为子午圈和卯酉圈半径。
速度近似:Vnk ≈ Vnk-1/2 = [ vN,vE, vz ] T = Vnk-1 + 1 / 2 *( Vnk-1 - Vnk-2 )
纬度近似:φ (t) = φk-1 + 1 / 2 *( φk-1 - φk-2 )
ΔVb(k-1)f,k = ∫Cb(k-1)b(t) fb(t)dt
C b(k-1)b(t) = I + sin ||Φ(t)|| / ||Φ(t)|| * Φ(t)X + ( 1 - cos ||Φ(t)|| ) / ||Φ(t)||² * Φ(t)X Φ(t)X
Φ(t) 表示从 tk-1时刻,到t ∈[ tk-1,tk]的【等效旋转矢量】
由于 Φ(t) 是微小量,因此:
C b(k-1)b(t) ≈ I + Φ(t)X
Φ(t) = Δθ(t),如果t = tk,那么就刚好是陀螺的输出了
(角增量 = 旋转向量在之前已经证明过了)
C b(k-1)b(t) ≈ I + Δθ(t)X
Δθ(t) = ∫ ωbib(τ) dτ
看到这里,马上就可以想起四元素更新姿态,假设ωbib(τ) = F(Δθk-2,Δθk-1,Δθk)
ΔV(t) = ∫ fb(τ)dτ
同理, 假设fb(τ) = F(ΔVk-2,ΔVk-1,ΔVk)
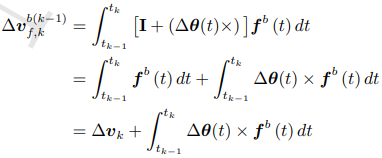
其中:
ΔVk 就是tk-1~tk的IMU输出的速度增量
可以看见,ΔVk 相对于 Vnk , 包了很多层,才到导航系的速度
(Vnk(ΔVnf,k(ΔVb(k-1)f,k(ΔVk))))
最后,将 Δθ(t)、ΔV(t)方程代到式子中,再进行积分计算
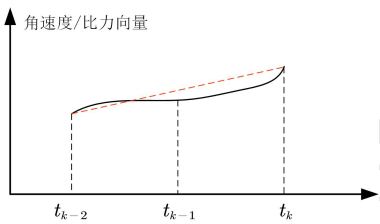
假设是双子样算法:
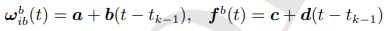
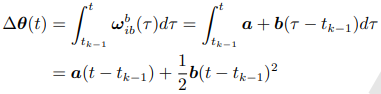
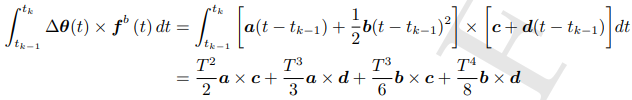
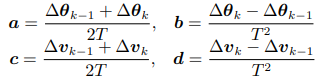
最终:
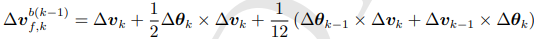
(可以看到,比力造成的速度增量,是IMU输出的速度增量Δv,加后面一堆补偿项)
整理:
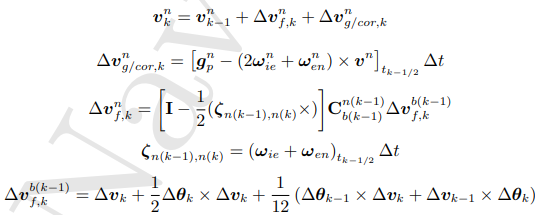
计算出【等效速度】 Vnk = [vN,vE,vD ]T后,就可以进行位置计算
载体的位置可用大地坐标(纬度 φ、经度 λ 和椭球高 h)来表示。位置随时间的变化可用下面一组 微分方程来描述:
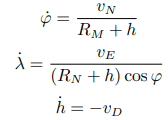
(要记得,书上的n系是向下为正方向的,估计是因为比力向下是正输出,所以n系也写成向下为正了)
更新步骤:
1 . 先更新h
2. 再更新φ(纬度)
3. 最后更新λ(经度)



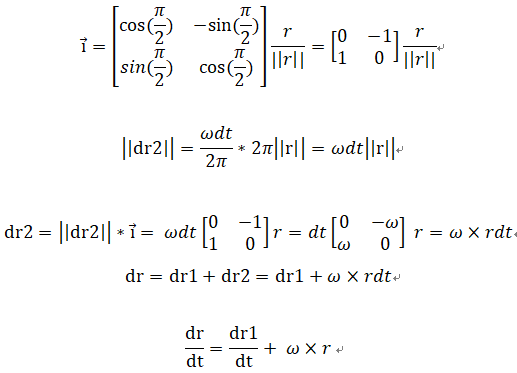




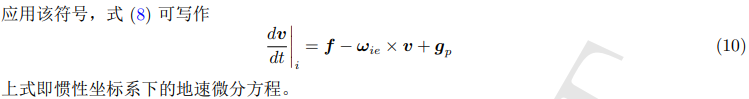


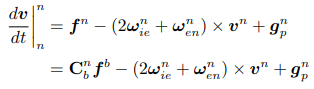
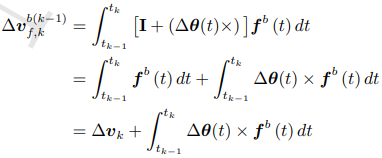
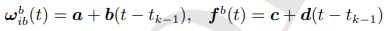
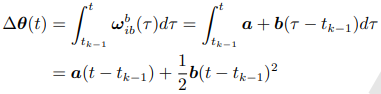
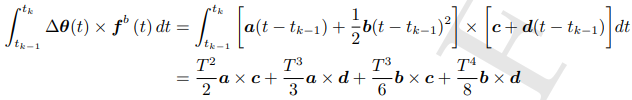
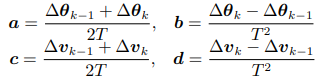
![]()
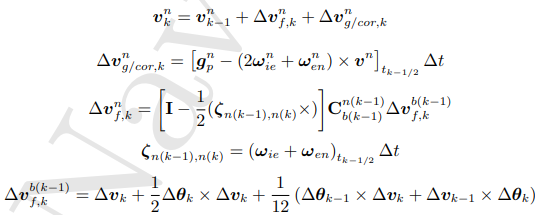
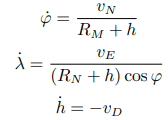

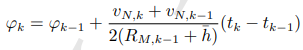
![]()





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 分享一个免费、快速、无限量使用的满血 DeepSeek R1 模型,支持深度思考和联网搜索!
· 基于 Docker 搭建 FRP 内网穿透开源项目(很简单哒)
· ollama系列01:轻松3步本地部署deepseek,普通电脑可用
· 25岁的心里话
· 按钮权限的设计及实现