组合导航原理（三）——使用四元素进行姿态更新

等效旋转矢量

 

 

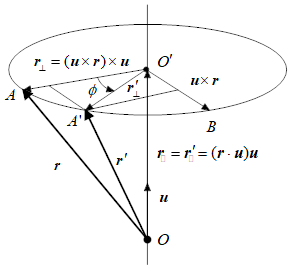
说明 ：

（1）μ是单位向量；

（2）旋转方向，就是使用【右手】握住μ，拇指与μ同向，其余4个手指与旋转方向同向（见角度那个箭头）；

目的：求得r，绕μ旋转Φ角后，得到r'，【r'】为所求；

必要的知识：

（1）点积： r • μ  =  || r || * || μ || * cos<r,μ>，结果是一个【值】。此处 μ是单位向量，r • μ 表示 r 投影在 μ上的长度。

（2）r_// = (r • μ)*μ，表示μ乘以一个长度，是一个【向量】。此处表示：r在μ方向上的分量，。

（3）叉积： μ x r  ，结果是一个【向量】。表示，4个手指与μ方向同向，握向r，结果向量与大拇指方向相同，长度是μ与r围成的四边形面积，因为μ是单位向量，所以面积大小等于r的长度。

 

结果：

（1） r' = r'_// + r'_⊥

（2），r'_{⊥ = O'A'}

 　　  理解：

　　（1）以O'B为Y轴，以O'A为X轴，得到A'的坐标 ( || r'_⊥|| cosΦ ，|| r'_⊥|| sinΦ)，现在|| r'_⊥|| 是未知的，假设已知，后面会消掉。

　　（2）   O‘A  /  || O‘A ||，相当于将 O’A变回单位向量，然后    O‘A  /  || O‘A || * || r'_⊥|| cosΦ  等于 【r'_⊥ 在O‘A  方向上的分量】 

　　（3）又  || O‘A || =  || r'_⊥|| ， 因此： 【r'_⊥ 在O‘A  方向上的分量】 =  O‘A  * cosΦ 

　　（4）同理： 【r'_⊥ 在O‘B  方向上的分量】 =  O‘B  * sinΦ 

　　（5）r'_⊥ = O'A' = 【r'_⊥ 在O‘A  方向上的分量】 + 【r'_⊥ 在O‘B  方向上的分量】 = O‘A  * cosΦ  +  O‘B  * sinΦ 

 

写成矩阵的形式：

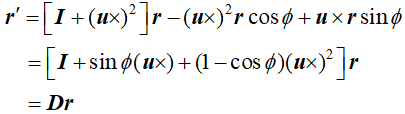
 说明： μ x 可以表示一个μ的【反对称矩阵】，μ x r，可以表示：向量μ “叉积” 向量r、反对称矩阵（μ x）“乘以” 向量r

 

有了上面知识后，那么使用【欧拉角】表示的【旋转矩阵】也可以写成：

Cⁱ_b =  I +sinΦ(μx) + (1-cosΦ)(μx)²

---

四元素的基本知识

 复数：

1.  z  = a + bi， i² = -1

2.  复数相乘，有变换的效果：比如 ：z1 = cosθ + sinθ i， z2 = 1 + 1 i

 z3  = z1* z2 =  ( a * conθ - b* sinθ ) + ( b *conθ + a * sinθ) i

如果展点到【实轴】、【虚轴】上，会发现  z1使得z2旋转了θ度。

这里，可以将z1视为一种变换，z2视为被变换的对象。

 

四元素：

1.  Q = q₀ + q_v = q₀ + q₁i + q₂j + q₃k ； q0是实部；

2.  四元素就是数学家想出来的东西，刚开始看不一定有几何意义。数学家通过加入一些规则，看看运算后有什么有趣结果而已，刚好在姿态更新上可以用得着。

规则：

　　（1）i² = j² = k² = -1

　　（2）i * j  = k  ，j * i  = - k  

　　（3）j * k = i   ，k * j = - i

　　（4）k * i = j ，i * k = - j

助记：

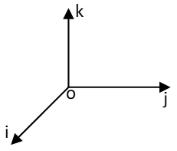
 （使用叉积运算规则，但和叉积不是同一会事，只是助记而已）

3.  四元素之间的运算，资料很丰富。特别需要提及四元素乘法。

 

 四元素乘法：

1. 直接相乘

 

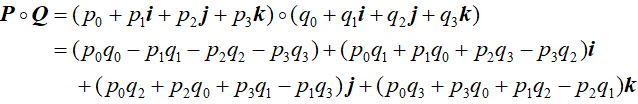
 这个没什么特别，按照普通复数的规则 + 上（1）（2）（3）（4）个规则即可。

2. 以矩阵形式表达

 

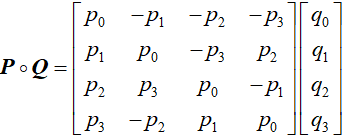
 最后结果，是一个【列向量】，第一个元素是实部。

 

 【四元素】与【方向余弦矩阵】

 

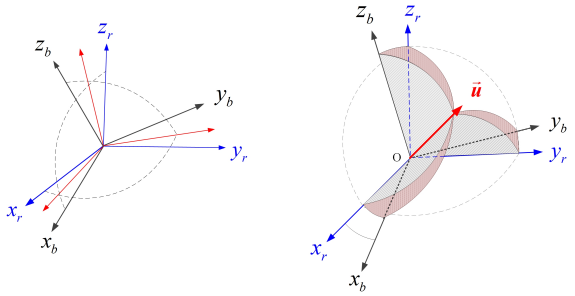
(三个欧拉角旋转，等效一个旋转向量μ + 转角Φ)

 Cⁱ_b =  I +sinΦ(μx) + (1-cosΦ)(μx)²

进行变换：

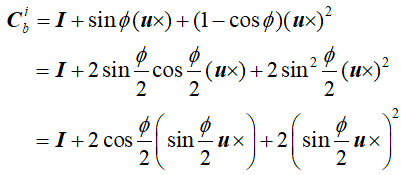
令：

Qⁱ_b = q₀ + q_v

实部：q₀ = cos(Φ/2)

虚部：q_v = μsin(Φ/2)

说明：

1. μ 是 i 系下的旋转向量（轴）。

2. Φ 是等效旋转角。

3. || Qⁱ_b || = 1, μ 是单位向量。又四元素的逆定义：Q^-1 = Q* / || Q|| 。Q*是共轭的意思，虚部符号取反。

4. i系（坐标基）以μ为轴，旋转Φ得到b系（坐标基）

 

 

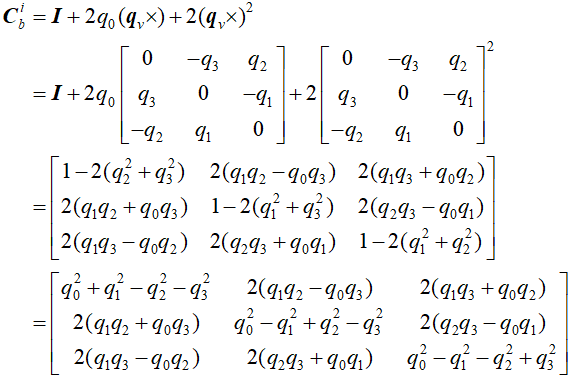
 假设：

（1） 向量r在i系的【坐标投影】r_i = [rⁱ_x,rⁱ_y,rⁱ_z]^T

（2） 向量r在b系的【坐标投影】r_b = [r^b_x,r^b_y,r^b_z]^T

 

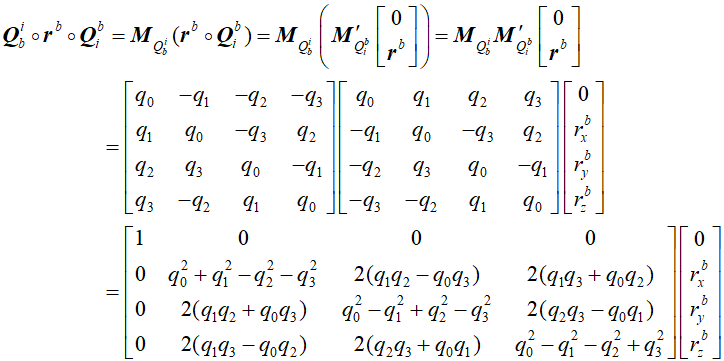
说明：

（1）Q^b_i = (Qⁱ_b)^*，共轭，和普通复数那样，只需要将虚部符号取反。

 （2）Qⁱ_b 是由Cⁱ_b 用到的四元素，是b系变换为i系。而其共轭是由i系转换为b系用到的四元素，比较有意思。

 

【四元素链式法则】 

q^A_B : 表示由B系转到A系用到得四元素。

V^B：向量V在V^B系得投影

 

 

 

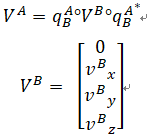
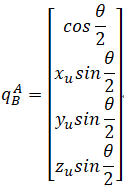
 其中μ在A\B系下的投影坐标是一样的，因为它是不动的。

 

 

 

 

 

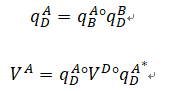
【四元素微分】与【角速度】

根据四元素的链式法则：

q^R_{b(t+Δt)  表示b在 t + Δt时，相参考坐标系转换用到得四元素。}

 _q^Rb(t+Δt) =  q^R_b(t) • q^b(t)_b(t+Δt) 

 Δq^R_b =  q^R_b(t+Δt) - q^R_b(t) = _{q^Rb(t) • q^b(t)b(t+Δt)  -} q^R_b(t)

                             = q^R_b(t)  • (q^b(t)_b(t+Δt) - q₁)

q1 = [1,0,0,0]^T

 假设有旋转向量Δθ，||Δθ|| 是旋转的角度 

必须注意：

（1）||Δθ|| 是一个值，不是向量，||Δθ|| ≠ [ Δθx, Δθy, Δθz]^T

（2）b系在 t 时，绕Δθ向量，旋转||Δθ||角度，变成在t+Δt的b系

 q^b(t)_b(t+Δt) = [ cos(||Δθ||/2),   Δθ / ||Δθ|| *  sin ( ||Δθ|| /2) ]

( Δθ / ||Δθ|| 相当于向量单位化了)

 当  ||Δθ|| 很小时：

（1）cos(||Δθ||/2) = 1

（2）sin ( ||Δθ|| /2) = ||Δθ|| /2

 那么有：

q^b(t)_b(t+Δt)  = [ 1, 1 / 2 Δθ ] (时刻记住Δθ 是旋转向量，不能确定可不可以等同于陀螺输出)

  Δq^R_b  = q^Rb(t)  • (q^b(t)b_(t+Δt) - q₁)  

             = q^Rb(t)  • [ 0 , 1 / 2 Δθ ]

             = 1 / 2  q^Rb(t)  • [ 0 , Δθ ]

 [q^R_b]' = lim [q^R_b(t+Δt) - q^R_b(t) ] / _Δt

           = Δq^R_b    / Δt

           = 1 / 2  q^Rb(t)  • [ 0 , (Δθ)' ]

注意：

（1）时刻记住Δθ 是旋转向量，不是陀螺输出

（2）(Δθ)' 是旋转向量的变化速度，能不能等同于陀螺的角速度，还是不能确定！！

旋转向量的变化速度：

（1）Δθ 是旋转轴，在 t 和 t + Δt 时的 两个 b系，其投影坐标分量都是一样的。

（2）假设 Δθ 在b系的投影坐标 = [ Δθx, Δθy, Δθz ] ^T ( 能不能等同于陀螺的输出，还是不能确定！！)

（3）(Δθ)' = [ (Δθx)', (Δθy)', (Δθz)' ] ^T  =  [ ω^b_Rb,x , ω^b_Rb,y , ω^b_Rb,z]^T

（旋转向量的变化速度，能不能等同于陀螺的角速度，还是不能确定！！）

[q^R_b]'  = 1 / 2  q^Rb(t)  • [ 0 , (Δθ)' ]  = 1 / 2 W q^Rb

 

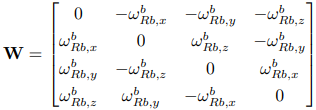
角速度与方向余弦矩阵的关系

四元素与角速度的关系：《捷联惯导算法与组合导航原理》P22有推导过程

 

 

 说明：ωⁱ_ib 在这里也要写成四元素形式，实部为0

ωⁱ_ib = _u^b_ib Φ’ + ( u^b_ib)' sinΦ - uⁱ_ib X( u^b_ib)' (1- cosΦ) 怎么来的？？

（猜测：由方向余弦矩阵和四元素求导，进行对比，找到相似的地方推出来的）

 

 

使用四元素进行姿态更新

 

 

 

 摘抄自书本，可以证实几点：

（1）Δθ 是旋转向量，其||Δθ || 就是由 k -1时刻，到k时刻转过的角度

（2）Δθ =  [ Δθx, Δθy, Δθz ] ^T  = ∫ ω^b_ib(t) dt , 就是陀螺的输出角增量。

（3）[k -1, k] 时间内，旋转向量的分量，就是三轴陀螺的输出角的增量！其长度就是旋转角度，其微分就是陀螺三轴角速度！(有点难想象)

（4）对Δθ求导，得到 (Δθ)' = [ (Δθx)', (Δθy)', (Δθz)' ] ^T  =  [ ω^b_ib,x , ω^b_ib,y , ω^b_ib,z]^T 

（5）最后不要忘记了，将b系测到的坐标，转到i系下， V_i = qⁱ_bV_bqⁱ_b*

 

旋转向量的分量 vs  三轴陀螺的输出角的增量

首先有旋转向量Δθ，||Δθ|| 为旋转角度。

由方向余弦矩阵与【旋转向量】之间的关系：

C = I + sinΦ*μX + （1-cosΦ)(μX)²

 假设μ为旋转向量，是【单位向量】，旋转角度为Φ

 那么当Φ接近0时（必要条件），有：

 C = I +  Φ *μX  

同时，使用 陀螺三轴输出，当作欧拉角进行旋转，又有：

 C^b(t)b(t+Δt) =I +  [ΔΦ,Δθ,Δψ]^T X= I + [ Δθx,Δθy,Δθz]^T X

 C = I +  Φ *μX  = I +  (Φ *μ) X

因此：[ Δθx,Δθy,Δθz]^T X = Φ *μX 

 Φ *μ = Δθ 

因此：

（1）在绕旋转单位向量μ，旋转小角度Φ， [ Δθx,Δθy,Δθz]^T 也是小值的时候

Φ*μ = Δθ。

（2）换句话说，Δθ = [ Δθx,Δθy,Δθz]^T 是旋转向量 μ，模长为Φ = ||Δθ|| 。

（3） Φ = ||Δθ||  ，Φ就是绕μ旋转的角度。

 

因此：

 q^b(t)_b(t+Δt) = [ cos(||Δθ||/2),   Δθ / ||Δθ|| *  sin ( ||Δθ|| /2) ]

 q^b(t)_b(t+Δt) 的Δθ = [ Δθx,Δθy,Δθz]^T就是陀螺的输出