组合导航原理（二）——使用方向余弦进行姿态更新

关于坐标系

导航坐标系n

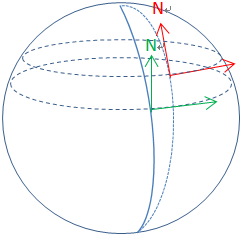
（1） 导航坐标系n相当是跟随载体运动的。（教科书上是：北东地，注意地是向下的）

（教材上，是北，东，地， 这个顺序对应 速度向量的各个元素的位置！ ）

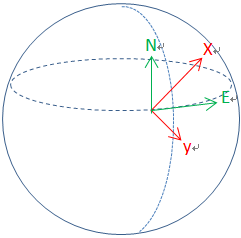
（2）而载体坐标系b，X是前进方向，b系的Z轴和n系的Z轴一般是不平行的，也就是初始时刻，有转换关系Cⁿ_b(0)。

（教材上，是前，右，下，对应X，Y，Z）

 

 

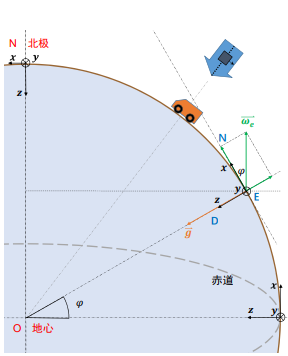
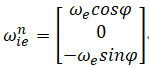
 对于角速度向量的理解：

（1）角速度在R系的投影，就是绕R系各轴旋转的速度。ω^R = [ 绕R系X轴旋转的角速度， 绕R系Y轴旋转的角速度，绕R系Z轴旋转的角速度]

（2）假设e相对于i系的角速度向量 ω^e_ie=   [ 0，0，ω_e]^T,（绕Z轴旋转）

（3） 将ω^e_ie ，放到n系下，并投影到n系下各轴。

 

 

 

 

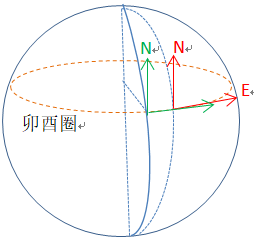
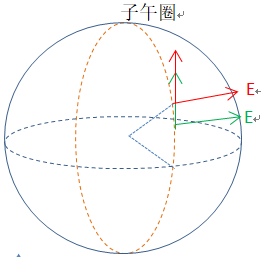
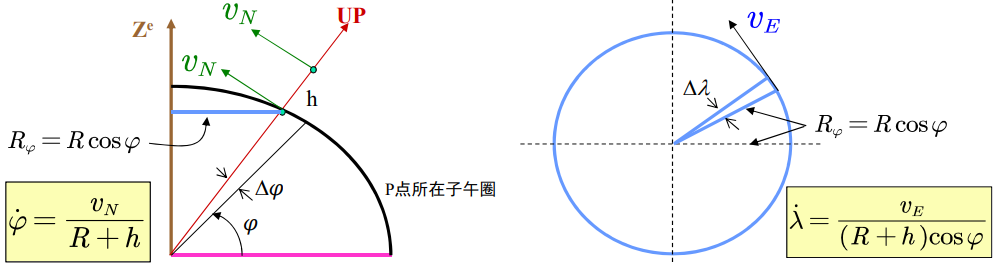
角速度 = 速度 / 运动半径

（1）n系相对于地球系e向东运动，将使得n轴发生旋转。

（2） n系相对于地球系e向北运动，将使得e轴发生旋转，但是方向和右手握的方向相反，所以是负的

 

 

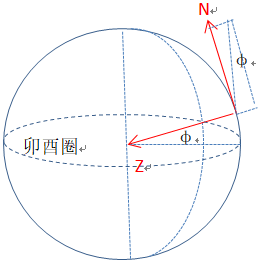
 (3)  平行于地轴的旋转，可以分解成以N轴和Z轴的旋转，利用这个关系得到绕Z轴旋转的角速度

角速度要与半径R运算，才能算出速度 

 

---

 

 

关于旋转矩阵

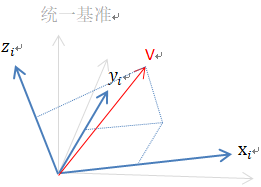 （虚线是i系下的坐标）

 解析：

（1）每个测量设备，只能测出点在它【自身坐标系】下的坐标（向量）。如【红色】的向量在【i系】下的坐标。

（2）如果知道在【统一基准】下【单位向量】 x_i、y_i、z_i，那么就可以通过 【向量V】投影到 x_i、y_i、z_i，就可以得到【V点】在统一基准下的坐标。

（3）如果x_i、y_i、z_i 是单位向量，V点在i系下的坐标是[x_v , y_v , z _v]，在【统一基下的坐标】 = [x_i , y_i , z_i]_3*3 [x_vi , y_vi , z_vi]^T 即可

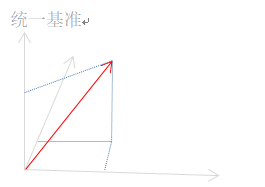（虚线是统一基准系下的坐标）

* [x_i , y_i , z_i]_3*3 是在统一基的列向量， [x_vi , y_vi , z_vi]^T 是参考i系下的坐标。

 坐标之间的转换：

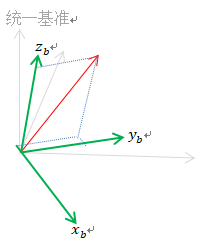（虚线是b系下的坐标）

令：

  [x_i , y_i , z_i]_3*3 是【在统一基】的向量为C_i，

  [x_vi , y_vi , z_vi]^T 是【参考i系】下的坐标为V_i

  [x_b , y_b , z_b]_3*3 是【在统一基】的向量为C_b，

  [x_vb , y_vb , z_vb]^T 是【参考b系】下的坐标为V_b

 【V点】在统一基下的坐标 = C_iV_i= C_bV_b

V_i = C_i ^-1C_bV_b

假设，Ci为单位矩阵，那么相当于i系的各个【坐标基】与【统一坐标基】是重合的。

那么：

V_i =  Cⁱ_bV_b

Cⁱ_b 理解 ：

（1）b系的【坐标轴】，在i系下的向量，通过列向量的形式组织成矩阵。

（2）用于将在【b系下的坐标V_b】，转换到【i系下的坐标】

问题：如何得到Cⁱ_b ？

（1）传感器测量值，只是在【b系下的坐标V_b】，要统一到【i系下的坐标】

（2）如果能测得如下角度：

 

 

 

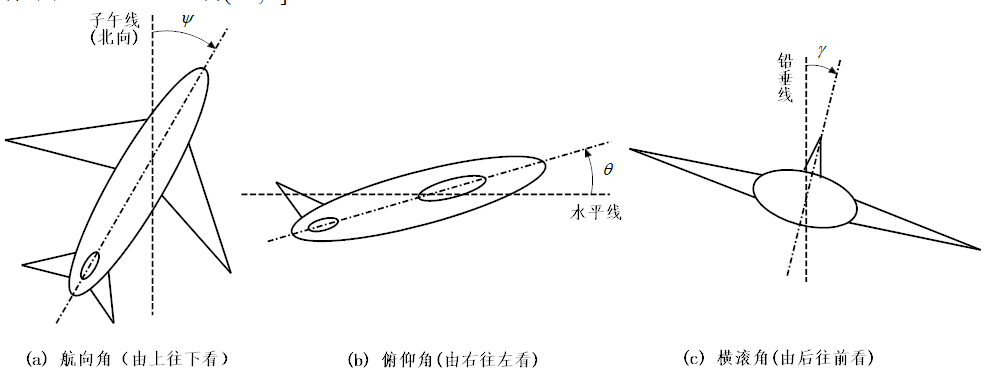
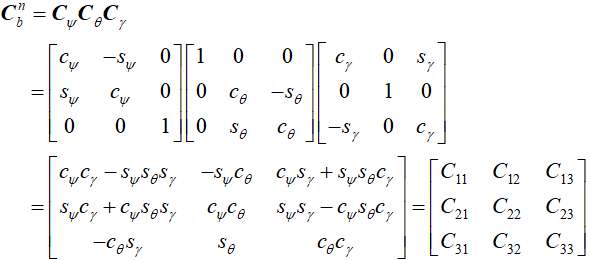
 （注意，公式上的n，在这里应该写为i，图片是其他地方借鉴的）

（3） 有一点很重要的是，Ψ 角是对于i系的x方向（或北向）

（4）问题转化为：如何得到Ψ、θ、γ？

 

---

IMU 角速度测量

 

 说明：

1. IMU只能测出每个时间点的[ω_x,ω_x,ω_z]，它不能直接测出Ψ、θ、γ

2. Ψ、θ、γ 的计算，不是直接对各个时间的[ω_x,ω_y,ω_z] 进行简单的时间积分！！

 

关于角速度

假设：

（1）现在的时间是t_m-1 , 在t_m-1 的瞬间测到角速度[ω_x(m-1),ω_y(m-1),ω_z(m-1)]。

（2）已经得到Cⁱ_b(m-1) （它可以看成是坐标基），假设，现在需要在t_m-1 开始，对Cⁱ_b(m-1) 进行旋转。

那么：

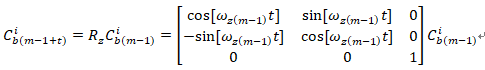
 说明：

（1）t是指，从t_m-1 开始，过去了的时间

那么，在t = 0时刻，对Rz进行求导：

同理：

 

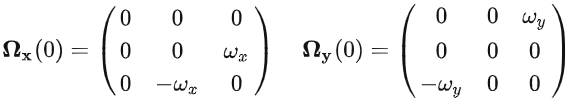
那么，对于

（1）R₁(t) = R_y(t)R_x(t)

（2）R₂(t) = R_x(t)R_y(t)

对【某一瞬间的旋转矩阵求导】，得到的是【角速度矩阵】。（注意要强调某一瞬间，也就是它和Cⁱ_b(m-1) 还没什么关系）

（反过来说，是不是对【角速度矩阵】积分，就能得到【某一瞬间的旋转矩】？？？）

 

 

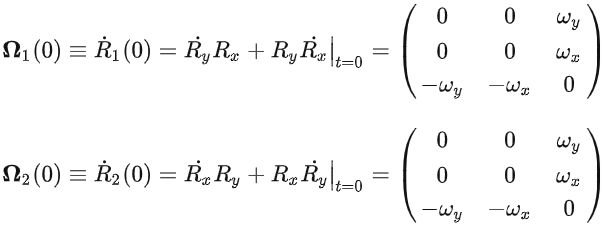
扩展一下：

Ω₁ = Ω₂ = Ω_x + Ω_y

 这告诉我们: 任意绕着xy轴旋转的旋转变换, 其角速度矩阵都可以分解成单独沿着x旋转以及单独沿着y旋转的角速度矩阵的和, 并且这种和是满足交换律的. 进一步的计算可以推广到沿着xyz三个轴的旋转

 

 

 

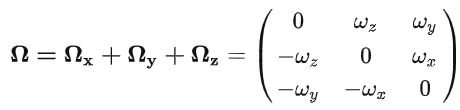
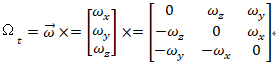
结论：【角速度矩阵】，就是【角速度分量组成的向量】的反对称矩阵。

 

详细推导：

 

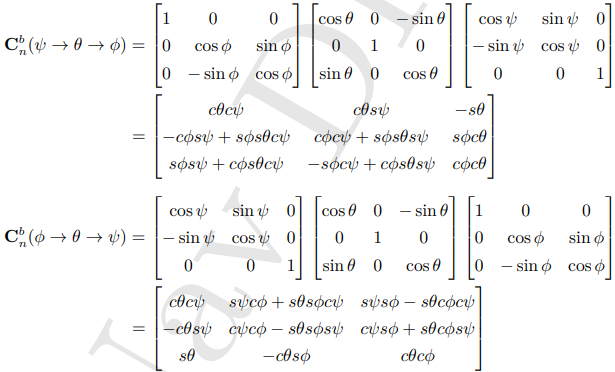
当ψ，Φ，Θ 都足够小的时候，旋转顺序变得不重要

  

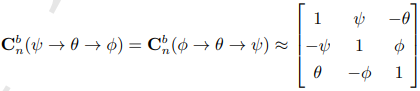
 上面b相当于b(t)，n相当于b(t+Δt)，对C求导相当于[ C^b(t)_b(t+Δt) ]'  ， 对角线求导为0 ， 非对角求导为角速度。 

 下面的东西，可以从这个角度考虑，避免复杂的东西：

（1）Cⁱ_b(t+Δt) = Cⁱ_b(t)*C^b(t)_b(t+Δt)   

（2) [ C^b(t)_b(t+Δt) ]' 求导等于 ω^b_ib x 

（3） [ Cⁱ_b(t+Δt)] ' =  Cⁱ_b(t) * [ C^b(t)_b(t+Δt) ]'  = Cⁱ_b(t) ω^b_ib x 

 

 

 

 关于Cⁱ_b

假设姿态角Ψ、θ、γ ，和均是时间的函数，对式两边同时微分，可得：

 必须注意：

（1）对Ψ、θ、γ 进行微分，并不是得到  [ω_x,ω_x,ω_z] ；

（2）Ψ、θ、γ  是想对于i系的，

（3）而 [ω_x,ω_x,ω_z] 是相当于在时间为t_m-1 的b系的

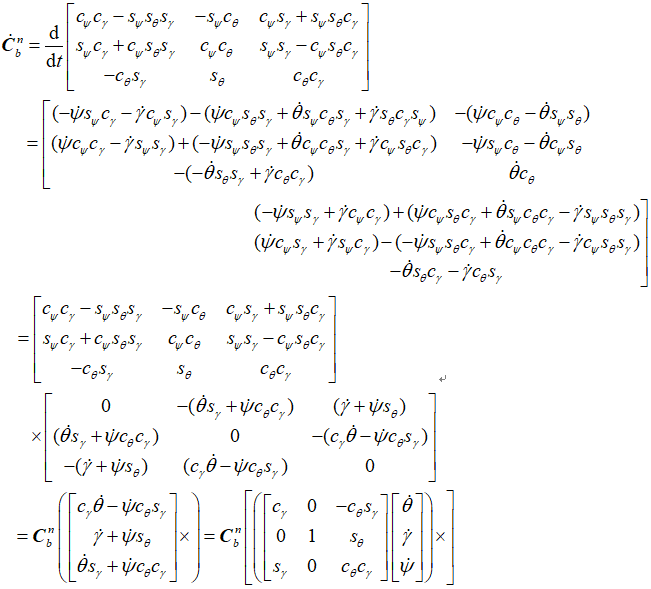
转换一下：

x号是将向量转换为反对称矩阵的意思

 

 

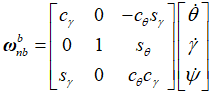
（以上的n，在这里改成i）

【Ψ、θ、γ 的微分】

 

 

 

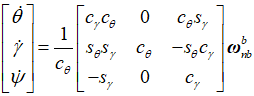
理解：

（1） ω^b_nb ，是b系，相对于i系的【角速度向量】（问题：和【ω_x,ω_x,ω_z】有什么关系？）。

（2）ω^b_nb ，内含 [ θ', Ψ', γ'  ]，ωⁱ_ib  ≠ [ θ', Ψ', γ'  ]^T

（3），好像是在说，【角速度矩阵   [ω^b_nb X] 】，经过Cⁿ_b 进行变换，得到(Cⁿ_b)'

（4）(Cⁿ_b)' ， 就是描述【b系相对于n系】【旋转的速度】。

（5）一般來說，使用   Ω = [ω^b_nb X]

遗留问题：如何将【Ψ'、θ'、γ'】 与【ω_x,ω_x,ω_z】产生联系？

 

 现在假设： 

（1）在时间为t_m-1 的旋转矩阵Cⁱ_b(m-1)  

（2）IMU读取到有t_m-1 的各个轴的旋转速度_， [ω_x(m-1),ω_x(m-1),ω_z(m-1)]

（3）假设ωⁱ_ib 已知（现在暂时没有头绪，除非 [ θ', Ψ', γ'  ]^T 能测出来才能直接算，假设已知）

 

要求：Cⁱ_b(m)  

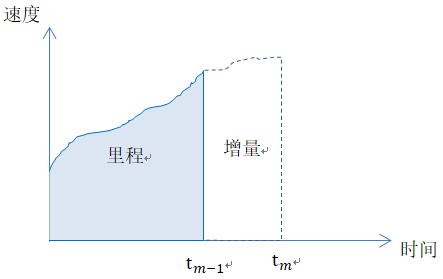
 在《捷联惯导算法与组合导航原理》P14中，有：

Cⁱ_b(m)   = Cⁱ_b(m-1) +  ∫ C'(τ)dτ =   Cⁱ_b(m-1) +  ∫ C(τ) Ω (τ) dτ   ， τ ∈ [0 , t_m - t_m-1] 

(使用Ω(t)代替 [ωⁿ_nb(t) X ])

 

 按照上图，就比较好理解：

1.  Cⁱb(m-1)  理解为里程，相当于b系相对于i系，在t_m-1，已经旋转了多少了；

2.  ∫ C'(τ)dτ 理解为增量；

3. 速度就是C'(t)，因为速度是变的，所以是个函数；

4. Cⁱ_b(m)  理解为在tm 的里程，相当于b系相对于i系，在t_m，已经旋转了多少了；

 

 在《捷联惯导算法与组合导航原理》P15中，介绍了：

1.  Cⁱ_b(m) = Cⁱ_b(m-1) e ^{∫ Ω(τ)dτ} ，τ ∈ [0 , t_m - t_m-1]  （推导过程书上有，还要补充【矩阵积分】、【指数矩阵】）

（注意对比： Cⁱ_b(m)   = Cⁱ_b(m-1) +  ∫ C'(τ)dτ =   Cⁱ_b(m-1) +  ∫ C(τ) Ω (τ) dτ ）

2. 【可交换性条件】， 是Cⁱ_b(m-1) e ^{∫ Ω(τ)dτ}   Cⁱb(m-1) +  ∫ C(τ) Ω (τ) dτ ）的【必要条件】。（书上有证明）

   （1）必须要补充一点，使用进行v_i = Cⁱ_b v_b 旋转计算，等价于v_b绕某一固定【向量μ】，旋转α度。

　（2）可以由Cⁱ_b 计算出【向量μ】。事实上μ 是 Cⁱ_b 【特征值】为1的【特征向量】。（查看【罗德里格斯公式】）

3. 【可交换性条件】，直白点说，就是在[0 , t_m - t_m-1]  时间内，Cⁱ_b等效使用【罗德里格斯公式】进行旋转的向量μ，必须是固定的。换句话说，[0 , t_m - t_m-1]  时间内，采集频率必须很高，高到旋转向量μ来不及发生变化。

 

重点来了！！！！！！！（希望有人告诉我是不是这样？？）

Ω(τ) =  [ωⁱ_ib(t) X ] = [ ω_x(t),ω_x(t),ω_z(t) ]^T X

ω(t) = [ ω_x(t),ω_x(t),ω_z(t) ]^T

（书上竟然没有说！！，是直接写出来的，为啥会这样？）

也就是：

 

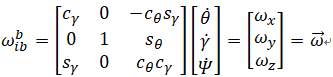
 苦苦要求的ωⁱ_ib 竟然就是IMU能够直接输出的三轴角速度【ω_x,ω_x,ω_z】

 

再求 Cⁱ_b(m) = Cⁱ_b(m-1) e ^{∫ Ω(τ)dτ}

令：T =  t_m - t_m-1， 那么 τ ∈ [0 , T]

《捷联惯导算法与组合导航原理》P16中，有公式：

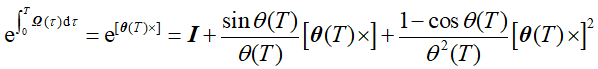
ω(τ)  = 【ω_x(τ),ω_x(τ),ω_z(τ)】

Cⁱ_b(m) = Cⁱ_b(m-1) e^[θ(T)X]

说明：

（1）sinθ(T) = sin(||θ(T) ||) ，θ(T) 是向量

（2）θ(T) 可以看成来，是[0 , T]期间，三轴旋转的【角度增量】，注意不要和【Ψ、θ、γ】的增量混淆

 注意：【ω_x,ω_x,ω_z】 不是传感器直接输出的吗？那怎么得到在[0, T]之间的角度函数ω(τ)  = 【ω_x(τ),ω_x(τ),ω_z(τ)】？？？？

 

 

猜想：（希望有人告诉我是不是这样？？）

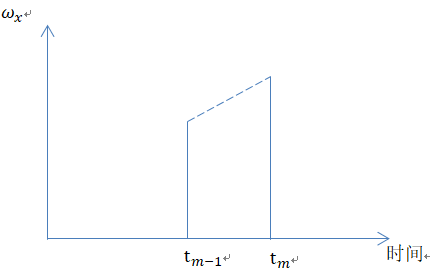
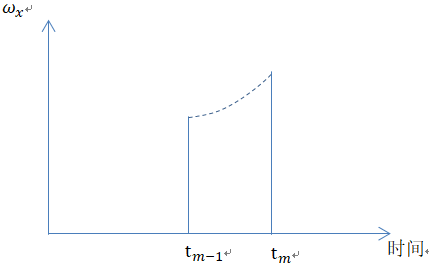
 单独对ω_x 进行建模，例如上面，可以假设多项式：

ω_x(τ) =  at + b

ω_x(τ) =  at² + bt + c

 

最简单的姿态更新算法流程：（希望有人告诉我是不是这样？？）

 

后续：

 

关于【指数矩阵e^A】的误区：

千万不要将e^A 想象为

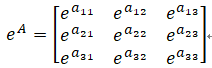
而是：

 

 

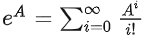
所以，求解e^A =  I + A + A2/2! + A3/3!，根据A的特性决定到哪一项？？？

 

---

 

接上

误区一：IMU测量的是【角增量】，上一时点，到下一时间点的【角度增量】。

*  IMU还会测量 【比力】，f_b = a - g

 

 猜测：

 

 （1）ω(t) 的函数是不好确定的，那么用ω积分来计算角积分，会带来损失；

 （2）可以想象成汽车， 每个时刻的里程（角度增量）更加容易得到，也更加准确。就像直接得到了图上积分的区间面积一样。

 

误区二：关于e^A

 如果A 是反对称矩阵，A = VX，那么有准确的解析解：

 

 

需要补充的知识

1. 各种参考坐标系：https://blog.csdn.net/absll/article/details/124764404

（1）i系：原点在地心，x轴指向春分点，Z轴与自转轴重合。一般认为是绝对不动的坐标系。

（2）n系：导航坐标系。实际上惯性导航最终要将结果解算到此坐标系下。

（3）b系：载体坐标系。以IMU为重心，IMU的轴为XYZ轴的系。

（4）e系：地心地物坐标系。x轴指中央子午线与赤道交点，随着地球一起转动。

 

2. 角速度定义

假定有符号：ω^p_Rb  

坐标系b，相对于【参考系R】的角速度，在坐标系P下的投影。

容易得到：ω^p_Rb   =  - ω^p_bR

 

3. 重点：角度叠加公式

   ωⁿ_ie + ωⁿ_en = ωⁿ_in 

ωⁿ_en ： 导航坐标系，相对于地心地物坐标系的角速度。（由载体的运动速度有关）

 ωⁿ_ie ：地心地物坐标系，相对于绝对静止的i系得角度。（由地球自转角速度、纬度有关）

 ω^b_ib ：这是IMU理论上的角速度，这就是说，IMU的角速度是绝对的。（猜测！）

 

 

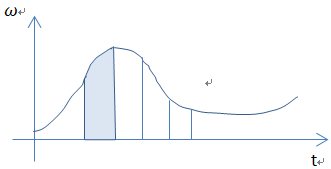
4. 转换矩阵的说明

（1）符号说明

Cⁿ_b：由b系转换到n系，通常也是求姿态的结果。 [Ψ(t),θ(t),γ(t)]^T 就是b系相对于n系旋转的欧拉角。

Cⁿ_b(m)  ：Cⁿ_b 是随时间变化的，所以，加入了时间m。意思是：在t = m时，由b系转换到n系。

C^b(t)_{b(t + Δt)} ：b系相对于自身也是会发生变化的，意思是：由 T = t + Δt时的b系，转换到T = t 时的b系。

例子：IMU输出了在 T = t + Δt 的角度增量 [ Δθ_x,Δθ_y,Δθ_z  ] ^T , 可以认为，b系在T = t + Δt时，相对于b系在T = t 时，旋转了[ Δθ_x,Δθ_y,Δθ_z  ] ^T 

直接可以用【小角度欧拉角旋转矩阵】，近似计算出C^b(t)_{b(t + Δt)}

 

（2）链式计算  C^d_a = C^d_bC^b_a

这个很好理解，由a转到b，再b由转到d，等于a转到d。

利用这个办法：

Cⁿ_b(k)  = C^n(k)_n(k-1) C^n(k-1)_b(k-1) C^b(k-1)_b(k) 

C^n(k-1)_b(k-1) 可以写成Cⁿ_b(k-1) 

解析：

（1） C^b(k-1)_b(k) 上面有了。对应的角速度是： ω^b_ib  直接是IMU得出（其实IMU测得是Δθ = ∫ω^b_ib(t)dt）！！！！不是ω^b_nb 

（下面对Cⁿ_b 微分，用的是ω^b_nb  有区别）

（2）Cⁿ_b(k-1) 是上一次更新好的值，已有。

（3）C^n(k)_n(k-1) 导航系也是在运动的，地球动它也动，因为IMU的角度是相对于i系，所以一切相对于i系会动的东西，都要考虑进去。

 要记得：ωⁿ_in   =    ωⁿ_ie + ωⁿ_en ， 就是计算C^n(k)_n(k-1) 要用到的角速度。

 

5. 姿态叠加无意义

 [Ψ(t),θ(t),γ(t)]^T
不要试图对某时的欧拉角进行加减： [Ψ(t),θ(t),γ(t)]^T +  [Ψ(t+Δt),θ(t+Δt),γ(t+Δt)]^T 

这样做是无意义的 [Ψ(t+Δt),θ(t+Δt),γ(t+Δt)]^T  只能通过变换，变为 [Ψ(t),θ(t),γ(t)]^T

 

6. 小角度欧拉角旋转矩阵（非常重要）

 

 

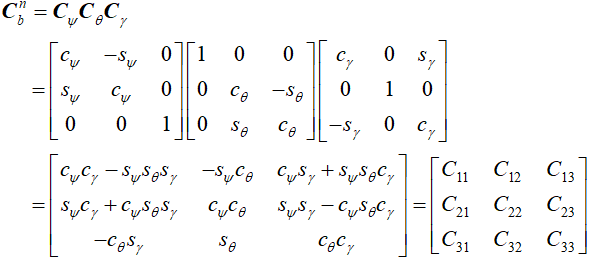
  [Ψ(t),θ(t),γ(t)]^T 都是小角度时：

（1） [Ψ(t),θ(t),γ(t)]^T 都是小角度，只会发生在b系在t_k时，相对于b系在t_k-1时，的欧拉角，也就是C^b(k-1)_b(k) 用到的。在Cⁿ_b ，b相对于n的欧拉角不是小角度 ！！

（2）sinΨ ≈ Ψ  ,  联想一下在sin函数在0处的斜率 k =1

（2）sinΨsinθ = Ψθ ≈ 0 ; 两个小等于0

（3）cosΨ ≈ 1

那么：

 

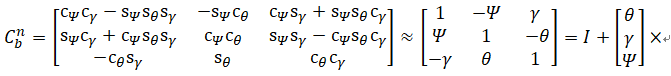
换句话说：

 

 

 

 

 要注意的地方：

（1）要根据欧拉角旋转的顺序，定义Δθ向量的顺序。

（2）Δθ = [Δθx ,Δθy,Δθz] ，就是IMU在t = k时刻输出的角度增量。

 

7. 另一种方式求(C^R_b(t))'， 方向余弦矩阵微分

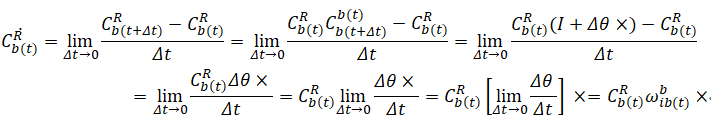
（这里有误，应该是ω^b_Rb (τ)，要b系相对于R系的角速度）

 

8. 

Ω (t) =  ω^b_nb(t) x

注意：是b相对于n的角速度，因为下面要求的是Cⁿ_b

但是：如果IMU测得角速度（ω^b_ib）又是绝对的，所以又有转换关系  

 

接上：

Cⁿ_b(t+Δt)   = Cⁿ_b(t) +  ∫ C'(τ)dτ =   Cⁿ_b(t) +  ∫ C(τ) Ω (τ) dτ

加上【可交换条件（ t ~ t +Δt 期间定轴旋转）】，得到：

Cⁿ_b(t+Δt) = Cⁿ_b(t) e^[ΔθX]

那么，可以得知：

C^b(t)_b(t+Δt)  =  e^[ΔθX] （ 就好像是李代数，旋转矩阵C对应李代数Δθ）

对比：

C^b(t)_b(t+Δt)  ≈  I + ΔθX

更加准确

 

遗留的问题：

要求载体系b相对于导航系n

Cⁿ_b(t+Δt) = Cⁿ_b(t) e^{∫Ω (τ) dτ}=Cⁿ_b(t)C^b(t)_b(t+Δt)

Ω (τ) = ω^b_nb(t)，b系相对于n系的角速度。

但是载体系b相对于惯性系i

Cⁱ_b(t+Δt) = Cⁱ_b(t) e^{∫Ω (τ) dτ}= Cⁱ_b(t)C^b(t)_b(t+Δt)

Ω (τ) = ω^b_ib(t)，b系相对于i系的角速度。

问：IMU输出的是 Δθ = ∫ω^b_ib(t)dτ ，不是Δθ = ∫ω^b_nb(t)dτ ，应该怎么办？

 （1）C^i(t)_b(t) =  C^i(t)_n(t)C^n(t)b(t)

 （2）Cⁱ_b(t+Δt) = C^i(t)_b(t)C^b(t)_b(t+Δt)  , 这里用的是Δθ = ∫ω^b_ib(t)dτ 

 （3）（1）代入（2）得到：

            Cⁱ_b(t+Δt) = C^i(t)_n(t)C^n(t)b(t)C^b(t)_b(t+Δt)

 （4）作业两边，乘以 Cn(t+Δt) i(t+Δt) ，得到：

         Cn(t+Δt) i(t+Δt)Cib(t+Δt) = Cn(t+Δt) i(t+Δt) Ci(t)n(t)Cn(t)b(t)Cb(t)b(t+Δt)

左边化简：

 Cn(t+Δt) b(t+Δt) =  Cn b(t+Δt)  = Cn(t+Δt) i(t+Δt) Ci(t)n(t)Cn(t)b(t)Cb(t)b(t+Δt)

思考一个问题：

 Ci(t+Δt) n(t+Δt) 与Ci(t) n(t+Δt) 有无区别？

应该是没有区别的，因为i是不动的，所以i在t和t+Δt 状态一样， 那么： Ci(t+Δt) n(t+Δt) =  Ci(t) n(t+Δt) ，从而   Cn(t+Δt) i(t+Δt) = Cn(t+Δt) i(t)

因此：

 Cn b(t+Δt)  = Cn(t+Δt) i(t) Ci(t)n(t)Cn(t)b(t)Cb(t)b(t+Δt)

　　           = Cn(t+Δt) n(t) Cn(t)b(t)Cb(t)b(t+Δt)   , 这里用的是Δθ = ∫ωbib(t)dτ , 是IMU的输出

而：

Cn(t+Δt) n(t) = [ Cn(t)n(t+Δt)  ]T

根据方向余弦矩阵微分的结论：

C^n(t)_n(t+Δt) =   e^{∫Ω (τ) dτ}  ， Ω (τ) =  ∫ωⁱ_indτ 

ωⁱ_in 是 导航系相对于惯性系的角速度，根据【角速度叠加】法则：

   ωⁿ_ie + ωⁿ_en = ωⁿ_in 

ωⁿ_en ： 导航坐标系，相对于【地心地物坐标系】的角速度。（由载体的运动速度有关，可以计算）

 ωⁿ_ie ：【地心地物坐标系】，相对于绝对静止的i系得角度。（由地球自转角速度、纬度有关，可以计算）