组合导航原理（一）

 

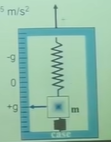
 IMU垂直方向输出（当以上为正方向时）：

（1）静止时： 约等于-g

（2）运动时：a - g

（3）实际加速度 a = 输出 + g

 

一维惯性导航

 

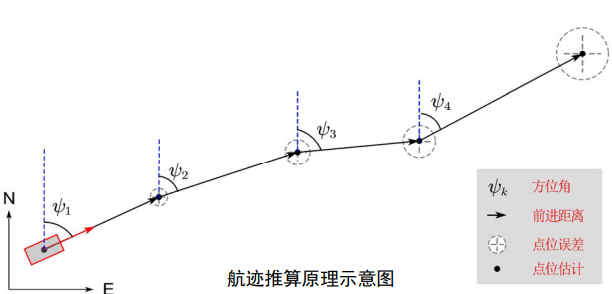
 理解：

（1） 假定 【前进方向】与【传感器方向】是一致的。

（2）一开始，测定【前进方向】的【方位角（Azimuth）】

（3）假设某时刻 t 角度增量 > 0 , t + 1时刻角度增量为0 ， 那么 t 到 t+1时刻的位移可以直接算出。

 

使用加速度求行走距离

 

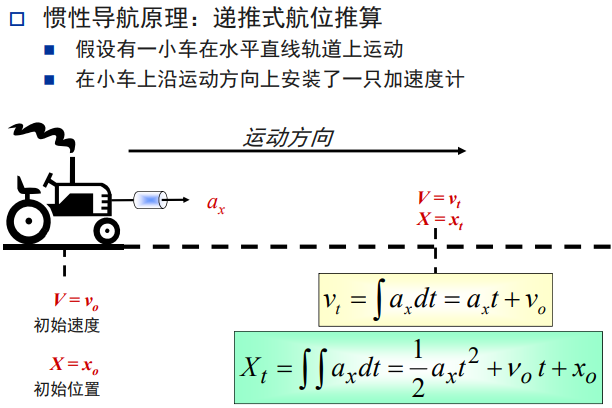
平台式系统

 

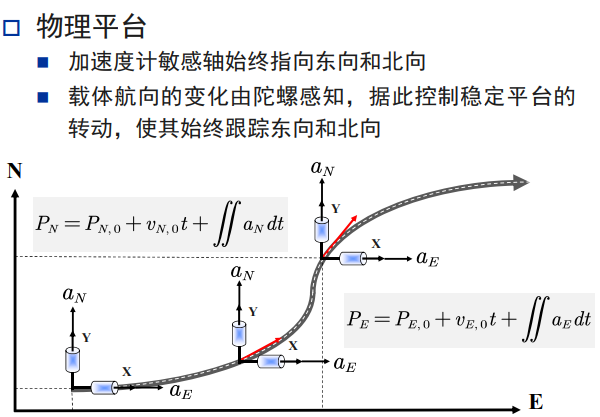
 理解：

（1）【前进方向】与【传感器方向】不一致，传感器正向一直是指向【参考系】正方向的。

（或者说，前进方向与传感器方向，关系是一直在变的）

（2）蓝色【小圆柱】应该代表的是一小段时间

 

 捷联式

 

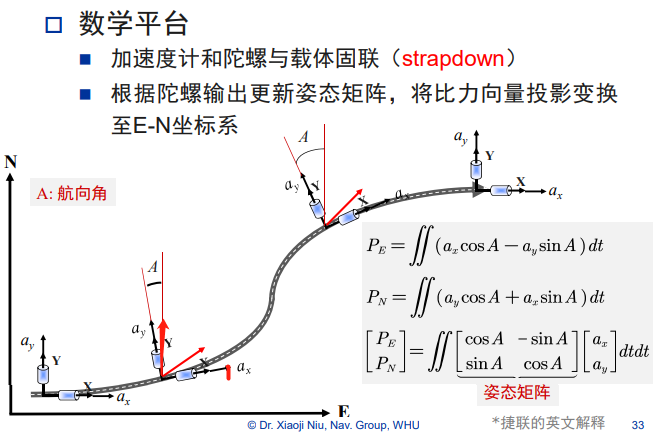
 理解：

（1）前进方向与传感器方向（或载体主轴与传感器主轴），关系是固定的。

（2）传感器始终是输出他主轴方向的加速度

（3）加速度是矢量，因此可以使用【向量投影】、【向量相加】的方式叠加。

（4）【姿态矩阵】，相当于引入了【旋转】 

（5）A不是直接由陀螺给出的，陀螺只能给出【角速度】，猜测：

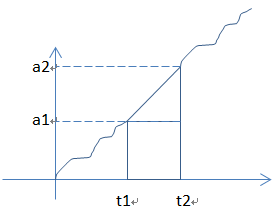
 在t1测得角度a1

 在t2测得角度a2

a1在 [ t - 1, t ]怎样变到a2的，不知道，假设在[ t - 1, t ]期间，【角速度函数】为 f(t)

假设 f(t) = kt + b ，也就是角速度是均匀变换化的，那么 k = Δa /  Δt , b = a₁ -  k * t₁

  f(t) = k t + b

角度增量 = ∫ f(t) dt，积分范围是 [ t1, t2] 

∫ f(t) dt =  1 / 2 * k * t₂² + b * t₂ - 1 / 2 * k * t₁² - b * t₁

           =  1 / 2  *  k  * （ t₂² - t₁² ） +  b * (t₂ - t₁) 

           =   1 / 2  * Δa  * （ t₂  + t₁  ）+  (a₁ -  k * t₁)Δt

           =   1 / 2  * Δa  * （ t₂  + t₁  ）+ a₁ Δt - Δa * t1

           =  1 / 2  * Δa * Δt  + a₁ Δt

(中间部分放大)

A_t = A_t-1 + 角度增量