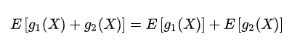概率论（四）——数学期望\方差\协方差

数学期望

设离散随机变量X的概率质量函数为：

如果：

则称：

为随机变量X的数学期望（expected value，或，expectation），简称期望或均值（mean），也有很多文档会用μX来表示（如果不强调随机变量的话，也可以直接用μ来表示）：

若级数不收敛，则称X的数学期望不存在。

 

如果p(x)是连续的，有：

∫ p(x) dx = 1

那么：

E(x) =  ∫  x p(x) dx

---

 

数学期望例1

假设要开设彩票投注，一次投注应该如何定价合理？

1000元，概率0.5%，P(1000) = 0.05%

100元，概率5%，P(100) = 0.5%

5元，概率10%，P(5) = 10%

1000 * 0.5% + 100 * 5% + 5 * 10% = 1.5 

那么，每次投注  > 1.5元才有得挣

 

数学期望例2

 

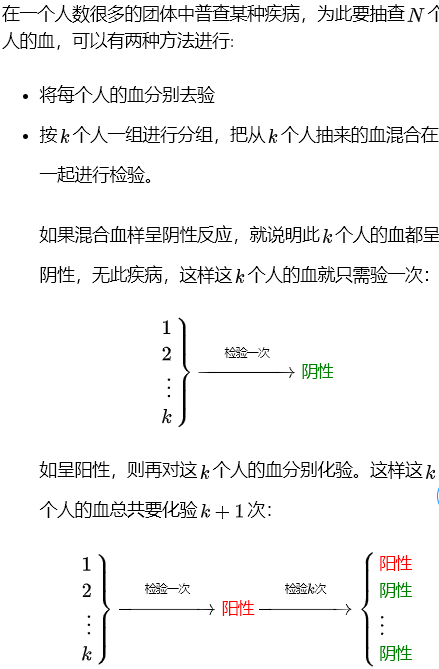
假设 X是检测的次数，发病率为p

那么：

P(X = 1) =  (1 - p)^k ,  全部都没有发病，就检测一次

P(X = k + 1 ) =  1 - P(X = 1)  = 1 -  (1 - p)^k , 只要有一个发病，就检测1 + k次

【检测总次数】的数学期望：

E(X) = 1 * (1 - p)^k   + ( k + 1) * [ 1 -  (1 - p)^k  ] 

如果已知发病率p，那么可以计算 【每人平均检测次数】的期望 = 1 / k * E(X)  

【每人平均检测次数】的期望    = 1 / k  * (1 - p)^k   + ( 1 + 1 / k) * [ 1 -  (1 - p)^k  ]  

                                                   =  1 -   (1 - p)^k  + 1 /  k

最好能得到 k  = argmin(  1 -   (1 - p)^k  + 1 /  k  )

或者将目标设定为：【每人平均检测次数】的期望   < 1，那么就是已经优化了问题了

 

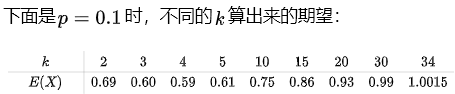
 可以得到 当p = 0.1时，4人一组可以使得【每人平均检测次数】的期望 最小。

 

 

数学期望例3

已知某国的平均身高是 E(X) =  μ = 1.718米，求身高为171.8米的概率

已知：

E(X) = ∑ p(xi) * xi

所以：

p(171.8) * 171.8 < E(x)

p(171.8) * 171.8 <  1.718

p(171.8) < 1% 

 

数学期望例4

p( x ≥ 171.8) = ？

p( x ≥ 171.8) = p( 171.8) + p( 172.8) + p( 173.8) +....

171.8 * p( 171.8) + 172.8 * p( 172.8) + 173.8 * p( 173.8)... ≤ E(X)

 下面也是成立的：

171.8 * p( 171.8) + 171.8 * p( 172.8) + 171.8 * p( 173.8)... ≤ E(X)

171.8 * ( p( 171.8) + p( 172.8) + p( 173.8) +....)  ≤ E(X)

也就是： 

171.8 * p( x ≥ 171.8)  ≤ E(X)

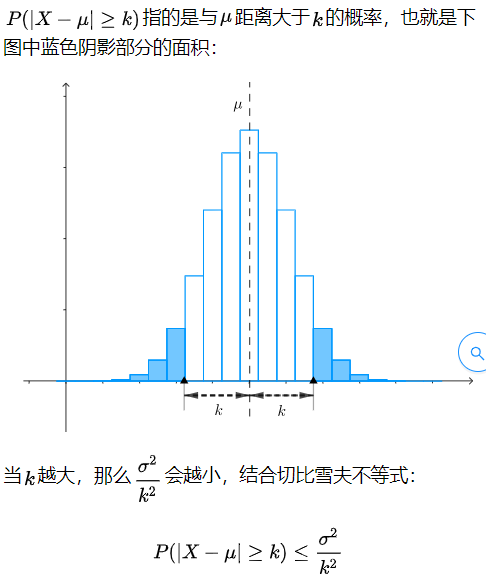
马尔可夫不等式

 p( x ≥ a) ≤ E(X) / a

 

根据官方数据，中国人均收入为51350元（假设收入皆为正数），那么年入超过百万的人会超过10%吗？

p(x≥1000000) ≤ 51350 / 1000000 < 10%

 

---

数学期望图解

（一）秤的右侧

 

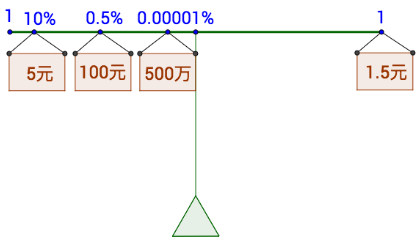
 (备注：右边是算出的期望，X等于秤砣，概率等于杆长，X* P等于力矩)

 （二）重心

 

 

 

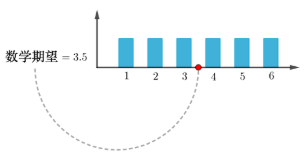
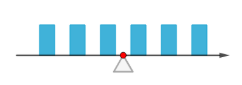
 （备注：所有随机的X都会围绕在数学期望附近，例如这个图，X出现在100，即离开数学期望足够远的概率为0）

 

 

 

---

 

数学期望性质 

 复合：

理解为：p(g(x_i))的概率和p(x_i)是一样的

 

线性组合：

 

常数 ：

E(c)  = c

 

 备注：g1(x_i) + g2(x_i)  的概率为p(x_i)

E(g1(X) + g2(X)) = ∑ pi * (g1(x_i) + g2(x_i)) = ∑ pi *  g1(x_i)  + ∑ pi * g2(x_i) 

 问题：可不可以认为，g1(x_i) 、g2(x_i)的概率，分别都是p(x_i)？？

 

---

 方差标准差

引子：

身高1米7，河水平均深度1米3，看起来是安全的，但是下去遇到水中的深坑就淹死了。所以我们还需要知道河水的深度范围，比如说1米3±0.2米，那么就是安全的，最深就是1米5，最浅是1米1

 

如何量化【稳定性】？

 

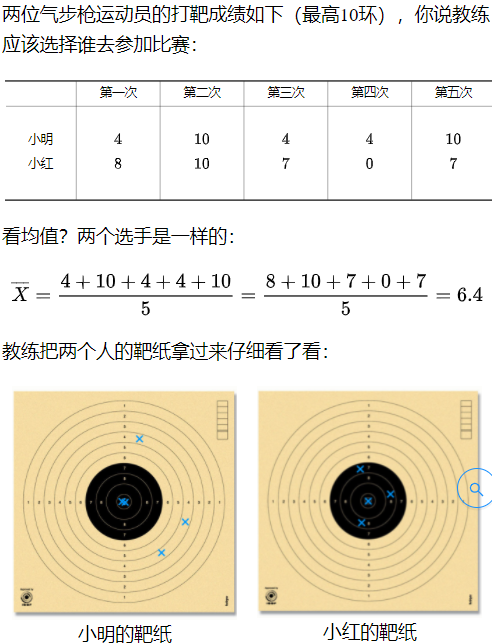
量化的结果，应该是： 小红的稳定性 > 小明的稳定性

【稳定性】等于【集中性】，那么问题转化为：如何量化【集中性】？

一维下：

 

 

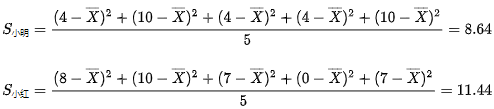
（注意，是：【距离平方和均值】 ， 不是【距离均值】）

高维度下：

 s  =  ∑ 欧氏距离 / n ， 注意：欧氏距离不是距离平方，有区别。

 

方差定义

参考协方差矩阵：几种特殊的矩阵和用途（一） - 耀礼士多德 - 博客园 (cnblogs.com)

 

方差可以写作：

 

如果p(x_i)  =1  / n，那么写成矩阵形式：  σ² = 1 / n * [ X - μ]^T[ X - μ]_n*1

 

 展开式：

 

思考：

认为 P((Xi - μ)²) = P(Xi) = 1 / n

*根据【数学期望复合】原理，E(g(X)) = ∑g(Xi) p(Xi)，认为 p (g(Xi)) = p(Xi) 

 

方差的性质

E( ( X - μ)^T( X - μ ) ) = E(X^TX - X^Tu - μ^TX + μ^Tμ ) 

　　　　　　　　    = E(X^TX - 2u^TX + μ^Tμ ) 

　　　　　　　　    = E(X^TX) -  2E(u^TX) + E(μ^Tμ ) 

　　　　　　　　    = E(X^TX) -  2E(u^TX) +  μ^Tμ  

　　　　　　           = E(X^TX) -  2E(μ^T)E(X) +  μ^Tμ 

　　　　　　　　    = E(X^TX) -  2μ^Tμ+  μ^Tμ 

　　　　　　　　    = E(X^TX) -  μ^Tμ 

　　　　　　　　    = E(x²) -  μ²

 

 

E(c) = 0

 

误差传播

Var(aX + b) = a²Var(X) + b 

 

标准差

 

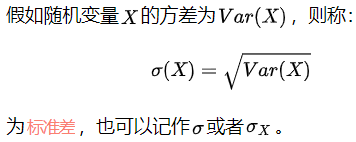
 根据标准差的定义：X分布在 μ = E(X) 的σ范围内的概率最大，最集中。