概率论（三）——概率分布函数

二项分布

P( true ) = p

P( false ) = 1 - P( true )  = 1 - p 

X = true

X ~ b( n , p)

例子：

n个独立测试中，有k个为true的概率：

X = true

记作：X ~ b( n , p)

P =   C^k_n * p^k( 1 - p)^{n - k}

例1：

 

假设有n个独立测试，其中x次为true的概率： P(x) = C^x_n * p^x( 1 - p)^{n - x}

E(X) =    ∑ x* P(有x次为true)   = np

Var(X) = np*( 1 - p)

 

 

泊松分布

 

 

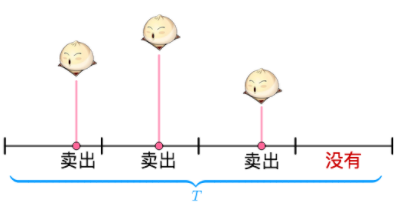
 假设每个时间段，卖出馒头的概率是p，卖不出是 1 - p

 那么，在T时间段内，将T分成4份，卖出三个馒头的概率为：

P =   C³₄ * p³( 1 - p)^{4 - 3}

 若卖出馒头的时间分布不均，那么会：

 

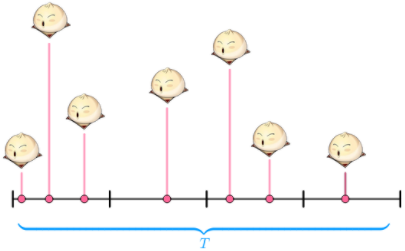
 那么，可以再将时间T分成更多份

 

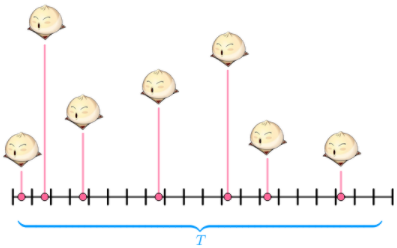
 P =   C⁷₂₀ * p⁷( 1 - p)^{20 - 7}

若将T分割成n份，那么【在T时间内，发生K次结果为true的概率】，已知【事件为true的概率为P】

P =  lim   C^k_n * p^k( 1 - p)^{n - k} , n -> ∞

 

 

 

 

累积分布函数

 

 F(a)  =  P( X ≤ a )  

 P( X > a )  = 1 -  F(a) 

 P(  a1 ≤ X ≤ a2 )  =   F(a2)  -   F(a1)