概率论（二）——条件概率

在你面前站着一个陌生人，看他的样子要对你开口说话

那他开口会不会是中文？我们完全不知道。按照古典派，说中文的概率和说任何一门语言的概率是一样的，比如英文：

但如果知道他是中国人，那说中文的概率会大大增加；

而如果是英国人，概率就会大大减少;

 即：

P( 中文 | 中国人)  >  P(英文 | 英国人 )

条件概率就是计算样本空间缩小时的概率

 条件概率，就是将样本空间Ω变为样本空间

 

 将样本空间C去掉（相当于只考虑B），那么Ω = B

 

 

 

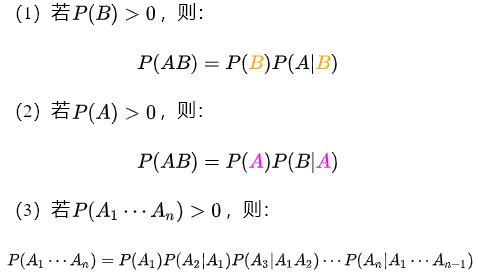
贝叶斯定理

 

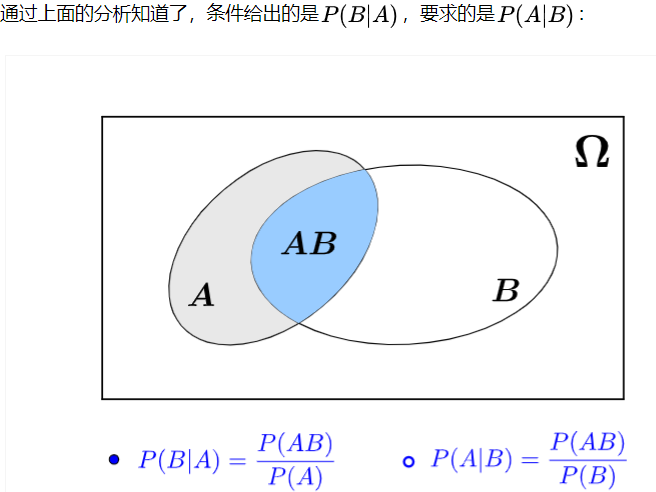
 用集合的角度看待：

P(AB) =  既是A也是B的个数 / Ω的个数

P(B) =   B的个数 / Ω的个数

P( B | A) = 既是A也是B的个数 / A 的个数

理解： B | A  相当于将AB的样本空间，从Ω缩小至A

P(AB) =  P( B | A) P(A)  = P(A | B) P(B)

理解：A发生的概率 * A发生后B发生的概率 = AB同事发生的概率

变换一下：

 

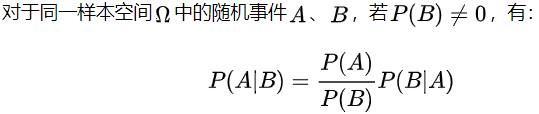
例子1：

【已知检测的正确率为90%】，分析这句话：

 P(检测有病 | 有病) =  90%  

 P(检测没病 | 有病) =  10%  

 P(检测没病 | 无病) =  90%  

 P(检测有病 | 无病) =  10%  

可以定义：

A = “有病”

B = “检测有病”

假设，人群中【已知有病】的概率为2%，这里又叫【先验】，就是事先经过大量统计得到的概率，那么：

1. P(A) = 2%

2. P(!A) = 98%

P(B) =  P(检测有病 | 有病)  * P(有病)   +  P(检测有病 | 无病)  * P(无病)

        = 90% * 2% + 10% * 98%

P( B | A ) =  P(检测有病 | 有病) =  90%

可以得到：

P(A | B) = P( 有病 | 检测有病)  = P(B|A) / P(B) * P(A)

 

 

例子2：

 

//

 

 例3：

 

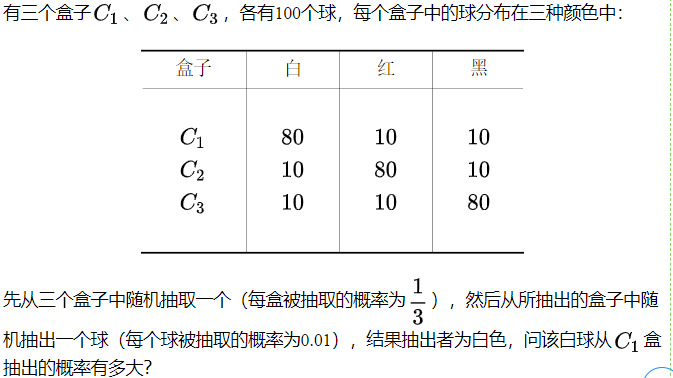
令：

B = “抽出白球”

Ai = "从Ci中抽出球"

P( 因 | 果)  = P(A1 | B)

由贝叶斯公式：

P(A1B) = P(A1)P(B |A1) = P(B)P(A1 | B) 

P(A1 | B)  = P(B |A1) / P(B) * P(A1)

P(A1) = 1 / 3， 样本空间是Ω 

P(B | A1) = 80 / 100， 样本空间是A1，所以是100

*必须注意到样本空间

P(B) = P(BA1)+ P(BA2)  +P(BA3)

        =  P(B|A1) * P(A1) + P(B|A2) * P(A2) +P(B|A3) * P(A3)

        =  80 / 100 * 1 / 3 + 10 /100 * 1 / 3 + 10 /100 * 1 / 3

       

或者可以将P(B) 的样本空间理解为Ω

那么: P(B) =  (80 + 10 + 10) /  300

 

---

 

贝叶斯修正

A  = “下雨”

B1 = “有乌云现象”

P(A|B1) = P(B1|A) / P(B1)  * P(A)

B2 = "闷热现象"

P(    A | 。。。 ) =  P( B2 |  A) /  P(B2)  *   P(B1|A) / P(B1)  * P(A)

反正就是得到， “出现了各种现象下，下雨的概率”

---

 独立事件

P(AB) = P(A) * P(B)

P(B) = P( B | A )，也就是A发生不发送，B的概率都一样，A条件对B没作用