概率论（一）——集合

集合&概率

概率论，使用集合的方式表示：

 

 

 

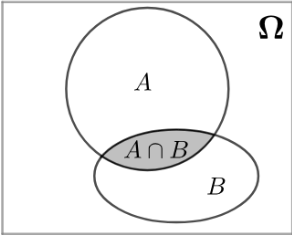
 理解：

P(A) + P(B) ，相当于把  A∩B加了两次，要减去一次

 

乘法原理&枚举

 

 

 

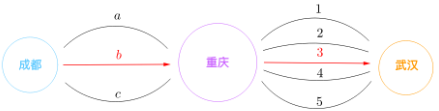
 理解：

不需要将所有结果都列出来，只要 P(b) = 1 / 3， P(3) = 1 / 5， P( b ∩ 3) = 1 / 3 * 1 / 5  = 1 / 15 

P( b & 3) = 1 / 3 * 1 / 5  = 1 / 15 

 

加法原理&枚举

 

 

 

 

 理解：

不需要将所有结果都列出来，只要 P(1) = 1 / 6， P(3) = 1 / 6， P(5) = 1 / 6 ，

  P( 1 ∪ 3 ∪ 5 ) = 1 / 6 + 1 / 6 +1 / 6 = 1 / 2

  P( 1 | 3 | 5 ) = 1 / 6 + 1 / 6 +1 / 6 = 1 / 2

 

有顺序的n选r

_ , _  ,  _ 

样本空间个数为 P^r_n  =  n * ( n -1) * .....( n - r + 1)

理解：

有序是指，（第一次选A，第二次选B，第三次选C）  的概率
 

无顺序的n选r

与上面有区别的是：

（第一次选A，第二次选B，第三次选C）

（第一次选C，第二次选B，第三次选A）

以上两种只能算是一种

C^r_n = P^r_n / r ! = n! /  (r!  * (n - r )!)

样本空间：C⁴₉    = 9! / (4! * (9 - 4)!) = 126 种

B = 从6件合计品种取出两件 = C²₆ = 6! / (2! * (6 - 2)!) =  15

C = 从3件不合计品种取出两件 = C²₃  = 6! / (2! * (6 - 2)!) = 3

P(A) = C²₆ *  C²₃ / C⁴₉ = 15 * 3 / 126

 

长度&概率

 

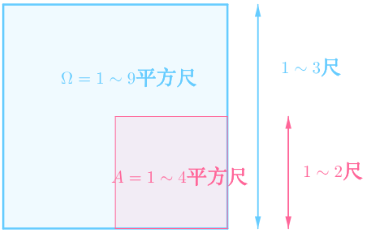
 Ω是整个样本空间

 

 

 对应的面积：