卡尔曼滤波（八）——其他角度理解
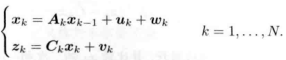
xνk 为第k时刻的【先验】
x^k 为第k时刻的【后验】
uk理解为【常数项】、wk~N(0,R)理解为模【型误差项】、vk~N(0,Q)，理解为【观测值误差项】
p(wk) = N(0,R)， p(vk) = N(0,Q)
【先验】：就是【状态的猜测】，根据之前的状态，猜测当前的状态。
【后验】：暂时理解为【状态的优化结果】，根据先验、观测值优化得到的结果。
使用贝叶斯公式：非线性优化 - 耀礼士多德 - 博客园 (cnblogs.com)
理解：
（ 1 ）这是一个模型方程，模型的用法：xνk = Akx^k-1 + uk，等价于：第k时刻的先验 =Ak* 第k-1时刻的后验
( 2 ) 那么，第k时刻的【先验 P( xνk ) 】服从的高斯分布，是均值为 ：Akx^k-1 + uk ，【先验协方差】矩阵为：AkP^k-1AkT + R
（ 3 ）系统的输出，就是 【后验状态x^k 】、以及【后验P^k协方差】，为第 k + 1 次估计服务。
那么，问题就是：
1. 如何得到第 k时刻的【后验状态x^k 】
2. 如何得到第 k时候的【后验P^k协方差】
如果使用贝叶斯公式：
P( x^k | zk) = P( zk | xvk) * P(xvk) / P( zk) ， 因为zk 是已经发生的事，认为P( zk) = 1，那么：
P( x^k | zk) = P( zk | xk) * P(xvk)，即：后验概率 = 似然 * 先验
*【似然】，怎样的xk ， 使得观测值为zk 的概率最大
结合高斯分布：
N(后验状态 , 后验协方差) = N(x^k , P^k) = N(Cxk, Q ) * N(xvk , Pvk)
