几种特殊矩阵和用途（四）
旋转的表示：
1. 使用坐标基的形式。 几种特殊矩阵和用途（二） - 耀礼士多德 - 博客园 (cnblogs.com)
2. 使用欧拉角。连接同上。
3. 使用旋转向量。几种特殊矩阵和用途（三） - 耀礼士多德 - 博客园 (cnblogs.com)
4. 使用四元素。
5. 李群与李代数。李群与李代数 - 耀礼士多德 - 博客园 (cnblogs.com)
6. 使用【罗德里格斯公式】。R = cosθ * I + (1 - cosθ) nnT + sinθ * n^，Rn = n，n是R特征值为1的特征向量。
7. 使用【罗德里格斯矩阵】。
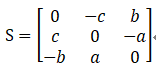
ST = -S
( I - S )T = ( I + S)
RT = [ ( I + S )( I - S )-1 ] T =[ ( I - S )-1 ]T ( I + S )T
= [ ( I - S )T ]-1( I + S )T
= ( I + S) -1 ( I + S )T
= ( I + S) -1 ( I - S )
R-1 = [( I + S )( I - S )-1 ] -1
= ( I - S ) ( I + S )-1
( I + S )-1 = 1 / 2 * ( I + S ) -1 * 2I
= 1 / 2 *[ ( I + S ) -1 * ( I + S + I - S)]
= 1 / 2 *[ ( I + S ) -1 *( I + S) + ( I + S ) -1 (I - S)]
= 1 / 2 ( I + R-1)
RT - R-1 = 1 / 2 * [ ( I + R-1)( I - S ) - ( I - S )( I + R-1) ]
= 1 / 2 * ( S R-1 - R-1S )
（向量叉积 A x B = A^B， A = [a,b,c]T , A^是向量A对应的反对称矩阵）
已知坐标转换模型：
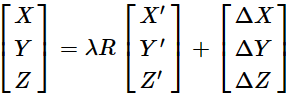
目标：计算λ、R、[ΔX,ΔY,ΔZ]
先计算λ
将两个坐标系的公共点的坐标均化算为以重心为原点的重心化坐标
重心：[ ∑X / n，∑Y / n ，∑Z / n]T
X和X‘分别减去各自的重心，就是重心化坐标了。
重心化后，两个坐标系的坐标，分别记为：
、
两个重心化坐标处理后，有如下关系：
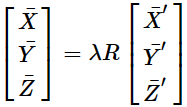
（认为无论如何缩放、旋转、平移，重心依然是重合的）
如果由其中一个点，得到λ
（这个很好理解，重心化后，相当于一个同心球，坐标离原点的距离就是【范数】，范数的比例就是比例因子）
λ = || [X',Y',Z']T || / || [X,Y,Z]T ||
最小均方估计
X = KX'
求 K = argmin ∑1 / 2 * ( KX' - X)² = ∑( 1/2K²X'² - KXX‘ + 1/2X²)
令：δ (∑(1/2 K²X'² - KXX‘ + 1/2X²)) / δK =∑ (K X'² - XX‘ ) = ∑K X'² - ∑XX‘ = 0
K = ∑XX‘ / ∑X'²
