计算相机运动

对极几何——单目相机

假设，能在相片1、相片2中，都找到同名点P1、P2、...Pn

 

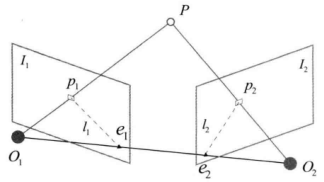
说明：

1. 相机中心为O₁，O₂

2. 相机从I₁到I₂之间，有旋转R，位移t

3. P点在照片I₁，I₂的上的点，为p₁，p₂，并且有很多这样的P点。(p₁对应p₂ 通过图像算法的特征匹配来获得一个匹配索引，I₁的[n,m]对应I₂的[i, j ])

4. O₁、O₂、P形成的面，叫【极平面】

5. O₁、O₂ 与相片平面的交点e₁,e₂，叫【极点】

6. O₁、O₂ 的连线，叫【基线】

7. O₁O₂P面，与I₁，I₂面的交线，叫【极线】

根据 ： 相机模型 - 耀礼士多德 - 博客园 (cnblogs.com)

 

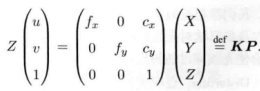
说明：

1. P在 I₁ 坐标系下坐标为[X,Y,Z]^T，有： Zp₁ = KP ， 此处 p₁ = [u₁,v₁,1]。

 

 

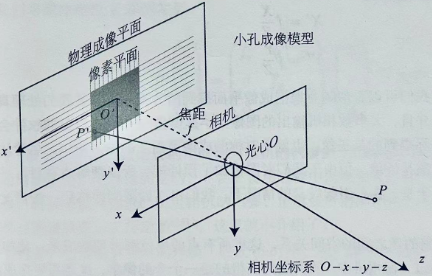
2. P在I₂坐标系下的坐标为 RP + t （相机旋转了R，位移了t），有： Z₂p₂ = K(RP + t ) ， 此处 p₂ = [u₂,v₂,1]

（注意，这只是一个模型，已有XYZ都是无法得知的，因为距离Z得不到）

 

可以令：

1.  p₁ = Z₁ [u₁, v₁, 1 ]， p₂ =Z₂ [u₂  , v₂  , 1  ]， 先令：p₁ = KP，p₂ = K(RP + t ) 

2.  x₁ = K^-1p₁ ( x₁ 实际上不就是P ？) ，x₂ = K^-1p₂， 那么有：x₂ = Rx₁ + t， x₂是P在I₂坐标系下的坐标，因为p₂ = Kx₂

3. x₁、x₂、与向量t做叉积，  相当于  t^x₂ =  t^Rx₁ + 0

4.  上面式子，左右两边乘以 x₂^T ，    x₂^Tt^x₂ =  x₂^Tt^Rx₁

5. t^x₂就是一个向量，垂直于t 与 x₂形成的面，那么 x₂^Tt^x₂ = 0

7. x₂^Tt^Rx₁ = 0

8. 代入p₁ , p₂得到     (K^-1p₂)^Tt^R K^-1p₁  = 0 ， 即：p₂^T (K^-1)^Tt^R K^-1p₁  = 0， (K^-1)^T写成  K^-T ，那么：p₂^T K^-Tt^R K^-1p₁  = 0

 注意：这里p₁ = Z₁ [u₁, v₁, 1 ]， p₂ =Z₂ [u₂  , v₂  , 1  ]，可以将Z₁ ，Z₂ 消去，得到下面式子，而下面式子 p₁ =   [u₁, v₁, 1 ]， p₂ =   [u₂, v₂, 1 ]

对极约束——p₂^T K^-Tt^R K^-1p₁  = 0 

令：

1. 【本质矩阵】 E = t^R 

2. 【基础矩阵】F = K^-TE K^-1

那么，有：

1. x₁ = K^-1p₁

2. x₂ = K^-1p₂

3. x₂^TEx₁ = 0

 

---

 

假设  A是本质矩阵，A = t^R = TR（t是相机位移，R是相机旋转）

A = U_3*3 ∑_3*3 V_3*3^T.........(1)

由奇异值分解的性质，有：

UU^T= I, VV^T = I

AA^T = TR(TR)^T = TRR^TT^T = TT^T .......(2), 因为 RR^T = I

 AA^T = (U∑V^T)(U∑V^T)^T = U∑V^TV∑U^T = U∑²U^T......(3) 因为 VV^T = I

U是AA^T 的特征向量，∑²是AA^T的特性值。意思是，得到∑²就能得到A的特征值

 由（2）得：

 

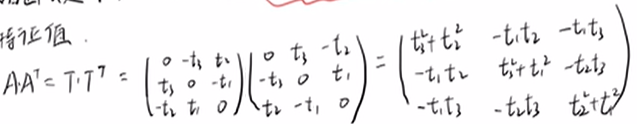
 解： | λE - TT^T |  = λ( k - λ)² = 0 ， k = t₁² +  t₂² +  t₃² = k

 那么∑²对角为 λ1 = 0， λ₂ = k，λ₃ = k

 那么 【本质矩阵A】的特征值为0，√k ， √k （两个相等，一个为0）

---

 

矩阵知识补充：

1. P是正交矩阵，那么 PP^T= PP^-1=  I，从而P^T = P^-1

2.  已知A是对称矩阵，那么一定有 A = Q∑Q^T SVD分解 - 耀礼士多德 - 博客园 (cnblogs.com)

那么，如果有正交矩阵P，P^TAP  = D，D是A的特征值对角矩阵。 证明：

P^TAP  = D 等价于 P^-1AP = D， 因为P^T = P^-1

 P^-1AP = D 等价于 A = PDP^-1

A = PDP^-1等价于A = PDP^T， 形式和A = Q∑Q^T 一致，那么D = ∑

---

 

观测     x₂^TEx₁ = 0 ，E乘以任意常数，等式依然成立，那么：

1. x₁ = K^-1p₁ = Z₁K^-1[u₁,v₁,1]^T   

2. x₂ = K^-1p₂ = Z₂K^-1 [u₂,v₂,1] ^T 

先抛开   Z_1， Z₂，或者令Z₁,Z₂融入到E中，那么：

1. E ' =  Z₁ Z₂ E ，x₁ =K^-1[u₁,v₁,1]^T  , x₂ =K^-1[u₂,v₂,1]^T   (E本身各个元素都未知的)

2 . 对于 x₁ ，它可以变为Z归一化的坐标令  x₁  =  k₁x₁ ， x₁ = [u₁,v₁,1 ] ，注意：这个u1,v1 和  p1 = [u₁,v₁,1]的含义不同，他是归一化算出来的，p1直接是照片中的位置

3 . 对于 x₂ ，它可以变为Z归一化的坐标令  x₂  =  k₂x₂， x2 = [u2,v2,1 ] 

4. 那么 E '' =k₁ k₂ Z₁ Z₂ E  , E相当于乘以一个常数而已，k₁ k₂ Z₁ Z₂ 相当于一个尺度常数。 

 那么，有x₂^TE''x₁ = 0，左右两边乘以 1 / k₁ k₂ Z₁ Z₂，可以得到：

 

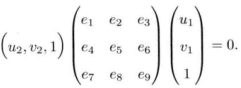
解出E‘’，就能解出E

变换一下：

 

 

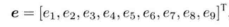
 *因为方程是   Ax = 0的形式，所以不能用最小二乘法了，因为A^TAx = A^T0 无什么意义，只能用8个点解8个未知数

A_8*9E_9*1 = 0

如果A的各个行线性无关，那么e = 0 , 或e是一条直线，垂直于行空间。

那么e = ce₁ , e₁为其中一个特解，可以让其为单位向量

 一般来说，特征点大于8个，可以使用最小二乘解：

 

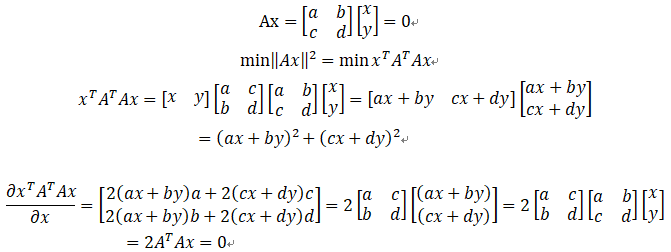
 解 ： A^TAE = 0

---

 

已知A的奇异值为σ，σ，0

那么：A^TA =    V∑U^TU∑V^T = V∑²V^T

 ∑² =  diag(σ,σ,0)

那么，有：

P^TA^TA P = P^TV∑²V^TP ， 若 P = V，那么：P^TA^TA P =∑² = Λ 

令：

B = P^TAP  ， 将B = (b₁,b₂,b₃) ， b₁,b₂,b₃ 都是 3 *1 的

B^TB = (P^TAP)^T(P^TAP) = P^TA^TPP^TAP = P^TA^TAP = Λ = diag(σ,σ, 0)

展开：

 

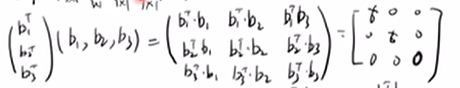
 b₁^Tb₁ = b₂^Tb₂ = σ

 b₁^Tb₂ = b₁^Tb₃ = b₂^Tb₃ = 0

取正交矩阵 Q₁ = (c₁,c₂,c₃) , 令：

c1 = b₁ / √σ

c2 = b₂ / √σ

c₃^Tc₃ = 1

c₃^Tb₁ = 0

c₃^Tb₂ = 0

（那 c3 = c₁ x c₂ ，并单位化）

Q₂：

 那么，Q₁^TP^TAPQ₂ = Q₁^TBQ₂ ，定义为D

 

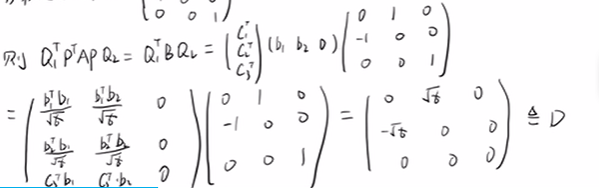
Q₁^TP^TAPQ₂ = D

A =  (Q₁^TP^T)^TD(PQ₂)^T = PQ₁DQ₂^TP^T 

P与Q₁为正交矩阵，那么Q₁P正交矩阵，（PQ₁)^T PQ₁= I。（ Q₁P(Q₁P)^T = I）

A =   PQ₁D I Q₂^TP^T  = PQ₁D  (PQ₁)^T PQ₁ Q₂^TP^T

令：

T = PQ₁D   (PQ₁)^T

R = PQ₁ Q₂^TP^T，R为正交矩阵。（正交矩阵乘以正交矩阵，结果为正交矩阵）

A = TR

又 D^T = -D ， T^T = [  PQ₁D   (PQ₁)^T ] ^T =  PQ₁D^T(PQ₁)^T   =  - PQ₁D(PQ₁)^T = -T，T为反对称矩阵

 

---

 

求出E后，对E进行SVD分解

E = U∑V^T

主要是为了得到 U和V，而∑可以是：

diag(σ₁+σ₂ / 2，σ₁ + σ₂ / 2，0)，或直接（1，1，0）

根据上面，有

本质矩阵A =   PQ₁D I Q₂^TP^T = TR = t^R

其中：

T = PQ₁D   (PQ₁)^T

R = PQ₁ Q₂^TP^T

由有罗德里格斯公式：R = cosθ·I + ( 1 - cosθ)nn^T + sinθ·n^

 令：

θ  = Π / 2

n =  [0,0,1]

那么R_z(Π / 2)，表示绕Z轴旋转Π / 2 ，为：

 

 

R_z^T(Π / 2)  = Q₂............................(1)

R_z( - Π / 2) =  Q₂ = R_z^T(Π / 2)

R_z^T( - Π / 2) =  Q₂^T............................(2)

又：

A = U∑V^T= PQ₁D Q₂^TP^T = TR = t^R

直接可以得到：

U = PQ₁， 都是正交

∑ = D Q₂^T =  - diag(√σ,√σ,0)， √σ 刚好为A的特征值

V = P

t^  =  T = PQ₁D   (PQ₁)^T  = U D U^T ,  又 ∑ = D Q₂^T ， D = ∑Q₂

那么，t^ = U ∑Q₂ U = U ∑R_z( - Π / 2)  U ，  或 t = U ∑R_z(  Π / 2)  U

R = PQ₁ Q₂^TP^T = U R_z^T( - Π / 2) V^T ， 或 R =  U R_z^T(  Π / 2) V^T

 

 

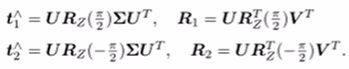
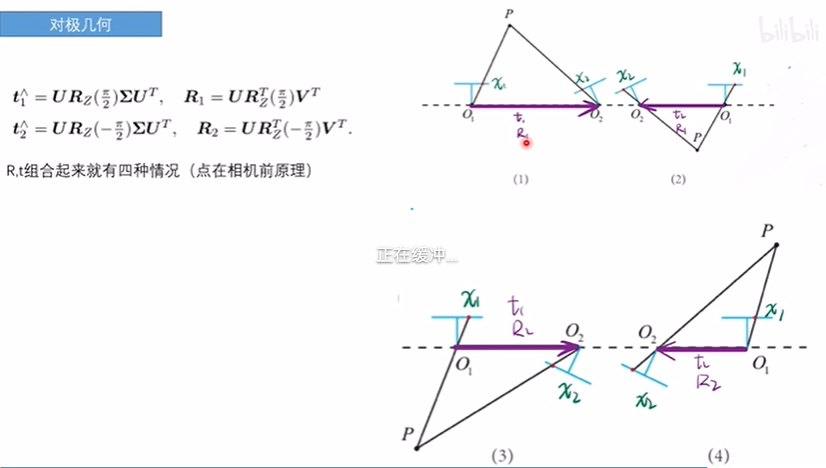
 t1，t2是互为相反的

如何判断是哪种解？

因为已经有 z₂p₂ = K(RP+t)， 4个解都代一下，得到z₂大于0的那一种，就是物体在相机前的那种，就是真正的解。

 

---

 

对于任意的旋转矩阵R，和三维向量v，有：

(Rv)^ = Rv^R^T

证明：

∀u∈R³，Rv x Ru = R(v x u)，v x u 是一个向量，垂直于 v和u。先叉积再旋转，等价于先旋转再叉积。

等价于(Rv) ^ Ru = Rv^u

等价于(Rv) ^ R = Rv^ 

等价于(Rv) ^  = Rv^ R^T （RR^T = I）

 

---

单应矩阵

如果两张照片匹配好的特征点，在现实中位于同一平面上时，有：

n^TP+ d = 0，

- n^TP / d  = 1

n是平面法向量，P是点的坐标。

又：

 z₂p₂ = K(RP + t)

　　  = K(RP + t * 1)

         = K(RP + t * - n^TP / d)

         =  K(R + t * - n^T / d) P

又：

z₁p₁ = KP

P = K^-1(z₁p₁) 

 z₂p₂ = K(R + t * - n^T / d) K^-1(z₁p₁) 

令：

H_3*3  = K(R  - t *  n^T / d) K^-1 ， 为【单应矩阵】

 z₂p₂ = H(z₁p₁)  

令：

H = z₁/z₂ * H， 相对于将深度信息融到H阵中 

 

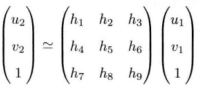
u₂ = h₁ * u₁ + h₂ * v₁ + h₃

v₂ = h₄ * u₁ + h₅ * v₁ + h₆

1 =   h₇ * u₁ + h₈ * v₁ + h₉

 等价于：

 

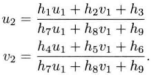
令 h₉ =1

 

 

 

 

---

 

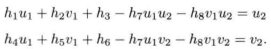
直接线性变换（DLT）——求深度

设某个点在I₁中的相机空间坐标为 P = [X,Y,Z,1] ^T

投影到照片上的特征点x1 = [u₁,v₁,1] ^T (归一化坐标)

他们有如下关系：

 

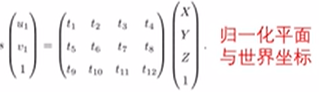
 （这个3 x 4的矩阵，包含了旋转、平移、内参的信息，但是揉到一起了）

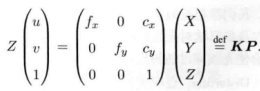
（以前是这个模型的）

消去最后一行（注意消去的方法，消去但不减少元素个数）

 令：

 

 

 

 

---

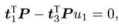
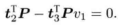
 P3P——得到点在相机坐标系下的3D坐标

 

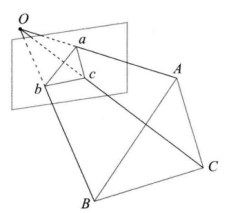
 已知ABC三点，在【世界坐标系】下的坐标

（ABC的面，不一定平行于abc面）

 根据余弦定理：

 

 

 

 

 

 

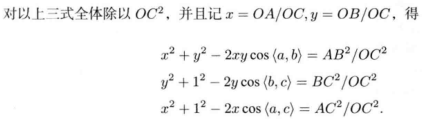
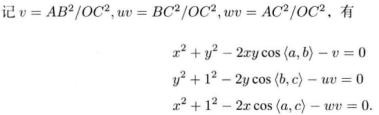
 a,b,c在图像上的位置是已知的，焦距f也是已知的，因此：

cos<a,b>、cos<b,c>、cos<a,c>

都是已知的

u = BC² / AB² 、w = AC² / AB²

u、w也可以根据A、B、C三点得到

 

---

 

PNP

先求相机位姿，再求空间点位置

假设三维空间点P（[X,Y,Z]^T）

根据相机位姿的变化R、t，有

 （a就是P，a‘就是第二个位置下，P的相机坐标系坐标P’）

又知道相机内参K，对于每张照片，都有：

 

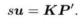
 展开：

 

 

 

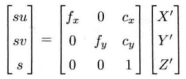
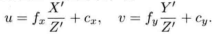
 两个公式结合，得到在第二张照片下，P点在照片上的位置：

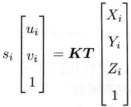（s_i就等于Z）

 

 

 

 

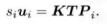
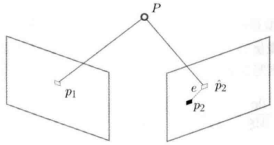
相机位姿，可以先有一个估计值T₀，（假设旋转了多少，位移了多少），可以推测在照片I₂上，位置是p₂’

实际上，拍下的照片的位姿是p₂

 有T₀，转换为对应李代数Φ

T = exp(ξ^)

目标求得：

 （u_i也就是照片上的p₂）

对上式 e = 1 / 2 ∑(u_i  - 1 / s_i * KTP_i)²求导，并使其为0，实际上是对ξ求导：

但是对ξ求导比较复杂，改为使用扰动模型：T = ΔTT₀ = exp(δξ^)exp(ξ^)，δξ是ΔT对应的李代数

又  ：

1. P'  = TP_i =ΔTT₀ P_i ( 在第二张照片上)

2. 

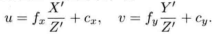
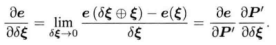
所以：

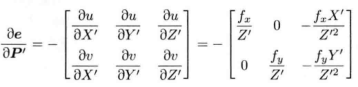..............................(1) 

接下来求：∂P‘ / ∂δξ

 

 P' = RP + t

............................................(2)

 

 (1)(2)相乘：

 

---

 

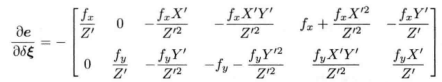
ICP

参考：用SVD求解ICP问题的完整证明 - 知乎 (zhihu.com)

相机在两个位置，分别测得相机坐标系下的点：

1. P = {p₁, p₂,...p_n}

2. P' = {p'₁, p'₂,...p'_n}

∀i，p = Rp' + t，p'是前一帧

误差模型：

e = p  - (Rp' + t)

求：(R,t) = argmin 1 / 2 * ∑ || p_i  - (Rp'_i + t) ||²

求质心：

p = 1 / n * ∑(p_i)

p' = 1 / n * ∑(p'_i)

将误差模型改为：

e =  p_i  - (Rp_i' + t)

   =  p_i - Rp_i' - t  (- p + Rp' + p  - Rp')

（红色部分为0）

1 / 2 * ∑ || p_i  - (Rp'_i + t) ||²  

　　= 1 / 2 * ∑ || p_i - Rp_i' - t  - (- p + Rp' + p  - Rp') ||² 

　　= 1 / 2 * ∑ || ( p_i - p - R(p'_i-p') ) +  p - Rp' - t || ²

       = 1 / 2 * ∑ （  || ( p_i - p - R(p'_i-p') ) || ² +  ||p - Rp' - t || ²   + 2 *  ( p_i - p - R(p'_i-p') )^T *  ( p - Rp' - t)  ）

 

1 / 2 * ∑ *  2 *  ( p_i - p - R(p'_i-p') )^T *  ( p - Rp' - t) 

　　= ∑   ( p_i - p - R(p'_i-p') )^T *  ( p - Rp' - t)  ( 看作是常数项，和i无关的)

       =    (p₁ + p₂ +...p_n  - np - R( p'₁+ p'₂ + ...p'_n  - np'  ))^T *  ( p - Rp' - t)    

　　又有（p = 1 / n * ∑(p_i)、p' = 1 / n * ∑(p'_i)）

       =  (0 - 0)^T *  ( p - Rp' - t)

       =  0

 

目标变为：(R,t) = argmin  1 / 2 * ∑ （  || ( p_i - p - R(p'_i-p') ) || ² +  ||p - Rp' - t || ² ) （红色部分既有R也有t）

可以将目标分解，先求 t =   argmin ||p - Rp' - t || ²

 ||p - Rp' - t || ² = -p^Tt + (Rp')^Tt - t^Tp + t^TRp' + t^Tt

 ∂||p - Rp' - t || ² /  ∂t  =   - p + Rp' - p  +  Rp' + 2t                      

　　　　　　　　    = -2p + 2Rp' + 2t

令： ∂||p - Rp' - t || ² /  ∂t  = 0 

得到 :  t = p - Rp'（解算完R后，就可以这样求t）

 将t代入：（R,t）=  argmin 1 / 2 * ∑ || p_i  - (Rp'_i + t) ||²

（R,t）=  argmin 1 / 2 * ∑ || p_i  - (Rp'_i  +  p - Rp') ||²

           =   argmin 1 / 2 * ∑ || p_i  - (Rp'_i  +  p - Rp') ||²

           =   argmin 1 / 2 * ∑ || p_i - p - R(p'_i - p )  ||²

(推到最后，其实就是先通过重心化坐标，干掉t，只剩下旋转了)

那么，令重心化坐标为：

q_i = p_i - p

q‘_i = p'_i - p'

R =  argmin 1 / 2 * ∑ || q_i  - Rq'_i  ||²

|| q_i  - q‘_i  ||² = (q_i  - Rq'_i)^T(q_i  - Rq'_i)

                   = q_i^Tq_i  +  q'_i^TR^TRq'i -  q'_i^TR^Tqi -    q_i^TRq'_i  (  R^TR = I )

                   = q_i^Tq_i  +  q'_i^Tq'i  - 2q_i^TRq'_i 

R =  argmin 1 / 2 * ∑  q_i^Tq_i  +  q'_i^Tq'_i  - 2q_i^TRq'_i 

等价于

R = argmax ∑ q_i^TRq'_i 

补充知识：向量a、b 点积, d是一个数 ：  d =   a^Tb = tr(ba^T) , ba^T是矩阵，d等于这个矩阵的迹

那么：

R = argmax ∑ q_i^T(Rq'_i) 

   = argmax ∑ tr (Rq'_i )q_i^T

   = argmax   tr (R ∑ q'_i q_i^T)

令：  ∑(q'_i )q_i^T =  M^T_3*3

R = argmax tr (R M^T)

找到一个R，使得 tr (R M^T)最大

对M进行分解： M = U∑V^T

 tr (R M^T) = tr(RV∑U^T)

　　　　  = tr(∑U^TRV)   

补充知识：tr(AB) = tr(BA)

补充知识：R是正交，V也是正交，所以RV也是正交

*∑U^T 也是正交

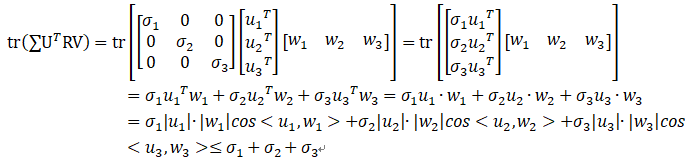
又SVD有如下性质：

 | u_i| = 1、 | w_i| = 1

所以，当 cos<u_i,w_i> = 1，tr(∑U^TRV) 取得最大值 σ₁ + σ₂ + σ₃ 

观测上式：

tr(∑U^TRV)   = σ₁ + σ₂ + σ₃ 

那么：tr(∑U^TRV) = tr(∑ I)   = σ₁ + σ₂ + σ₃ 

当：U^T  = (RV)^T  ， 才有 (RV)^TRV  = I

所以： U = RV

R = UV^T

可以参考：用SVD求解ICP问题的完整证明 - 知乎 (zhihu.com)

---

 

使用李代数迭代求解ICP

p_i = Tp_i'

等价于：

p_i = exp(ξ^)p_i'

e = 1 / 2 ∑ || p_i - exp(ξ^)p_i' ||²

 

 说明：f( x + Δx )在这里是误差函数

 

 

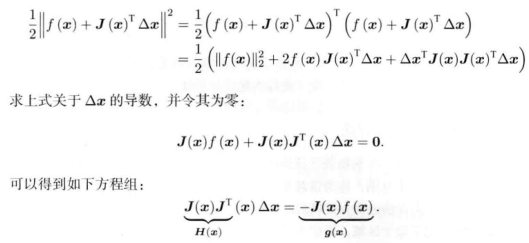
T = ΔTT₀

T = exp(δξ^)exp(ξ₀^)， ξ₀^ 是4 * 4的，δξ、ξ₀ 是 6 *1向量，∂e_i / ∂(δξ)是 4* 6 的

令e_i = p_i - Tp_i'

e_i进行泰勒一级展开：

e_i = p_i - exp(δξ₀^)exp(ξ₀^)p_i'  + ∂e_i/∂(δξ) * Δδξ₀

exp(δξ₀^)exp(ξ₀^) = exp(δξ₀^+ ξ₀^) 

δξ₀ = [0,0,0,0,0,0]^T 

那么：exp(δξ₀^)exp(ξ₀^)  = exp(ξ₀^) = T₀

因此：

e_i = p_i - T₀p_i'  + ∂e_i/∂(δξ) * Δδξ

误差函数：

 f(T)  =   1 / 2 ∑ || p_i - T₀p_i'  + ∂e_i/∂(δξ) * Δδξ₀||² 

 令：f_i  =  p_i - T₀p_i' ，J_i  * Δδξ₀   = ∂e_i/∂(δξ) * Δδξ₀

  f(T)  =   1 / 2 ∑ || f_i  + J_i * Δδξ₀||² 

         =   1 / 2 ∑ (f_i  + J_i * Δδξ)^T(f_i  + J_i * Δδξ)

　　  =  1  / 2 ∑  f_i^Tf_i   + f_i^TJ_iΔδξ₀   +  Δδξ^TJ_i^Tf_i +  Δδξ^TJ_i^TJ_i * Δδξ  

         =  1  / 2 ∑  f_i^Tf_i   +  2 * f_i^TJ_iΔδξ₀   +  Δδξ^TJ_i^TJ_i * Δδξ    

对Δδξ求导，并令其为0：

 ∑ Jf_i + J_i^TJ_i * Δδξ     = 0

 Δδξ  * ∑ J_i^TJ_i       =  - ∑ Jf_i 

解得  Δδξ

δξ = δξ₀ + Δδξ = [0,0,0,0,0,0]^T + Δδξ = Δδξ

T = ΔTT₀ = exp(δξ^)exp(ξ0^) 

继续迭代

---

 

补充知识

 

 

 

 

 

---