非线性优化

参考： 卡尔曼滤波（一） - 耀礼士多德 - 博客园 (cnblogs.com)

参考：相机模型 - 耀礼士多德 - 博客园 (cnblogs.com)

卡尔曼滤波模型有两条方程：

1. 运动方程：x_k = f(x_k-1,u_k) + w_k 。 u_k是系统控制量，有可能是常数、w_k 是过程噪声服从高斯分布

2. 观测方程：Z_k,j = h(y_j,x_k) + v_{k,j 。} 观测方程。v_k,j  是测量噪声

V_k ~ N(0, Q_kj) ： V_k 服从 均值为0 ， 协方差矩阵为Q_kj 的高斯分布，下标为kj ，因为每个时刻k，测到每个点j，都对应一个Q

---

 对于【观测方程】，可以以一张照片的【针孔模型】为例：

如果测量无误差，即v_k,j = 0，有：

Z_kj = K(Ry_j + t_k)

Z_kj 为点在照片上的坐标，可以由Z_kj = s * z_k,j  , z_k,j 为像素的索引，s为像素的长或宽

K是内参矩阵

R是旋转矩阵

t_k是平移向量

y_j是已知点，或者叫【路标】、【控制点】（可以由GPS，全站仪等设备给出）

(R_ky_j + t_k) = Ty_j , T是欧氏矩阵，表示相机位姿。

那么，x_k = T_k ,也就是说，相机的【位姿】就是要估计和优化的对象。

---

 估计T_k，通常有两种方法：

1. 使用卡尔曼滤波。特点：不用采集所有数据，每次都估计【最后一个T】，用于实时估计

2. 使用【批（batch）】处理法。类似于平差，最小二乘整体求参，能得出【每个T】，用于采集后估计。

---

 假设从1到N，有：

1. 机器人【位姿】x = { x₁,......x_n }

2. 已知点【坐标】y = { y₁,......y_n }

---

 贝叶斯公式

 P(A | B)， 在B事件已发生的情况下，发生A事件的概率。

那么：P(A | B) = P( B |A ) *P ( A ) / P( B )

由来：P(A∩B) = P(A) * P(B | A) = P(B) * P( A | B) ， P(A∩B)  = AB同时发生的概率 ：

1. AB同时发生的概率= A发生的概率 * A已发生的情况下B发生的概率

2. AB同时发生的概率= B发生的概率 * B已发生的情况下A发生的概率

---

 P( x,y | z, u )的意思是，在已知观测数据 z ( 点在相片上的位置 )、u（可能是常数）时，控制点坐标  & 相机位姿的概率分布函数。

（如果没有u，就写成 P( x,y | z））

使用【贝叶斯公式】：

 （是不是因为z,u是实际得到的，所以概率为1？？？）

关于先验后验

 

 

 

 

---

argmax 函数，当我们有另一个函数y=f(x)时，若有结果x0= argmax(f(x))，则表示当函数f(x)取x=x0的时候，得到f(x)取值范围的最大值

 

---

(x,y)*_MAP =  argmax P(x,y | z, u) 翻译：

1  .  第一个等号，当  【位姿、路标是(x,y)*_MAP   】时， 概率分布函数P取得最大值。

2  .  第二个等号，在什么样的 位姿、路标下，最有可能得到这样的观测数据

 后验概率最大化下，求得位姿

---

 Z_k,j = h(y_j,x_k) + v_k,j 

因为 ：V_k ~ N(0, Q_kj)

所以： P(Z_k,j  | y_j,x_k)  = N( h(y_j,x_k) , Q_kj)

翻译：

1. P(Z_k,j  | y_j,x_k) ， 在位姿为X_k, 控制点坐标为y_j的情况下，控制点在照片位置Z_k,j  的概率

2. Z_k,j  的 均值是h(y_j,x_k) ， 其方差和V_k 方差一样，等于Q_kj

k时刻，j点在照片中的位置：Z_k,j  = [u_kj,v_kj] ^T

 

---

 

任意维度的高斯概率分布函数 z ~ N ( μ , ∑) ，  z、μ , ∑，都是矩阵形式

(7 封私信 / 80 条消息) 多维高斯分布是如何由一维发展而来的？ - 知乎 (zhihu.com)

高位高斯分布的推算，还用到：

1. 主成分分析：测绘线性代数（四）：数学期望、协方差、PCA - 耀礼士多德 - 博客园 (cnblogs.com)

2. 主成分分析，主要目的是【去相关】，然后就可以用相互独立的观测量推算高维高斯分布，到最后【回代】就可以了。

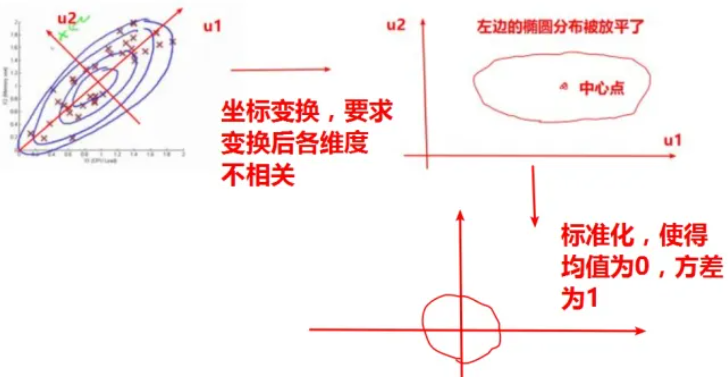
高维高斯概率分布密度函数

---

 

按照【高维高斯概率分布密度函数】的理解：

 ∑  = Q_kj

 要求得P( z )的最大值时，对应的X_k ，翻译：

1. 求得什么样的X_k ，使得 z = z的概率最大。

2. 求得什么样的位姿，使得得到观测值Z 的概率最大。

---

对【高斯概率分布密度函数】，进行变换：

 

 

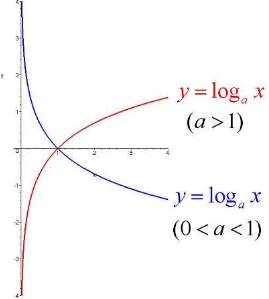
 a = e > 0

所以 ln(P(x)) 是单调递增（红色）

求P(x)最大化，相当于对 ln(P(x)) 求最大化

 对 ln(P(x)) 求最大化，相当于对 - ln(P(x)) 求最小化

 

 【要求得P( z )的最大值时，对应的X_k  】（数学语言：x = argmax(P(z))），转化为：

1 .用高斯概率分布密度函数解析，求得 - ln(P(x)) 最小化时，对应的X_k ，数学语言 Xk  = argmin( - ln(P(x)))

2 . 对于上式，1 / 2 * ln( (2π)^Ndet(∑)) ，和X_k  无关  ，因此，转化为：

3. 用高斯概率分布密度函数解析，求得 (x - μ)^T∑^-1(x - μ) 最小时，对应的X_k  ，这里的∑对应的是Q_kj

4. 最终问题为，求得位姿 X_k ， 使得(x - μ)^T(Q_kj)^-1(x - μ) 最小，数学语言 x_k = argmin [  (x - μ)^TQ_kj(x - μ)  ]

5. 最终结果，求得位姿 X_k  = argmin[ (z_k,j - h(y_j,x_k) ) ^T (Q_kj)^-1   (z_k,j - h(y_j,x_k) )   ]

  

---

 (z_k,j - h(y_j,x_k) ) ^T (Q_kj)^-1   (z_k,j - h(y_j,x_k) )  

 令：

e_n*1 =  z_k,j - h(y_j,x_k)  =  [e₁,e₂,e₃...] ^T

  E_1*1 =  (z_k,j - h(y_j,x_k) ) ^T (Q_kj)^-1   (z_k,j - h(y_j,x_k) )   = e^T  (Q_kj)^-1 e

(E 就是一个二次型，由e₁² 、e₂² 、e₃² 组成)

记住：最终问题为，求得位姿 X_{k ，}使得E最小

 （答案： X_k = (H^T∑^-1H)^-1H^T∑^-1y，測量平差中的加权最小二乘法）

注意：H是h(y_j,x_k) 关于x_k的系数矩阵，y是将x_k 线性化后的常数列向量

---

简单线性系统：

模型：

x_k = x_k-1 + u_k + w_k    w_k ~N(0,Q_k)  :  w_k 是误差，服从正态分布

Z_k = x_k + v_k   V_k ~N(0,R_k)      :  V_k 是误差，服从正态分布

误差方程：

e₁ = x_k - x_k-1 - u_k ,  注意到，如果按照模型方程，wk应该写在括号左边，但是e和w是不同的概念，w相当于是一个象征，而e是可以最终回代计算出来的

e₂ = x_k - z_k 

 假设有时间k = 1,2,3  ,  X₀已知（注意），那么有：

x = [ x₀,x₁,x₂,x₃ ]

z = [ z₁,z₂,z₃ ]

u = [ u₁,u₂,u₃ ]

还有对应的协方差阵 Q₁，Q₃，Q₃， R₁，R₂，R₃

 那么，其实就是要求得 x₁, x₂ ,x_{3 ，}使得以下概率最大：

 

 

 （回顾上面的高维高斯分布）

 等价于：

 求得 x₁, x₂ ,x_{3 ，}使得以下值最小：

 f =  ∑e₁ ^TQ_k^-1e₁  + ∑e₂ ^TR_k^-1e₂ 

 要求得这个结果:

1 . 其实就是解线性方程组的【加权最小二乘解】：

0 = x_k - x_k-1 - u_k  

0 = x_k - z_k 

( 假设e = 0的解，实际上e不为0，当时强行解，就得到最贴合的 x = argmin( f ) 的解)

令： y = [u_{k ,} z_k] ^T

 

 

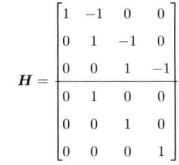
 （注意，如果x₀是已知的，那么H第一列应该去掉，同时 y_1,1 = u_k - x₀）

那么，原式子为：

e = y - HX   e~ N(0,∑) 

∑ = diag ( Q₁，Q₃，Q₃， R₁，R₂，R₃)， diag()是使用Q₁，Q₃，Q₃， R₁，R₂，R₃ 形成对角矩阵或对角分块矩阵

 注意：f也要重新写成矩阵形式

2 .  使用矩阵求导：  ∂f / ∂x = 0，得到f的极小值时的X_4*1

 ∂f / ∂x = H^T∑^-1e  =  H^T∑^-1(y - HX) = 0  等价于 ：H^T∑^-1HX    =  H^T∑^-1y （  可以看成 Ax = b，直接高斯消元法解，没必要求逆浪费算力 ）

3. 最终得到：X  = (H^T∑^-1H)^-1H^T∑^-1y 

 

---

 迭代解法

一阶&二阶梯度法

假设观测方程：

Z = G(X) + U（Z为观测值）

可以转化为误差方程：

E = F(X) = G(X) + U - Z

目的：求得ΔX = argmin(F(X))，注意，整个目标，与要求概率Δx = argmax(P(z))，之间差了一个∑：

Δx = argmax(P(z)) 转化为 Δx = argmin( e^T∑e)，也就是Δx = argmin( F(X)^T∑F(X))

 假设有误差方程：

y_m*1  = F(X) （如果是泰勒一阶展开线性化后，就为  y_m*1 = A_m*nX_n*1 + y₀）

 要求得X ， 可以令 X = X₀ + ΔX ， X₀可以通過其他手段，例如：估算，或从其他一个观测方程中得到近似值，属于【已知的常数】

 那么，原问题变为：

F(X) = F(X₀ + ΔX)  

对F(X)进行泰勒二阶展开

F(X)  ≈ F(X₀) + J(X)(X - X₀) + 1 / 2 * (X - X₀)^TH(X) (X - X₀)

因为 ΔX = X - X₀

F(X)  ≈ F(X₀) + J(X)ΔX + 1 / 2 * ΔX^TH(X) ΔX

y_m*1 = [f₁(X),f₂(X),.....f_m(X)]^T

拿其中一条式子来拆分分析

J₁ = [∂f₁ / ∂x₁ ,  ∂f₁ / ∂x₂ ....∂f₁ / ∂x_n]   为 1 * n

ΔX = [Δx₁ ,  Δx₂ ....Δx_n]  为 n * 1

H₁ 为 n * n 

 

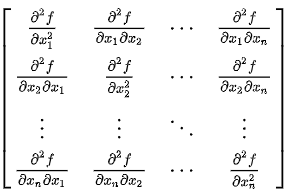
y₁ ≈  f₁(X₀) + J₁ΔX + ΔX^TH₁(X) ΔX

整个式子分析

 F(X)  ≈ F(X₀) + J(X)ΔX + 1 / 2 * ΔX^TH(X) ΔX

 J(X)为【雅可比矩阵】(一阶导数阵)：

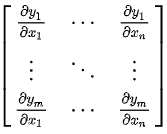（对X进行偏导，然后式子再用X₀代入，得到的其实是X₀处的斜率）

 J为 m * n

 H(X)为【海塞矩阵】(多维函数二阶偏导)：

H(X) 为分块矩，对角线上分别为一个H_n(X) ，每条方程的海塞矩阵

H(X) 为n * n * m 行和 n * n * n 列

 

---

 ΔX = argmin(F(X)) 方法一：

 F(X)  ≈ F(X₀) + J(X)ΔX + 1 / 2 * ΔX^TH(X) ΔX

 ΔX =  argmin(F(X)) ≈  argmin(F(X₀) + J(X)ΔX + 1 / 2 * ΔX^TH(X) ΔX)

 等价于 

  ΔX = argmin( J(X)ΔX + 1 / 2 * ΔX^TH(X) ΔX）

 那么，对J(X)ΔX + 1 / 2 * ΔX^TH(X) ΔX 求关于ΔX的导数，并令其为0，得到F(X)的极小值，得到：

 J(X) + H(X) ΔX = 0 

 ΔX = H^-1(X)J(X)

证明： ∂(X^TA X) / ∂X = 2AX

f(X) = X^TA X , 是1*1的

 

 

 根据【函数对向量求导】：∂ f(x) / ∂ X_n*1 是 n * 1 的

 

 

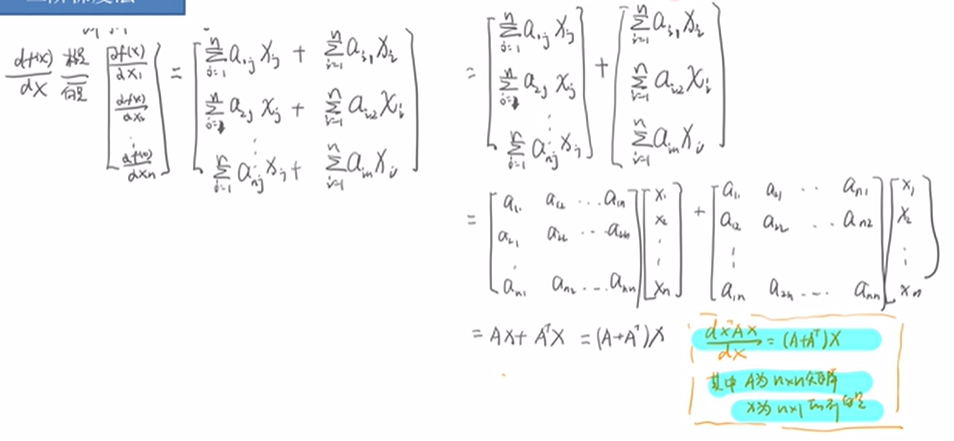
 ∂(X^TA X) / ∂X =(A+A^T)X

因为A是对称的，所以 ∂(X^TA X) / ∂X =(A+A^T)X = 2AX

 

 (注意，实际很少使用这个，因为【海塞矩阵】比较不好求)

---

 

 X = argmin(F(X)) 方法二：

仅仅进行一阶展开：

 F(X)  ≈ F(X₀) + J(X)(X - X₀)

 求 ΔX =  argmin(F(X)) ，等价于求：

 ΔX =  argmin [ 1 / 2 (F(X₀) + J(X)(X - X₀) ) ²] 

 （之所以这样，是为了后面求导公式消去2）

 

 

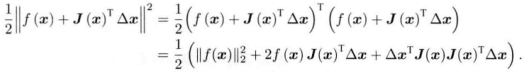
 然后求关于ΔX导数，并令其为0

 

 

唯一要求是J列独立，那么  JJ^T才可逆， ΔX 唯一

---

 

证明：J列线性无关，JJ^T可逆

J列独立，  JΔX=  0 ，ΔX有非零解

(JΔX)^TJΔX = 0 

ΔXJ^TJΔX = 0

ΔX^TJ^TJΔX = 0 

ΔXJJ^TΔX = 0

JJ^TΔXJJ^TΔX = 0

JJ^TΔX = 0

因为ΔX有非零解，所以JJ^T列线性无关，列线性无关的方阵是可逆矩阵

 

---

 有时候J可能会病态，每次解算出的ΔX都大，导致X不容易收敛。

（J病态通常是控制点分布过于集中，导致多行近似线性相关）

 衡量ΔX 好坏的指标

ρ  = 误差函数实际下降的值  / 模型下降的值

ρ  = [ f(X + ΔX) - f(X) ] / J^TΔX

ρ  越接近1 ，证明使用这个模型来算，与实际得出的结果越相符

改进版线性优化步骤

 

 

 注解：

1. D_n*n为系数矩阵，应该是对ΔX_n*1进行加权用的，通常为 I，或者非负的其他对角阵（能不能用Σ求得权阵用呢？）

2. || D_n*n ΔX_n*1||² 是一个距离平方，那么ΔX₁²  + ΔX₂² +ΔX₃²  + ...≤ μ   (X如果是位姿，那么就是 1″，1mm之类的经验值，限制∑ΔX_i² 不能太大)

 

有没有办法没有那么啰嗦？

条件极值杀手——拉格朗日乘数法 - 知乎 (zhihu.com)

准备知识：

此处的拉格朗日函数：

 

 对£进行关于ΔX的导数，并且∂£ / ∂ΔX = 0，得到：

(H +  λD^TD)ΔX = g (g往上翻能看到)

解得ΔX

---

 

 

 

 

 

 

 

 

 

nm