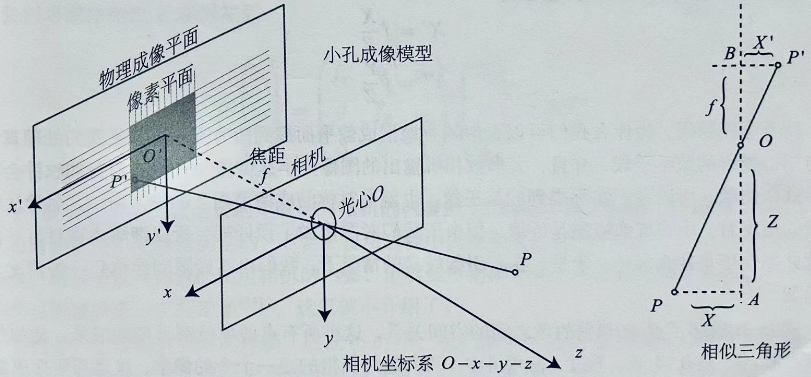
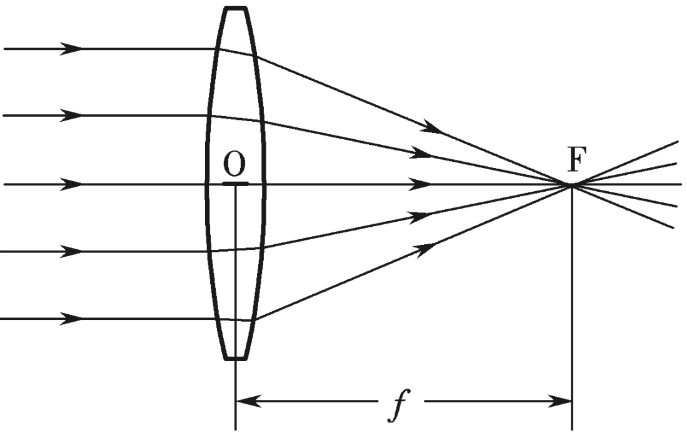
相机模型
坐标系定义：
1. 以相机光心为原点
2. 垂直于像素平面方向为Z轴
3. 平行于像素水平排列方向为X轴
4. Z x X 为Y轴，叉积
P点的坐标：
1. 像面 [X', Y', Z']T
2. 实物 [X , Y, Z ]T
(注意：Z不是垂直方向的，并且注意到坐标系的定义方式)
因为相机会自动将照片翻转，所以根据相似三角形原理，可以得到：
f = Z / f = X / X' = Y / Y'
X' = f * X / Z ....................(1)
Y' = f * Y / Z ....................(2)
又由于，像素坐标系，通常是：
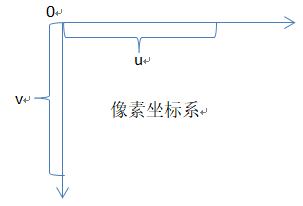
那么又有如下公式：
u = α X‘ + cx ........................(3)
v = β X‘ + cy ........................(4)
u，v大于0，而且是整数，而X’、Y'就不一定大于0了，也不一定是整数
（在原来相机坐标系下缩放、平移，最终成了相片）
每个相机应该都是可以输出不同大小尺寸的照片的
将（1）、（2）代入（3）、（4），得到：
u = α * f * X / Z + cx
v = β * f * Y / Z + cy
令：
fx = α * f（横向缩放比例 * 焦距）
fy = β * f（纵向缩放比例 * 焦距）
则：
u = fx * X / Z + cx
v = fy * X / Z + cy
写成矩阵形式：
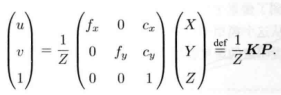
等价于：
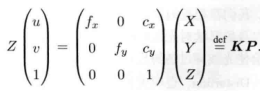
K ， 就是【内参矩阵】
总结：
1. K其实内容是α、β、f、cx、cy。
2. cx、cy理论上是 - W / 2，- H / 2，因为原点挪到左上角了，W，H是横向像素个数与纵向像素个数。
3. K需要标定，因为仅仅靠出厂提供的参数，会随时间发生不准。
4. P是相机坐标系下，实物的坐标(X,Y,Z)T
已知：
【相机坐标系】下P点坐标：P = (X,Y ,Z)
【世界坐标系】下P点坐标：Pw = (Xw,Yw,Zw)T
【像平面坐标系】下P点坐标：Puv = (u,v,1)T
P = RPw + t
那么，有：
ZPuv = KP = K(RPw + t)
R3*3为【旋转矩阵】
t3*1 为【平移向量】
因为RPw + t ，可以写成特殊欧式阵T4*4：
那么：
ZPuv = KP = KTPw
注意：T不是欧氏矩阵，而是一下形式，结果与 K3*3(R3*3Pw + t) 是一致的
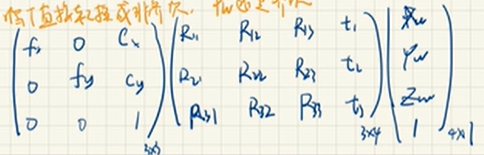
注意：也可以将T写为4*4的欧氏矩阵， Pw写为4*1，乘完之后选前3行，再与K相乘
R，t又称为相机的【外参】，旋转 + 位移，合称【位姿】
总结：
1. P在相机坐标系下坐标（X,Y,Z），每个P点的Z其实都是一样的，因为都在一个平面上
2. 仅仅凭借一张照片(u,v)、K、R、t， 依然是缺少了Z值，根据式子，也没办法得到Pw
镜头畸变
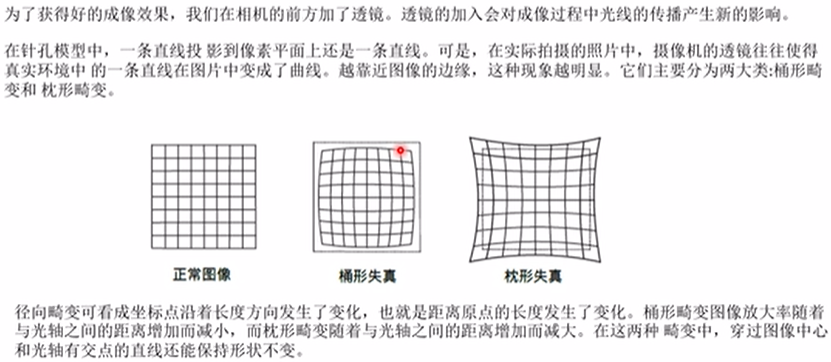
假设P点在像面上，以光心垂直投影为原点，其坐标为x,y ， 写成极坐标，为(θ, r)
径向畸变模型：
切向畸变模型：
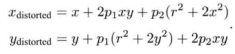
综合起来：
问题：
1. 如何求k1\k2\p1\p2
2. 猜想：
1. 使用已知x,y的点，例如十字标靶，但是要归一化，变成相机坐标系下x,y
2. 拿这些点最小二乘解得参数
nm
