矩阵函数

普通函数

f(x) = x + 2

 

要点：不要将F(x) 当成是 Fx

F是函数，或是多个函数，多个函数就可以写成矩阵的形式：

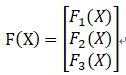
而X可能是向量，也可能是矩阵

 F(X)，就是每个函数，都要作用到每个X，每个X的各个元素，都要，若 f_m*n ，那么输出也是m*n的矩阵

例如：

 

 

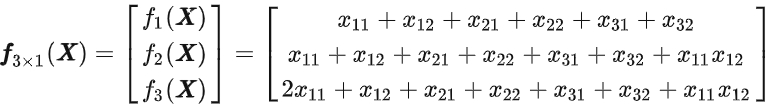
例如：

 

---

 

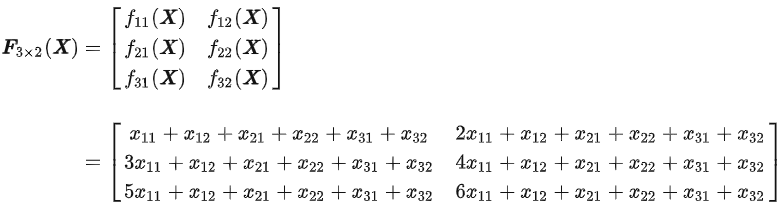
x =  (x₁,x₂,x₃)^T

求导

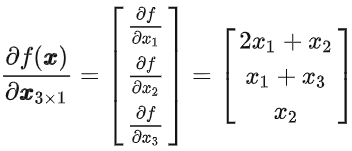
求微分

 

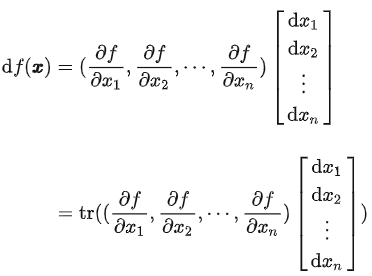
（注意：矩阵微分，可以用矩阵求迹来表达）

---

 

 

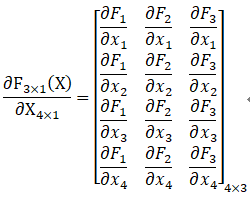
 （注意，这种方式应该是没有的，瞎搞）

只有一下两种方式

分母是行，分子是列（1）

 

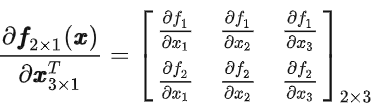
分母是列，分子是行（2）

 

 

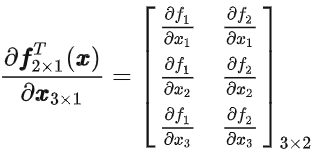
分母是单个函数，分子是矩阵

求导

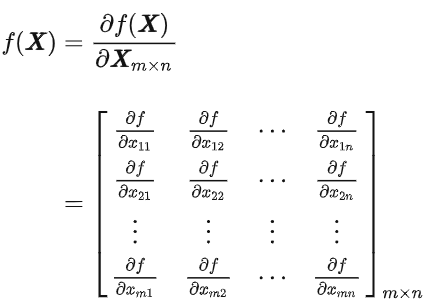
求微分：

 

（注意：矩阵微分，可以用矩阵求迹来表达。为了写得更加好看一点）

分子是矩阵，分母也是矩阵

先将X转化为向量

 

 也将F转化为向量

 

 

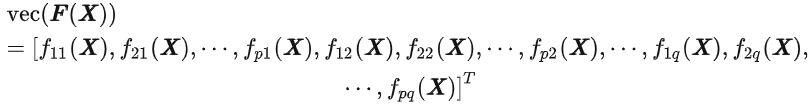
 那么，可以利用（1）来求导

 形状： pq x mn

 求微分：

 

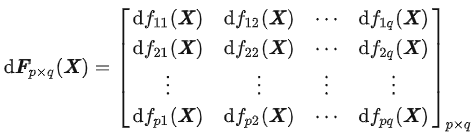
 （注意，例如 df₁₁(X) , 按照上面 f'(x) = ∂f(X)/∂X_mxn 的例子来算）

 

---

 

求导法则1

 

 

 

求导法则2

 

 

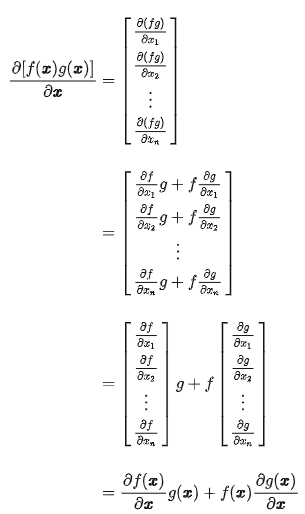
求导法则3

 

 

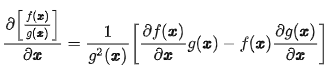
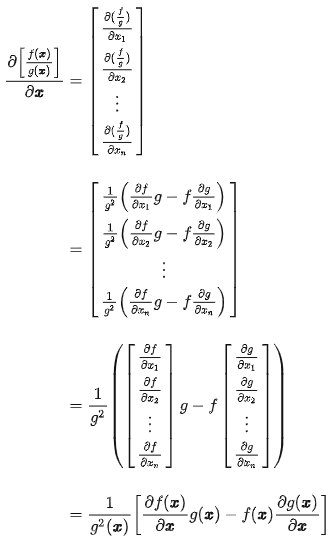
参考：矩阵求导公式的数学推导（矩阵求导——基础篇） - 知乎 (zhihu.com)

---

求导快捷式

 

 

 

这个有点意思

 

 

 

 求到最后，整理一下，可得。结论：直接按【分母是行，分子是列】方式求

---

 矩阵的迹

参考：矩阵求导公式的数学推导（矩阵求导——进阶篇） - 知乎 (zhihu.com)

（一）

 

 （方阵才有迹）

（二）

 

（三）

 

 

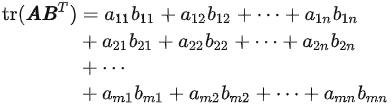
 （四）

 ，

 （五）

---

 微分法则1

 

 

  微分法则2

 

  微分法则3

---

 

最终，使用求矩阵求微分，可以更加直观的求导

例如：

F_1x1 , X_mxn

 

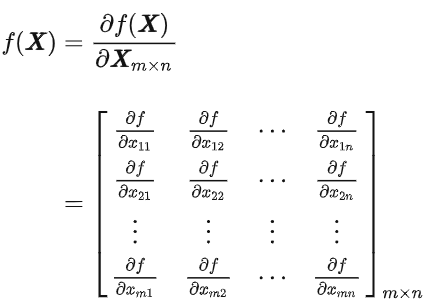
 tr()中，左边其实就是导数 ∂f(X) /∂X^T_mxn , 对X转置求导

d(fx) = tr( ∂f(X) /∂X^T * dX )

 

 

先了解一个性质：

d(AXB) = Ad(X) B

A_pxm ,  B_nxq, X_mxn , A、B为常数矩阵

由微分法则二得：d(AXB) = d(A)XB + Ad(X)B + AXd(B)

由于AB是常数矩阵，所以：dA = 0_pxm , dB = 0_nxq

证毕。

 

X_mxn 可以代入矩阵函数 ，

矩阵函数的结果是矩阵，例如：F(X) = X^TX

普通函数，就例如：f(X) = x₁*x₁ + 2x₂ + 3x₃

 

 

使用矩阵微分求导

对于形如：f(X) = x₁*x₁ + 2x₂ + 3x₃

1.  tr(f(X)) = f(X)

2.  df(X) = tr(df(X))，因为 df(x) = a +b +c , tra(a+b+c) = a+b+c