几种特殊的矩阵和用途(一)
(一)协方差矩阵——过渡矩阵
已知协方差矩阵:
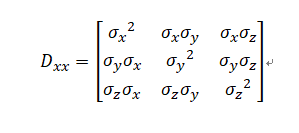
这里是 1 / n,属于有偏估计
![]()
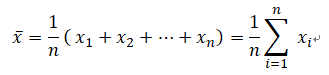
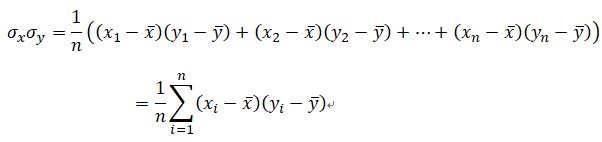
过渡矩阵:
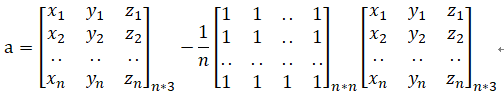
![]()
(二)二次型
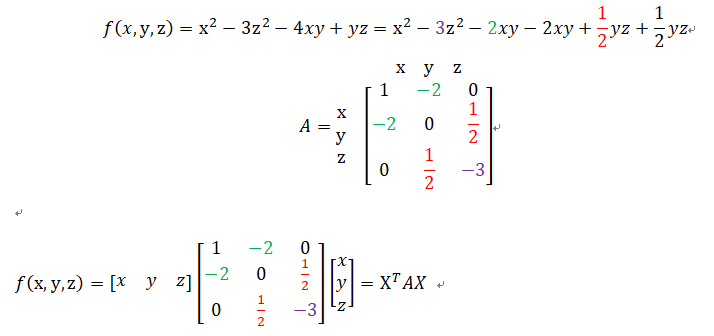
用处1:基变换,P是其他坐标基
(P是单位正交矩阵,在世界坐标系下的向量,相当于XYZ轴旋转后,在【自然坐标系】下的单位向量)
![]()
(单位正交矩阵的逆矩阵,就是其转置,P-1 = PT)
所以:
f(x',y',z') = X'T PTAPX'
B = PTAP
B又叫合同矩阵,与A合同。
(x',y',z')已经不是【自然坐标系】下的坐标了。
用处2:旋转
直接将PTX代替X,f(x,y,z) = XT PTAPX,(x,y,z)依然是【自然坐标系】下的坐标。
(三)坐标基
第一阶段:
自然坐标系下,测得:A、B、C 、P1、P2、P3三维坐标
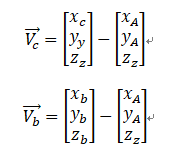
令:
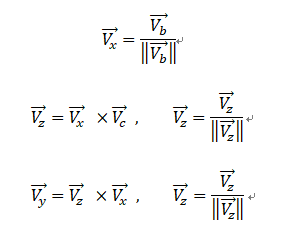
P1、P2、P3 在ABC坐标系下坐标:

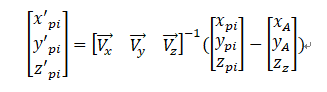
第二阶段:
自然坐标系下,测得:
A、B、C ,不能测得P1、P2、P3,求P1、P2、P3在自然坐标系下的坐标
假设A的坐标,带“_”号
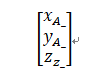
得到三个正交单位向量
![]()
P1\P2\P3在ABC下的坐标不变,依然为:
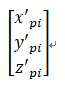
P1、P2、P3的自然坐标,为:
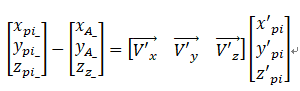
![]()



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 分享一个免费、快速、无限量使用的满血 DeepSeek R1 模型,支持深度思考和联网搜索!
· 基于 Docker 搭建 FRP 内网穿透开源项目(很简单哒)
· ollama系列01:轻松3步本地部署deepseek,普通电脑可用
· 按钮权限的设计及实现
· 25岁的心里话