积分学习笔记
极限的数学表达
∀:任意,Any
∃:存在,总是可以找到,Exist
极限的定义:
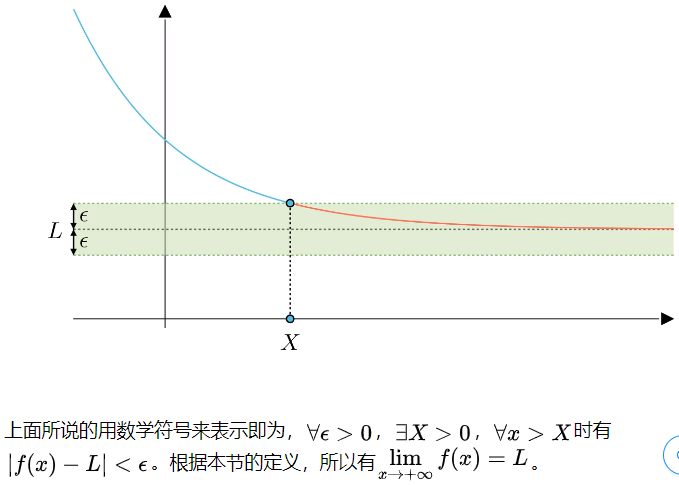
理解:
1. 在Y轴上,任意的ε 范围内
2. 总是可以找到能找到 X > 0
3. 满足1、2条件时,对于所有的 x , x大于 X 时
4. 如果有 | f(x) - L | < ε
5. 那么 lim f(x) = L,或者叫f(x)收敛于L
求导的本质:求极限
假设:
距离解算公式:
![]()
在 t = 2处的导数,也就是t = 2处的速度
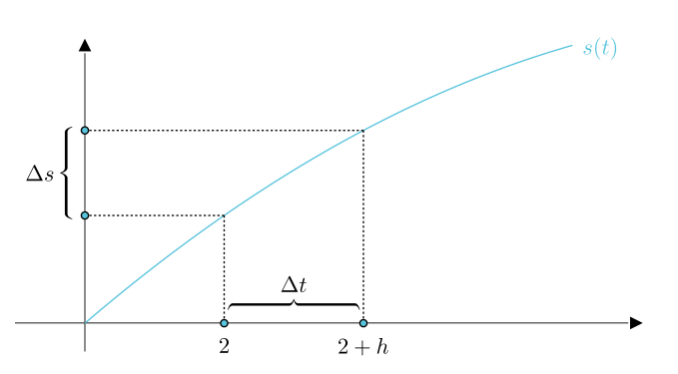
[ 2, 2 +h ]的平距速度
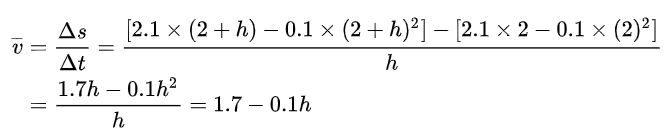
(h不能真的等于0,否则就违反为数学规则,只能 h -> 0)
lim (1.7 - 0.1h) = 1.7,(h->0)
验证:
1. 公式求导:s'(t) = 2.1 - 2 * 0.1 * t
2. 代入t = 2时,s'(t) = 1.7
总结:
1. 先假设t = a, avg = [ s( a + h ) - s(a) ] / h
2. 求 lim avg ,( h - >0 ),即可得到导数
y = f(x)
![]()
lim (Δy /Δx) = lim [ (f (x + Δx ) - f(x) ) / Δx ] = dy / dx = f'(x)
f'(x0),就是在x = x0处切线的斜率
dy = f'(x) dx 含义:y的改变量的【近似值】等于【x处的斜率】 乘上x的改变量
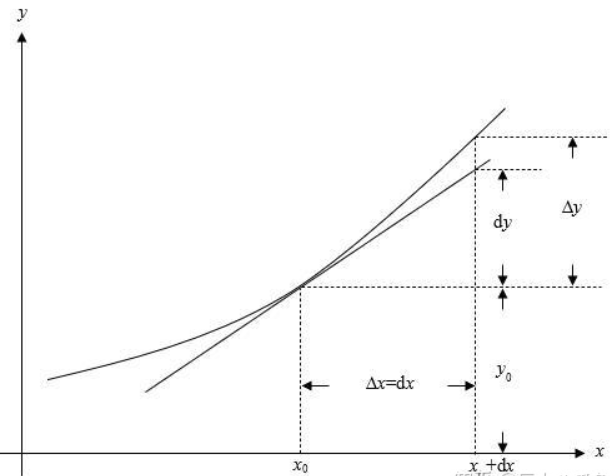
注意:
1. x最终是有实际意义的,比如在x = 1附近求导
2. Δx是代数,最终是要消去的(Δx趋向于0,或等于0来消去)
复合函数微分
y = f(u) , u = g(x)
dy = d [ f(u) ] = f'(u) du = f'(u) d[g(x)] = f'(u) g'(x) dx
例如:
y = sin(2x + 1) , u = 2x + 1
dy = d [ sin(u) ] = cos(u)du = cos(2x+1)d(2x +1 ) = cos(2x+1) * 2dx
多元函数全微分
z = f( x, y)
![]()
注意,这里加入了∂号,专门特指偏导
偏导:例如 ∂z / ∂x,就是将y当成常数,对x进行求导
复合多元函数全微分
![]()
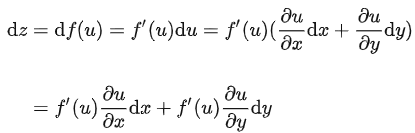
例如:
![]()
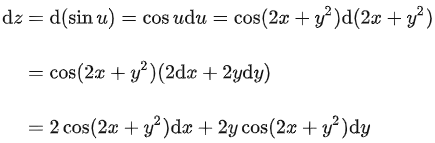




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 分享一个免费、快速、无限量使用的满血 DeepSeek R1 模型,支持深度思考和联网搜索!
· 基于 Docker 搭建 FRP 内网穿透开源项目(很简单哒)
· ollama系列01:轻松3步本地部署deepseek,普通电脑可用
· 25岁的心里话
· 按钮权限的设计及实现