卡尔曼滤波（七）——非线性系统

非线性系统卡尔曼滤波，又叫“扩展卡尔曼滤波”

模型公式：

X_k=AX_k-1+BU_k+W_k-1 

Z_k = HX_k + V_k

p(w) ~ N(0,Q)

p(v) ~ N(0,R)

 

预测：

先验值：X^-_k = AX^{^}_k-1 + BU_k-1 

先验协方差：P^-_k =  A P_k-1 A^T   + Q_k-1

 

校正：

卡尔曼增益：K_k = P^-_kH^T / (HP^-_kH^T +  R)

后验值：X^{^}_k = X^-_k + K_k (Z_k - HX^-_K)

后验协方差：P_k = (I - K_kH)P^-_k

---

 

对于非线性系统，没办法用【X_k=AX_k-1+BU_k+W_k-1 】表达

只能表达成：x_k = f(x_k-1,u_k-1,w_k-1)

z_k = h(x_k,v_k)

p(w) ~ N(0,Q)

p(v) ~ N(0,R)

 

正态分布的随机变量，通过非线性系统后，就不是正态分布了。

线性正态分布：

 

 y = kx，x正态，y也是正态

非线性正态分布：

y = f(x) 

 

 

---

 

线性化，泰勒一阶展开（当X₀非常接近要求的X时，而X不可知，所以X₀ 相当于初始值，靠猜或用低精度仪器测，但是不能太离谱）：

f(x)  = f(x₀) + δf / δx ( x - x₀)

对于高维度，要用到【雅可比矩阵】

 

 

 

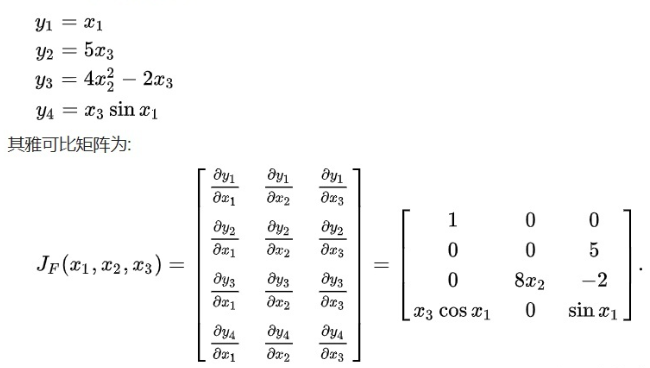
 f(x)  = f(x₀) + J*(X-X₀)

---

 

 对于模型来说，X_k = f(x_k-1,u_k-1,w_k-1) 泰勒展开：

那么，使用X_{k 初始值}  = X^{^}_k-1   (第K-1次后验值)

 X_k = f(x^{^}_k-1,u_k-1,w_k-1) + J (X_k - X^{^}_k-1) + W_kW_k-1

疑问：按照泰勒公式，为不是J (X_k-1 - X^{^}_k-1)？？难道是X_k-1 - X^{^}_k-1 与X_k - X^{^}_k-1 相当接近？？

疑问：W_kW_k-1 是怎么来的？这个是对W_k-1进行求导的项，在W=0处对W_k-1的偏导

 理解起来 

1.  f(x^{^}_k-1,u_k-1,w_k-1)  为 f(x₀)

2.  J (X_k - X^{^}_k-1) 应该为 J (X_k - X_k初始值 )

3. J = δf / δx，将(X^{^}_k-1 , U_k-1 代进去）

 

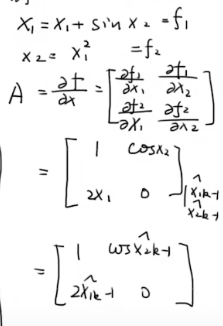
 4. 那么J，或者A矩阵，每一步都是变化的，每次都要重新算。

因为w_k-1 一般不可以知道，假设为0，那么：

 

X_k = f(x^{^}_k-1,u_k-1,0) + J (X_k - X^{^}_k-1) + Ww_k-1

 

同理，对于【Z_k = HX_k + V_k】，令X^~_k = f(x^{^}_k-1,u_k-1,0) ，因为模型算出的X^~_k  ，比起X^{^}_k-1更加接近真实的X_k

Z_k = h(X_k , V_k)

Z_k =  h(X^~_k,0) + H (X_k - X^~_k)  + Vv_k

H = δh / δx (用X^~_k 代 X_k)

V = δh / δv (用X^~_k 代 X_k)

 令：Z^~_k = h(X^~_k,0) 

整理，得到：

X_k = X^~_k + J (X_k - X^{^}_k-1) + W_kw_k-1

Z_k =  Z^~_k  + H (X_k - X^~_k)  + Vv_k

 

p(w) ~ N(0,Q)

p(Ww) ~ N(0,WQW^T)

---

 

预测：

X^-_k = f( X^{^}_k-1 , u_k-1,0)  

P^-_k= A P_k-1A^T + WQW^T

 

矫正：

K_k = P^-_k H^T / (HP^-_kH^T + VRV^T)

X^{^}_k = X^-_k + K_k(Z_k - h(X^-_k,0))

P_k = (I - K_kH) P^-_k