卡尔曼滤波（六）——二维例子

一维例子

使用尺子测量一段距离：

Z₁ = 6.5mm，σ₁ = 0.2mm 

Z₂ = 7.3mm，σ₂ = 0.4mm 

如何求最优估计？

根据模型：

X_k=AX_k-1+BU_k+W_k-1 

Z_k = HX_k + V_k

Q =E(WW^T)= E( [w₁,w₂]^T [w₁,w₂] )。

理解办法：

1. 认为 【一段距离】的长度是恒定的，因此，X_k=X_k-1 ，那么A = 1

2. 因为X_k 为固定的【一段距离】，而Z_k又恰好是这段距离，中间没有转换，所以 H =1

 

预测：

先验值：X^-_k = AX^{^}_k-1 + BU_k-1 

先验协方差：P^-_k =  A P_k-1 A^T   + Q_k-1

令 H = 1：

问题：X^-₂ =  X^{^}₁ ，问题： X^{^}₁ 等于多少？

答：X^{^}₁  = 6.5mm ，只能从k =2开始算，而k =1时，只能拿测量值当后验值用。

 

根据：先验协方差：P^-_k =  A P_k-1 A^T   + Q_k-1，A = 1 ，K =2 ，得：先验协方差：P^-₂ =  P₁   + Q₁

问题：Q₁是多少？

答：Q₁为过程误差协方差， 这里不认为有模型误差，Q₁= 0。因为X^{^}₁ 是直接估计的，所以不存在过程误差。  所以：P^-₂ =  P₁ 

又P₁ 是后验协方差矩阵，k =1时，只能拿测量值当后验值用，所以P₁ = 0.2²

 

【预测】整理：

X^-₂ =  X^{^}₁ = 6.5

P^-₂ =   P₁ = 0.2²

 

校正：

卡尔曼增益：K_k = P^-_kH^T / (HP^-_kH^T +  R_k)

后验值：X^{^}_k = X^-_k + K_k (Z_k - HX^-_K)

 

【预测】整理：

K₂ = P^-₂ / (P^-₂ +  R₂)  （观测值协方差阵： R = E(VV^T) = E( [v₁,v₂]^T [v₁,v₂] )）

R₂ = 0.4²    （测量值协方差：R = E(VVT) = E[ [v₁,v₂]T [v₁,v₂] ]）

K₂ = 0.2² / (0.2² +  0.4²) = 0.2

最优估计：

X^{^}₂ =  6.5 + 0.2² / (0.2² +  0.4²) * （ 7.3 - 6.5 ）= 6.66m

后验协方差：P_k = (I - K_kH)P^-_k

P₂ = （1 - 0.2）* 0.2² = 0.032

 

---

 二维例子

假设一个人在走路，那么有如下状态：

x₁：位置

x₂：速度

有如下条件：

1. 速度假设是恒定的。（实际上不会匀速）

 

那么，模型方方程【X_k=AX_k-1+BU_k+W_k-1 】，可以写成如下：

x_2,k = x_2,k-1 + W_2,k-1

x_1,k = x_1,k-1 + ΔT * x_2,k-1 +  W_1,k-1

ΔT ：采样间隔，k时刻与k-1时刻的间隔，令ΔT=1（如何保证ΔT每次都是1是个难题）

W：过程噪声，可能地面有石头，有上下坡，导致速度不能完全匀速，

p(W) ~ N[0,Q]：概率分布服从正态分布，期望是0，协方差矩阵为Q

 

如果这个人使用了GPS导航，时刻得到这个人的位置、速度。

那么，第二条模型方程【Z_k = HX_k + V_k】：

Z_1k = X_1k +  V_1,k

Z_2k = X_2k +  V_2,k

p(V) ~ N[0,R]：概率分布服从正态分布，期望是0，协方差矩阵为R

矩阵形式：

 

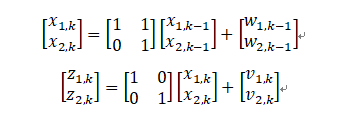
X_k=AX_k-1+W_k-1

Z_k = HX_k + V_k

---

 

DR CAN给出的例子：

 

 

 

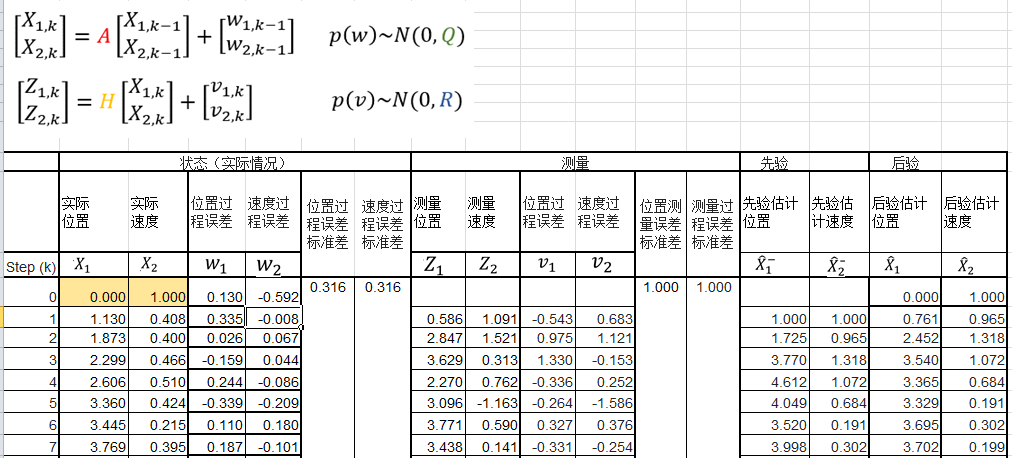
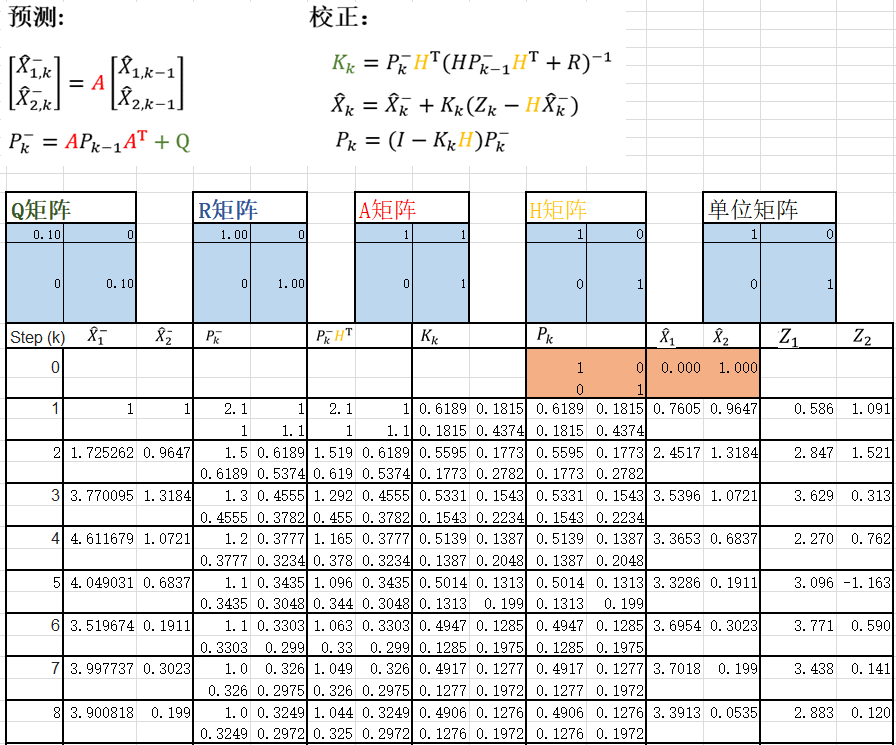
问题一：位置过程误差、速度过程误差是如何得到？DR CAN使用随机数，但是实际上不能用随机数吧？

问题二：Q、R矩阵为什么长这样？

DR CAN视频说，Q、R中，X，Z假设是独立的，所以对角形式。至于其中的数字也是自己编的。

R阵好理解，可以以仪器的标称精度搞得，但是Q应该怎么获得？

 

说明：

1. 位置过程标准差、速度过程标准差，分别是Q对角开根号

2. 位置测量标准差、速度测量标准差，分别是R对角开根号

 

---