卡尔曼滤波（一）
卡尔曼滤波，又名：
最优化、递归、数字处理算法，其实是【观测器】多一点。
主要是对【不确定性】的数据，进行分析和预测。
【不确定性】：
1. 不存在完美的数学模型。（例如：小车的运动轨迹不确定）
2. 系统的扰动不可控，很难建模。
3. 测量传感器存在误差。
例如：测量硬币
测量一个硬币，共测量k次，硬币的直径，很自然就想到k次的均值。
如果将x^ 变换一下，可以发现：
1. 第1~k的均值，可以由第k次的测量值【Zk 】、第1~k-1次的均值【x^ k-1】 ，进行表示。
2. 随着k的次数增多，1 / k * (Zk - x^ k-1) 的作用越来越小，也就是继续测显得意义不大。
令 1 / k = Kk
那么，可以得到如下结论：
1. 利用这种方式【求均值】，不需要知道前面所有的Zk，使用迭代方式求解，不用存储大量数据。
2. 只需要存储：【Zk 】【x^ k-1】 和 k，每次都更新这3个数值即可！
核心公式：
eEST：估计误差。（理解：应该是 【真实值X】-【估计值X^】）
eMEA：测量误差。（理解：应该是由【测量设备标称的测量误差】，或者 f（【测量设备标称的测量误差】），f是误差传播模型）
结论：
1. 当 k - 1 时的【估计误差】>>【测量误差】（远大于），Kk接近1，那么Xk就接近【测量值】，或宁愿相信【测量值（Zk）】，也不相信【估计值（Xk-1）】。
2. 当 k - 1 时的【估计误差】<<【测量误差】（远小于），Kk接近0，那么Xk就接近【估计】，或宁愿相信【估计值（Xk-1）】，也不相信【测量值（Zk）】。
使用卡尔曼滤波进行估计
1. 计算【卡尔曼增益】Kk
2. 计算第k次的估计值（那么起码要第k-1次的初始值才行，k至少为2才能开始计算）
3. 更新【第K次的模型误差（eEST-k）】
实际长度 ：X = 50 （这个一般是未知的）
第0次估计： x^0 = 40 （这个可以使用经验值，或者更粗糙的观测方法得到）
第0次模型误差：eEST-0 = 5（这个可以随便给，一般也是靠经验，又或者叫【估计误差】）
第1次测量值：Z1 = 51
第1次测量误差：eMEA-k = 3 (这个测量误差，每次都是固定的，因为仪器一般是固定的，所以用MEA-k，不用特别区分次数)
上表：
1. 只有Zk 是每次必须要真实测量的观测数据。
2. 其余列都是自动可以计算得到的。
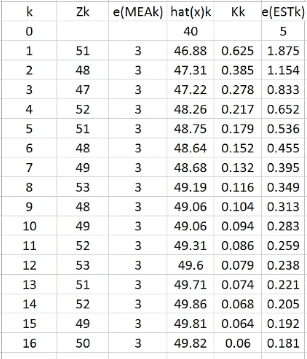
蓝色是Zk，红色是X^k，可以看出，X^k越来越接近50了。
