u检验粗浅理解

假设检验是以小概率事件，在一次实验中是不可能发生为前提(事实上是有可能发生的，但不是这样说的话，就落入一个圈，不能继续玩了)，来否认原假设。

u检验的定义：

已知从正态母体N(u,σ²)中抽得容量为n的子样，求得子样的均值x，而且假设母体的方差σ²  为已知值，那么可利用统计量

u = (x - μ) / (σ / √n)  ~  N(0,1)   

检验母体期望μ是否与某一常数相符进行检验。

（意思是说，我们假设的μ是母体均值，n是样本数，构造了u，u服从正态分布，其均值为0，中误差为1）

---

 

正态分布，可以网上查，就是对某个测量量，均值+误差的概率情况。

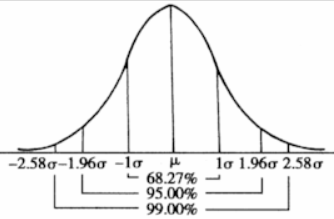（标准正态分布曲线，假设均值u等于0；如果不是标准正态分布曲线，那么u相当于向左向右偏）

例如：对一短距离，测量10000次，得到中误差±σ₁₀₀₀₀ ，已经非常接近1σ 了。

而测了100次，可能得到的中误差在±1σ到±2σ之间。

(所以有一种说法，就是如果做了大量测试，得到某个均值a，中误差σ' (因为我们永远不知道真正的σ，毕竟不能做无限次测试)，假如另外再测一次，得到的值为b ， 如果|b - a| > 2σ ，那么认为b是噪点，毕竟从正态分布来看，大于2σ的值概率已经小于5%了)

---

 那么，u分布到底是怎么回事呢？

(1) 假如已知母体方差σ²  ，意思应该是，已知一个仪器测量的方差 。 (仪器的方差，也是通过大量测试一个量，求方差得出来的，很接近真的σ)

(2) 子样的均值x ，意思应该是，测了多次，例如：1.01，1.01，1.019，1.00，0.999，……，然后求出均值，假如为x，但是≠1

(3) 母体期望μ ， 就是说我们假设的一个值。例如上面，样本均值为x≠1，但是很接近1，那么可以假设μ = 1

（为什么不干脆说，母体期望μ 直接就等于x好了，干嘛多次一举？因为任性…… 如果都这样的话，就不需要搞u检验了，u检验没意义，相当于主观的100%认定μ=x，没必要检验）

---

 u = (x - μ) / (σ / √n)

分母(σ / √n) ， 就是根据误差传播定律，得到x的精度

 所以，u就是：假设值 - 样本均值 : 样本精度 

---

 那么，如何检验？

在假设检验前，还有有一个值，就是对：假设μ = 1的显著水平，一般称为a值进行评估。

如果我们坚信，母体均值μ 就是等于 1 ， “坚信”这个东西，也是有值的；

“坚信”值95%，就是有5%怀疑 “μ 就是等于 1” 是错的。

a的意思是，“怀疑”程度。

如果相信假设的μ就是母体均值 ， 那么a设置小一点，例如：5%（0.05）、1%（0.01）

---

那么，u计算好，有a，就愉快的差表了。

查表，其实就是反算u' ，和u的关系。

看上面正态分布的图：

假设a是5%，那么得到的u' = 0 + 1.96 ， 那么如果  -u' < u < u' ，就说明了这个u在接受域内，假设成立。

---

 

应用：

例子一：测定高温对距离测量的影响

1.  假如在高温度T的时候，测n次距离样本，得到了样本均值x

2.  假如在常温下，大量（比n大得多）测得距离均值为μ 

那么，可以做假设检验：

由于相信μ ，所以设置a = 0.001，表示对μ的怀疑度很低。

如果u超出了接受域，那么认为μ是错的；但是，实际上μ又是对的，因为在条件很好且大量测得的情况下得到的。

所以，有一个结论，就是样本均值x测得很不好，导致拒绝了母体均值为μ的假设。

---

 

例子二：测定粗差

1. 假设测了n(n很大)次距离，得到样本均值x

2. 在和1的条件相同的情况下，测得另外一个距离值，测了m(m远小于n)次，均值为μ

那么可以做假设检验：

由于不太相信μ ，设置a = 0.05，表示对μ的怀疑度高。

如果超出了接受域，那么认为μ是错的，也就是m次的均值μ仍然存在粗差

---

 

更深入：

 u = (x - μ) / (σ / √n)

假设分母是v_i = Bx - l，中，v_i的精度 。 （可以先平差，求出x的精度，然后根据误差传播定律，得到v的精度）

由于v是观测值改正数，其数学期望当然为0，因此μ=0；

如果对一个值，观测了十分多次，那么其观测值改正数当然要为0的了，因此可以将a设小点。

然后做检验。如果在接受域内，那么证明vi是对的；否则vi是错的，有粗差