测绘线性代数(二):以全站仪求坐标精度为例
例子:
已知全站仪先验测角中误差为:e = σhar =σvar ,单位:秒。
测距中误差为:a+b*S 注:b单位: 10-6,S单位:km,也为斜距中误差σsd
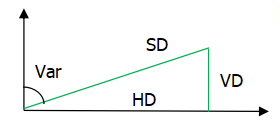
水平距离计算公式:HD = SD * sin(Var),
竖直距离计算公式:VD = SD * cos(Var)
泰勒一阶展开得:(泰勒展开详解参照:https://www.cnblogs.com/pylblog/p/10225053.html)
HD = HD0 + dHD/dSD * (SD-SD0) + dHD/dVar * (Var-Var0) * ρ
VD = VD0 + dVD/dSD * (SD-SD0) + dVD/dVar * (Var-Var0) * ρ
Har = Har
(SD为真正的无误差值,不可知;而SD0 假如仪器精度足够高,和真值差别在0.001位,那么二阶项的位数是10-6 次方,可以忽略二阶乃至高阶项了)
(我不会告诉你,用泰勒一阶展开式代替原式,不考虑高次项的基本条件就是:原值x0 必须要足够接近真值,否则高次项必须考虑)
常数ρ是几个意思呢?
以HD为例子:
dHD/dSD = sin(Var) , Sin(Var) * (SD-SD0) 单位仍然是m
dHD/dVar = SD*Cos(Var) , 单位是m,然而,SD*Cos(Var) (Var-Var0) 单位是 m * ° ,为了使得单位统一,思考一下:
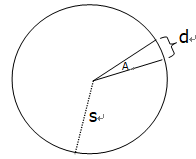
意思是角度误差A,单位:秒,导致在一定距离S下,角度平面方向上造成的距离偏差 :
d / (2 π s) = A / (360*60*60)
d ≈ A * S * 1 / 206265
所以,ρ = 1 / (360*60*60)/ (2 π) ≈ 1 / 206265
由此可得,
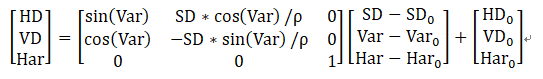
所以:

SD,Var,Har他们观测是相互独立的,属于最底层的独立观测值,所以其协方差可以大胆的写为0了;
同理,我们检验一个坐标的精度,那么:
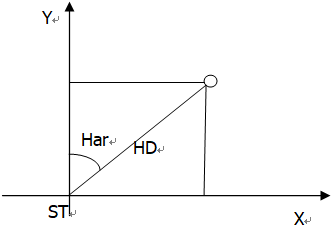
X = Xst + HD * cos(Har)
Y = Yst + HD * sin(Har)
Z = Zst + VD
假如 Xst , Yst ,Zst都无误差的话,泰勒一阶展开,那么:

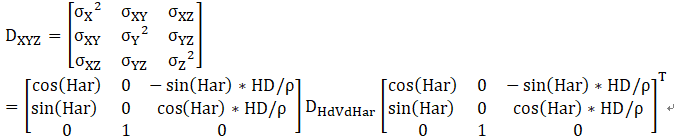
但是, Xst , Yst ,Zst 往往是传导下来的,其实有误差的,那么:

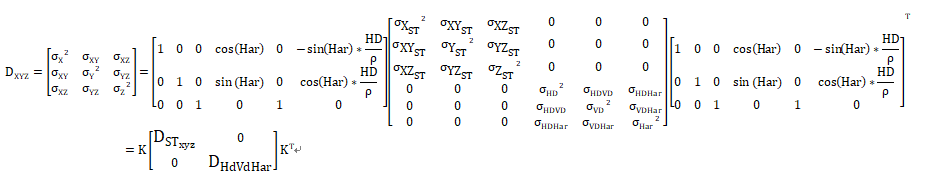


 浙公网安备 33010602011771号
浙公网安备 33010602011771号