测绘线性代数(一):基础
通常来说,线代开始入门,都会从线性方程组开始:
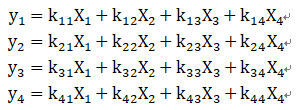
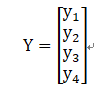


如果我们将y1到y4 整体来看,看作是列向量Y(竖着的向量)的一步分,那么A=[A1,A2,A3,A4],也就是矩阵A,有四个列向量,不难看出
Y = AX = x1A1 + x2A2 + x3A3 + x4A4 (粗体代表向量)
也就是说,列向量Y,是由列向量X的各个分量,对A矩阵中的各个列向量的线性组合。(这仅仅是其中一个几何意义)
由X各行元素,对A列向量线性组合,得到Y列向量
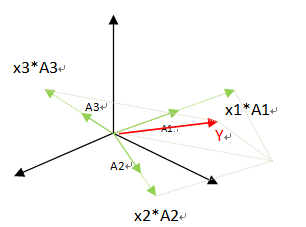
这就解析了,为什么“A列=X行”(前列=后行)。
扩展:
Y =[Y1,Y2],X=[X1,X2],X有多少列,Y就有多少列
假若:
![]()
![]()

将X的每一行,看作一个行向量,那么,行向量Y
Y = k11X1 + k12X2 + k13X3 + k14X4
由A各列元素,对X行向量的线性组合,得到Y行向量
回到解线性方程组的问题
情况一:有唯一解
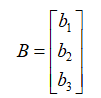
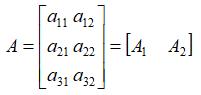

AX=B
换句话说,就是有唯一的X1,X2……,能将A的列向量,线性组合成列向量B
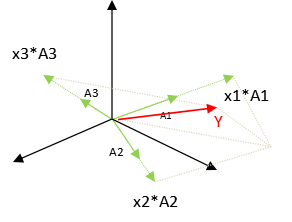 (图1)
(图1)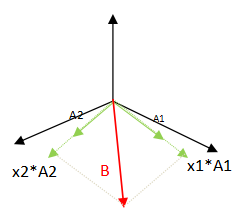 (图2)
(图2)
如果用空间语言来说,B向量,刚好落在就是A的列向量所组成的空间,亦即A的列空间(空间即是立体的三维空间,或者平面的二维空间)。
除此之外,还有一个条件,就是A的列向量要线性无关。等价于:线性无关向量数R=n列(线性相关,就是任一一个向量,能被其他向量线性组合)
情况二:没有唯一解
特点就是,虽然B在A的列空间中,A的列向量线性相关



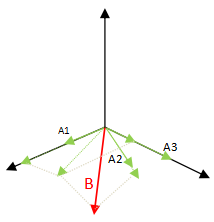
通常,在这种情况下,我们取X向量的长度最小的解为最优解,也就是最小范数解,XTX最小解。
这很重要,讨论某些问题有特殊意义。(如何求最小范数解是个复杂的问题,以后再说)
这种是属于“秩亏”,就是说 R < 行数 && R < 列数 ,在实际求参是比较少见的。
情况三:没有解的第一种情况
特点就是,虽然A的列向量线性无关,但是B也不在A的列空间当中。

这类情况是最常见的。
解就是,将B投影在A的列空间中,再找出X1,X2
情况四:没有解的第二种情况
特点就是,A列向量线性相关,而且B也不在A的列空间中
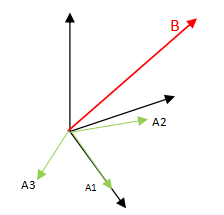
这类情况是最不常见的。
解就是,先将B投影在A的列空间中,再找出X向量的长度最小的解。
先讨论情况三为什么如此普遍:

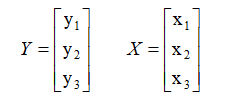

假如要求:y=ax+b
如果:
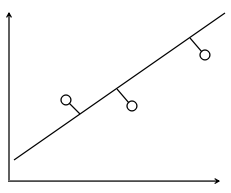
那么,我们求解最优的[a,b],实际上求一条直线,其满足:
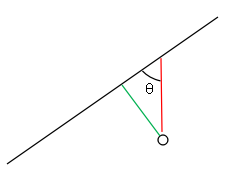
E2=Σ(ax+b-y)²=Σ(y'-y)²=最小
( 可能有时候会困惑,|y'-y|² 应该是红色这段,为什么其最小,会让所有蓝色这段的和最小?原因是:Σ蓝=sinθΣ红,sinθ为一常数。)
Σ(y'-y)² 转化为 :
E2=Σ(ax-b-y)²,F获得极小值,只需要:
dE2/da= 2*Σ*x(ax-b-y)=0等价于Σ*x(ax-b-y)=x1(ax1-b-y1)+x2(ax2-b-y2)+x3(ax3-b-y3)=0(1)
dE2/db= -2*Σ(ax-b-y)=0等价于Σ(ax-b-y)=(ax1-b-y1)+(ax2-b-y2)+(ax3-b-y3)=0(2)
然后变成了解方程组的形式:
aXTX - bXTIc - XTY = 0
a IcT X- b (Ic)T Ic - IcTY= 0
再写成分块矩阵的形式:

再变换一下:

也就是:ATAV=ATY V = (ATA)-1 ATY
我们十分惊讶的发现,最小二乘解参数,只需要在原方程组的矩阵形式AV=Y,左右两边分别左乘AT
先抛开ATA的可逆性问题,以向量的方式,理解一下Y和A的列向量之间的关系。
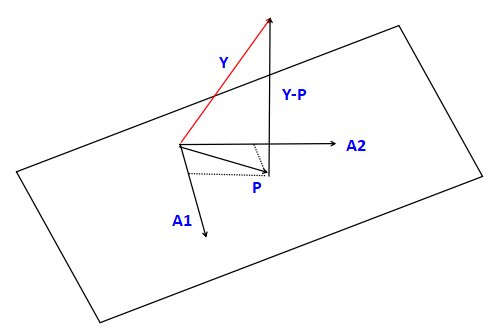
如果A=[A1,A2],有两个列向量,形成列空间。Y不在A的列空间上,P是Y在列空间的投影。
由向量点乘的几何意义,M、N均为列向量,M·N = MTN=|M||N|sinθ,θ是M、N的夹角,几何意义:M在N上的投影长度 X N的长度。如果θ是90度,那么MN垂直,则M·N = MTN=0.
由于P在列空间,总有V=[a,b]T ,使得P=AV;
由于(Y-P)⊥P,所以有 PT(Y - P) = 0
(矩阵相乘法则:(AB)T=BTAT)
等价于:(AV)T(Y-AV)=0
等价于:VTAT(Y-AV)=0
等价于:VTATY -VTATAV = 0
等价于:VT(ATY - ATAV) = 0 , 将V和(ATY - ATAV) 分别看成两向量。
那么,如果我们要找到非零解V,V≠[0,0],那么 ATY - ATAV =0
至此,大功告成。
原来最小二乘解参数,转换为向量模型,可以用矩阵方程来表达,就是左右同时乘以AT ,也就是ATAV=ATY
其几何模型,就是Y在A列空间上的投影等于V对A的列的线性组合
附加一:
AX = P =x1 A1 + x2 A2(A1、A2为A的列向量)
Y-P = Y - AX , 又因为(Y - AX) ⊥ P
PT(Y - AX) = 0
XTAT(Y - AX)=0
XTATAX = XTATY
ATAX = ATY
附加二:
对于AX = b ,最小二乘的要义,就是使得 ||Ax - b|| 向量长度最短(向量长度最短,就是平方和最小,就是最小二乘),那么最直接的就是 b - P的向量最短
附加三:
如果(只有)A各列线性无关,那么ATA是可逆的
证明:
AX = 0 (A各列线性无关,那么Ax = 0 ,只有x全为0,才可能)
ATAX = 0 (这里也成立,既然这里也成立,因为X只能为0 , 因此ATA 各列线性无关,而ATA 又是n * n ,因此满秩,因此可逆 )
XTATAX = 0
(AX)TAX = 0 , YTY =0 , 那么AX = 0,那么X = 0
加权最小二乘法
对于最小二乘的目的:Σ(axi+b-yi)²=Σ(yi'-yi)²=最小
但有时候,我们对每个yi 的重视程度不一样,比如说:第1天(x=1)时,测得的y1是认真测的,或者使用同一个仪器,测了多次求均值的;而第2天,测得的y2 是随便测的;
那么,对于(y1'-y1)² 这个值,我们会十分在意,因为y1 的可信度高;同理,对于对于(y2'-y2)² 这个值,我们不会太在意。(【美】Dan Simon《最优状态估计》P60)
(必须明确的一个东西,就是yi 是测量出来的,而xi 是 a 在格式子的系数,是问题模型自带的,已知的)
在意度,引入一个词,叫“权”。权是相对的。
那么,可能会有E2=1*(y1'-y1)² + 0.5*(y2'-y2)² + ……(1)
使用代数的方式:E2=p1*(y1'-y1)² + p2*(y2'-y2)² + ……(2)
或者:E2=w12*(y1'-y1)² + w22*(y2'-y2)² + ……
又等价于E2=((w1)(y1'-y1))² + ((w2)(y2'-y2))² + ……(3)
又等价于E2=(w1y1'-w1y1))² + (w2y2'-w2y2))² + ……(4)
等等,假如我们有方程组:
w1x1a+w1b=w1y
w2x2a+w2b=w2y
w3x3a+w3b=w3y
用此方程组去求最小二乘V=[a,b]T,其实是符合(4)的!!
也就是:
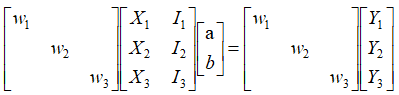
也就是:
WAV=WY
(【美】G.Strang《线性代数及其应用》P159)
假如 V = [ y1'-y1 , y2'-y2 ,…… yn'-yn] ,那么 E2 = VTPV
那么,如果么我们将A' = WA,Y' = WY,那么,最小二乘解,不就是(WA)TWA V =(WA)T WY的解?
等价于:ATWTWAV = ATWTWY(5)
回头看(2)式,不难发现一个事实:

那么,(5)式等价于ATPAV = ATPY (6)
现在,要好好研究矩阵P到底是怎么来的?
问题1:p1,p2,p3……是怎么定的?
问题2:虽然离散式(2)只用到P的对角元素值,但P只能是对角阵吗?
如上面所说,yi 的测量精度越高,那么越在意(yi'-yi)² ,那么pi 越高。
由于p最大为1,最小为0,而且pi和pj 都是相对的。
首先,研究一下测量精度。
精度的概念就是,一批数据的稳定程度。形容稳定程度的办法发,最好就是用均方差了。
(我猜只是有些仪器,为了顾及单位,给出的是中误差)
假如有一台高级一万倍的仪器A,测到某段距离为u。而仪器B,测巨多次n,得到 σ2 = 1 / n * Σ ( x - u)² , 也就是,中误差σ = √ 均方差;
(如果没有仪器A测得的u,那么σ2 = 1 / (n-1) * Σ ( x - avg)² , 原因:https://www.matongxue.com/madocs/607.html)
假如有仪器,其测量一个距离的精度是 σ mm,也就是误差在±σ mm
yi 是对某个距离,测了n次求均值:yi =1 / n * yi1+……+ 1 / n * yin。yii 每个测量精度为σ2 , 根据误差传播定律:
yi 精度 σi 2= σ2 / n
yj 精度 σj 2= σ2 / m
(误差传播定律:y = k1 x1 + k2 x2 + ……+Knxn + C , σy 2 = k1 2 σx12 + k2 2 σx22 +……kn 2 σxn2 ,前提是x1……xn 相互独立,这是一个重要的概念)
(武大测绘《误差理论与测量平差基础》P27)
既然精度越高(σ越小),p越大,而且p要是相对的,那么,不如:
pi = σ2 / σi2 = n
pj = σ2 / σj2 = m
(武大测绘《误差理论与测量平差基础》P43)
可见,权值是可以大于1的。
那如果用矩阵的形式,先试图将P表达出来:
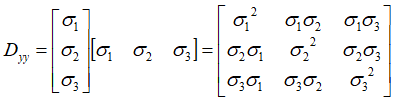
σ12 ,σ22 ,σ32 的影子出来了,但是σiσj 是什么鬼?(后面再说)
假如各个y之间相互独立(再次提及),σiσj = 0,那么:

对Dyy 求逆 ,得到:(后面再讨论求逆)
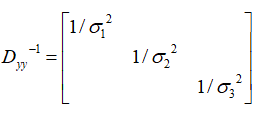
P = σ2 Dyy-1
(又有P=Qyy-1 ,Qyy = 1 / σ2 Dyy)
(武大测绘《误差理论与测量平差基础》P48)
到此,可以急着下一个结论,就是:
P = 仪器精度σ的平方σ2 X 各个观测值的(协)方差阵的逆矩阵
继续思考一下,假如P不是对角阵,那么整个系统的方差(需要注意和均方差的区别)
E2 = VTPV

原本的式子是:
E2=p1*(y1'-y1)² + p2*(y2'-y2)² + ……= p1*v1² + p2*v2² + ……
上面的式子“无故”多了很多相关项。
关于上面围绕P的各种问题,其根源可能要由误差传播定律说起。
有:
y=Cx (1)
那么,很直观的是,如果x采集的数据,有σx 的误差,那么σy = Cσx ,从而有:
σy2 = C2 σX2 (2)
z = Ax + By
z = Ax + B(Cx) = (A+BC)x
如果(2)式子的推论是对的话:
σz2 = (A+BC)2 σx2
σz2 =A2σx2+ 2ABCσx2 + B2C2σx2
σz2 = A2σX2 + B2 σy2 + 2AB√(σy2 /σx2) σx2
σz2 = A2σX2 + B2 σy2 + 2ABσy σx
σxy = σy σx
σz2 = A2σX2 + B2 σy2 + 2ABσxy (3)
那么,在此说明了,对于系统Z的方差,如果x,y是非独立观测(y是关于x的函数),是必须要将其协方差考虑进去的。(是不是开始有点理解上面提及的E2 = VTPV ?)
所以,用矩阵方程表达:
![]()
(武大测绘《误差理论与测量平差基础》P27)
那么,如果y≠Cx,也就是x和y是相互独立观测量(最后一次提及了),y就是y,y=y呢?
σz2 = A2σX2 + B2 σy2 ,这里有一个问题,一元一次我们知道σy2 = C2 σX2 ,但是Z是二元一次,为什么其方差的形式是这样呢?
在几何上,形容两个向量的相关性如何,看其夹角。小于90°正相关,等于90度不相关。

很明显,如果x和y 不相关,那么x长度的增量σX 、y长度的的增量σy 、z长度的增量应该符合勾股定理。
故σz2 = A2σX2 + B2 σy2 (从几何规律可以看出,后边多了那些尾巴是怎么来的了)
那么,要求得这样的结果,显然:
![]()
σxy = 0
一句话总结,如果要求某个量的方差,就不得不往下挖,挖到独立观察量为止,才能获取协方差。
补充:
更详细的解析:https://www.zhihu.com/question/20852004
协方差:
![]()
向量 X(x1 - x',x2 - x' ,.....),Y,那么Σ看作是向量点积,根据点积的几何意义,X⊥Y,那么Sxy 为0;
而X的样本方差:
![]()
Σ自然是看作X(x1 - x',x2 - x' ,.....) 的长度平方了。




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· AI与.NET技术实操系列:基于图像分类模型对图像进行分类
· go语言实现终端里的倒计时
· 如何编写易于单元测试的代码
· 10年+ .NET Coder 心语,封装的思维:从隐藏、稳定开始理解其本质意义
· .NET Core 中如何实现缓存的预热?
· 分享一个免费、快速、无限量使用的满血 DeepSeek R1 模型,支持深度思考和联网搜索!
· 基于 Docker 搭建 FRP 内网穿透开源项目(很简单哒)
· ollama系列01:轻松3步本地部署deepseek,普通电脑可用
· 25岁的心里话
· 按钮权限的设计及实现