使用“反向传播”迭代法求解y=√10

X=√10，求X，也就是求Y=10 =X² , X是多少。

*重要的思想是，如何转化为可迭代求解的算法问题。

*解数学问题，第一时间画图，求导，“直线化”。

Y = X²

假如已知Y = 10 ，要求解X；

1. 令X=3，解得 y = 9 ;

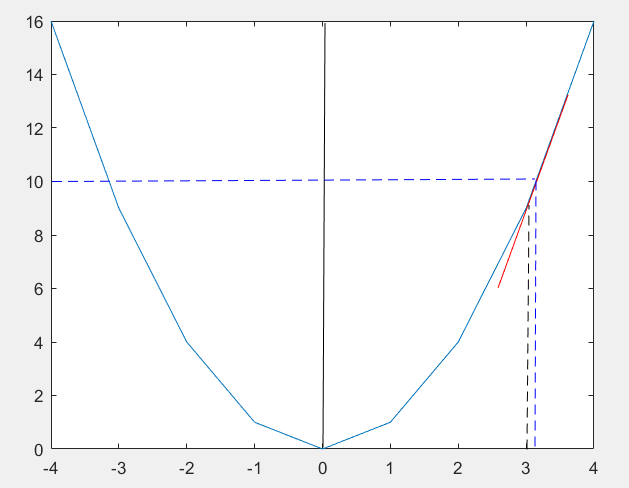
那么，自然是希望，在X=3处，加上一个△X，得到

Y = y + k * △X ≈ 10；

已知，在X=3处，k = dy / dx = 2*X = 6，所以 △X = [(Y - y) / k]  = △Y / k 

我们也可以使用等式：△Y / △X = dY / dX  等价于  1 / △X  =  6  ，△X = 1 / 6 ；

 *在微分中，当△X很小时，△Y / △X = dY / dX；当X取得很接近真值时，认为△X很小。（下面讨论当△X比较大，也就是X取得不接近真值的情况）；

2. 令X = X + △X = 3 + 1 / 6 = 3.16666666 ；y = 10.19444444；dY/dX =2X = 6.3333333；

△Y = 10 - 10.19444444 = -0.1944444444比之前更小了，解得△X = -0.03070；

3. 令X = X + △X = 3.13596666666；y = 9.834287；dY/dX = 2X = 6.27193333

△Y = 10 - 9.8342869344 = -0.1657130

.....

直到△Y满足精度为止；

 

由△Y（损失），求出△X（改正数）

再由X =X + △X，回代，求出Y'

△Y=Y-Y'（损失），求出△X（改正数）

再由X =X + △X，回代，求出Y''

。。。。。。

---

如果预测值X=1，和结果相差比较大，再看看；

 

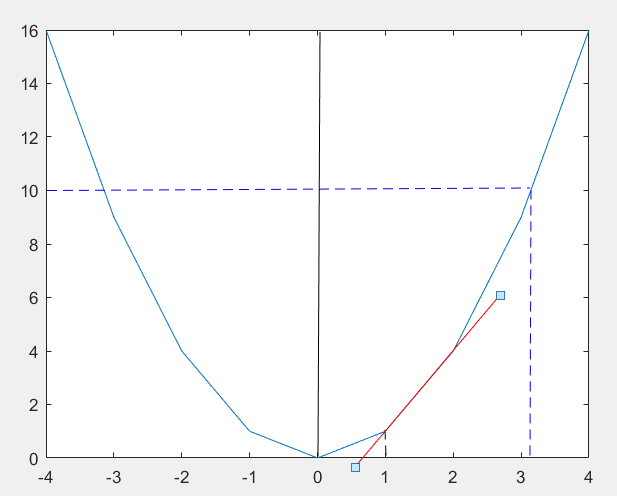
1. 令X=1，解得 y = 1 ，dY/dX = 2X  = 2 ;

△Y = 10 - 1 = 9 ，△X = 9 / 2 = 4.5；

2. X = X + △X = 5.5 ， 解得 y = 30.25， dY/dX = 2X  = 11

△Y = 10 - 30.25 = -20.25， △X = -20.25 / 11 =  -1.84091 

3. X = X + △X = 3.65909， 解得 y = 13.38894， dY/ dX = 2X  = 7.31818

△Y = 10 - 13.38894  = -3.38894，△X = -3.38894 / 7.31818 =  -0.4630851

4.  X = X + △X =  3.196005，解得 y = 10.21445，dY/ dX = 2X  = 6.39201

△Y = 10 - 10.21445 = -0.21445 ，△X = -0.21445 /  6.39201 = -0.0335497

5. X = X + △X =  3.1624553，解得 y = 10.001124，dY/ dX = 2X  = 6.3249106

△Y = 10 - 10.21445 = -0.001124

....

X的预估值为1，离真值比较远，所以第2步出现“矫枉过正”的现象，但随即又修复了，因为每处在新的位置，都更新了X 和dY/ dX。