极小化极大估计
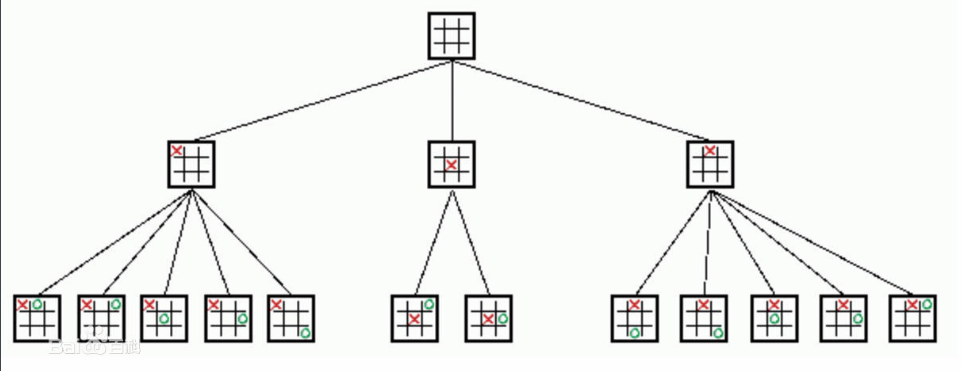
以上内容来源于百度百科,作为引子。
假如棋局进行到某一步,只需要预测到,下一层,哪一个方向更合适;
那么,如果直到最后的各个“局势”值,那么就可以逆回去,“综合”求得,当前应该选哪一个方向。
如何用算法,表现这个过程??
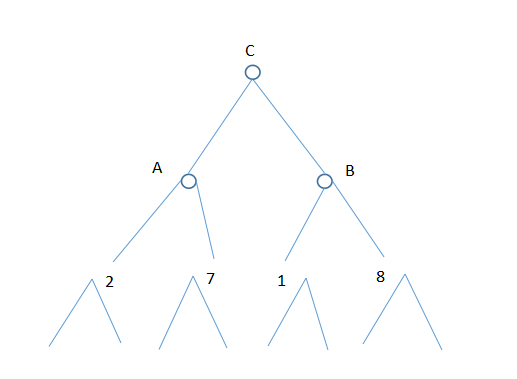
如果棋局进行到2层A处,轮到极小者玩家下棋,那么极小值玩家,肯定会偏向2;
如果棋局进行到2层B处,轮到极小者玩家下棋,那么极小值玩家,肯定会偏向1;
那么在1层C处,轮到极大值玩家下棋,他只能选择往A,因为选择往B,轮到极小者玩家下棋时,必定选1;
所以如果极大者玩家,他最优的选择是A;
alpha-beta 剪枝
就是优化算法,不对deepth处所有的节点进行遍历计算
function alphabeta(node, depth, α, β, Player) if depth = 0 or node is a terminal node return the heuristic value of node if Player = MaxPlayer // 极大节点 for each child of node // 极小节点 α := max(α, alphabeta(child, depth-1, α, β, not(Player) )) if β ≤ α // 该极大节点的值>=α>=β,该极大节点后面的搜索到的值肯定会大于β,因此不会被其上层的极小节点所选用了。对于根节点,β为正无穷 break (* Beta cut-off *) return α else // 极小节点 for each child of node // 极大节点 β := min(β, alphabeta(child, depth-1, α, β, not(Player) )) // 极小节点 if β ≤ α // 该极大节点的值<=β<=α,该极小节点后面的搜索到的值肯定会小于α,因此不会被其上层的极大节点所选用了。对于根节点,α为负无穷 break (* Alpha cut-off *) return β (* Initial call *) alphabeta(origin, depth, -infinity, +infinity, MaxPlayer)
*每一个node,就是一个局势,一种下一步要落棋子的局势。虽然可以对小于deepth的Node,求得s,但是显然没看到最后,暂时s是极大或极小,不代表后边不能走向相反的结果;
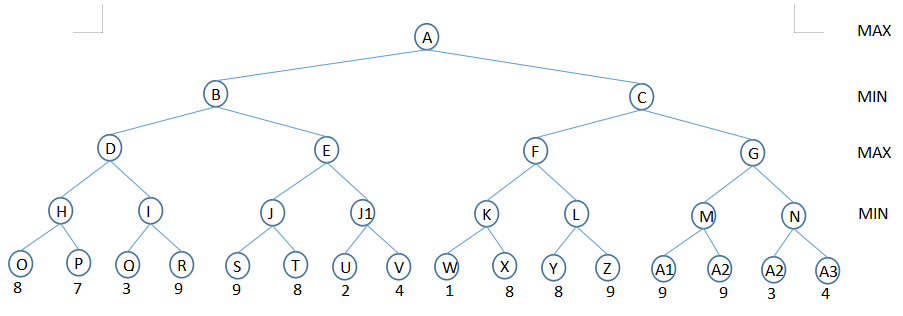
*算法本身是返回node的值,所以,对于A点,需要获得B,C的值,然后选择最大的值,作为“下一步棋”;
直接以A的Node调用,看看如何“裁枝”,提高效率
参考: https://blog.csdn.net/joshualiunsw/article/details/52131507
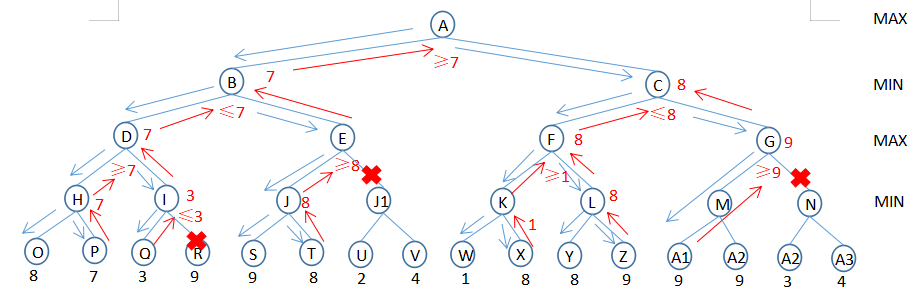
当遍历到I节点的时候,刚遍历完Q,得到3;
按照算法,I节点获得β=3,那他的下一个分支,目标是找≤3,找不到就用β=3做为I处的值;
同时,知道对手,想要使得a≥7;因为β=3<a足够阻止对手,所以不用看R了;
当遍历到E节点的时候,刚遍历完J,得到8;
按照算法,J节点获得a=8,那他的下一个分支,目标是找≥8,找不到就用a=8做为J处的值;
同时,知道对手,想要使得β≤7;因为a=8>β足够阻止对手,所以不用看J1了;
一句话,知道上一步对手想要什么,自己先遍历一侧得到的值,足以阻止对手的话,另一侧就不用遍历了;





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· AI与.NET技术实操系列:基于图像分类模型对图像进行分类
· go语言实现终端里的倒计时
· 如何编写易于单元测试的代码
· 10年+ .NET Coder 心语,封装的思维:从隐藏、稳定开始理解其本质意义
· .NET Core 中如何实现缓存的预热?
· 分享一个免费、快速、无限量使用的满血 DeepSeek R1 模型,支持深度思考和联网搜索!
· 基于 Docker 搭建 FRP 内网穿透开源项目(很简单哒)
· ollama系列01:轻松3步本地部署deepseek,普通电脑可用
· 25岁的心里话
· 按钮权限的设计及实现