最佳路径搜索算法2

问题：假如有人提出，最佳的路径是SADG，那么，将如何验证？

答：遍历其他路径，看看是否存在，比SADG更短的路径。

问题：其他路径是否需要"扩展"到最后？

答：不需要。

 

在检验其他路径的时候，如果累积路程大于SADG，即11，就不需要再扩展下去了。

---

 

根据上一节：https://www.cnblogs.com/pylblog/p/10287740.html

广度优先查找路径的基础上，添加：在扩展到目的点G的时候，继续扩展其他路径，除非这条路径长度大于上一条到达G的路径。

伪代码：

暂时最佳路径 P

while(T.Count>0)

{

　　　　if ( 能T[0]的下一个节点 的数目n > 0  ) {

　　　　　　　　　　 foreach n 个节点　　{

　　　　　　　　　　　　if ( 节点为G) {　

 　　　　　　　　　　　　　　temp = T[0] + G的路径；

　　　　　　　　　　　　　 　if( temp的路径长度 < P的路径长度 ){

　　　　　　　　　　　　　　　　P = temp;

　　　　　　　　　　　　　　 }

　　　　　　　　　　　　}

　　　　　　　　　　　　else　{

　　　　　　　　　　　　　　if(节点没有被扩展过 && T[0]+节点的扩展路径长度 < P的路径长度){

　　　　　　　　　　　　　　　　“  T[0]+节点的扩展路径 ” 插入到T的后面；

　　　　　　　　　　　　　　}

　　　　　　　　　　　　}

　　　　　　　　　　} 

　　　　} 

　　　　移除T的第0个元素

}

---

 

上面的算法，面临一个问题，就是效率不高。

假设：起点和终点，如下

 

假如有很多路径，是向“左”，如果采用上述算法，会导致：

不能较快速查找一条可行线路，从而导致，有些可以中途放弃扩展的线路继续扩展。

因此，可以在上面的基础上，使用启发信息。

因此，改进的部分，是更快速的找到一条可行线路。

距离下限法：

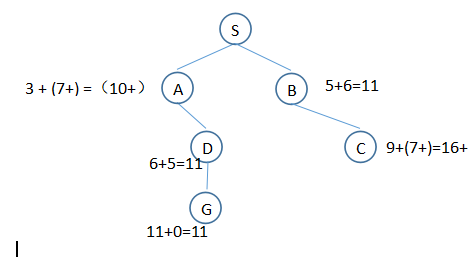
主要区别：距离下限 =  算出到达节点的长度 + 最后一个节点到目标点的距离估计，并且将最低的放到列表的最前一个位置

1. S

2. (S,A) (S,B)

3. (S,A,D) (S,B)

4. (S,A,D,G)(S,B) 接下去查看有没更短路径

5. (S,B,C)

 

暂时最佳路径 P

while(T.Count>0)

{

　　　　if ( 能T[0]的下一个节点 的数目n > 0  ) {

　　　　　　　　　　 foreach n 个节点　　{

　　　　　　　　　　　　if ( 节点为G) {　

 　　　　　　　　　　　　　　temp = T[0] + G的路径；

　　　　　　　　　　　　　 　if( temp的路径长度 < P的路径长度 ){

　　　　　　　　　　　　　　　　P = temp;

　　　　　　　　　　　　　　 }

　　　　　　　　　　　　}

　　　　　　　　　　　　else　{

　　　　　　　　　　　　　　if(节点没有被扩展过 && T[0]+节点的扩展路径长度 < P的路径长度){

　　　　　　　　　　　　　　　　“  T[0]+节点的扩展路径 ” 插入到T的后面；

　　　　　　　　　　　　　　}

　　　　　　　　　　　　}

　　　　　　　　　　} 

　　　　} 

　　　　移除T的第0个元素；

　　　　将T中，距离下限最短的路径，放到0序号处；

}

 

---

 

 

上面的算法，有一个问题，就是：

如果实际距离，和估算距离，不是使用同一个数学模型，或者维度，那么会导致错误。

例如：

红色字体，代表点到G的距离估计值，那么，按上述办法：

1. (S)

2. (S,B) (S,A)   1+0=0,1+100=1

3. (S,B,C)(S,A) 1+10+0=11,1+100=1

4. (S,B,C,G)

但是，实际上，SBCG的路程，是1+10+100=111，而SACG是1+1+100=102

这就好比，拿一张只有平面二维坐标的地图，去估计山脚到山顶的最短路径，而不考虑高差一样