最佳路径搜索算法1
算法，就是(结合各种数学知识)解决问题的有限步骤，可以表现为程序、流程图。
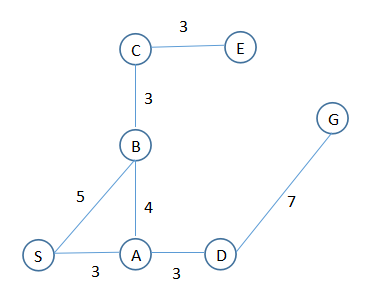
假设要寻找一条路径，从起点S，终点G。
有几个关键原则：
1. 路径的下一个节点，不能和以往节点相同，否则会造成死循环。
2. 所有“待选”，“待算”路径，放在一个列表中；
OK，现在可以假设，有基础数据，各个点的坐标：
struct Point {
char ID；
double x;
double y;
}
各个可走路径的长度
struct distance
{
char Id1;
char id2;
double lenght;
}
那么，我们想要的结果，是：
struct Path {
List<int> Ids; //一个有序的节点集合
}
british museum算法
这个算法，说白了就是构造一颗树，没什么目的的构造，造到死胡同为止，最后看看那条包含S和G
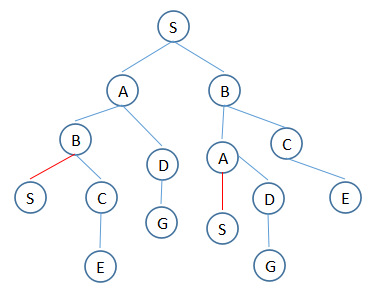
要实现这个算法，需要两个列表，一个存放所有走到死胡同的路径R，一个存放还没走到死胡同的路径T。
被划去的路径，例如：在上一步演变到下一步中划去的。
算法开始：
1. T：(S) R：空
2. T：(S,A)，(S,B) R：空
3. T：(S,A,B)，(S,A,D)，(S,B) R：空
4. T：(S,A,B,C)，(S,A,D)，(S,B) R：空
5. T：(S,A,B,C,E)，(S,A,D)，(S,B) R：空
6. T：(S,A,D,G)，(S,B) R：(S,A,B,C,E)
7. T：(S,B,A)，(S,B,C) R：(S,A,B,C,E)，(S,A,D,G)
8. T：(S,B,A,D)，(S,B,C) R：(S,A,B,C,E)，(S,A,D,G)
9. T：(S,B,A,D,G)，(S,B,C) R：(S,A,B,C,E)，(S,A,D,G)
10. T：(S,B,C,E) R：(S,A,B,C,E)，(S,A,D,G)，(S,B,A,D,G)
11. T：空 R：(S,A,B,C,E)，(S,A,D,G)，(S,B,A,D,G)，(S,B,C,E)
12. 看看R中那条路径含有S和G，S到G的距离那条最短即可。
伪代码：
while(T.Count > 0)
{
if ( T[0]的最后一个节点不是G && 能T[0]的下一个节点 的数目n > 0 )
复制n个T[0]，然后分别往后边添加可添加的节点;
移除T的第0个元素；
将新的n个队列插入到T的前面；
else
将T的第0个元素放进R；
移除T的第0个元素；
}
deepth first（深度优先）算法
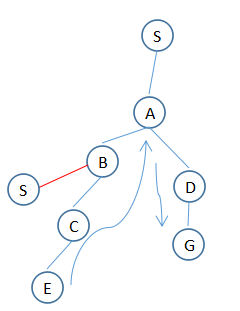
和british museum算法不同的地方是：1. 不需要结果列表；2. 发现目标马上停下来；3. 有回溯
缺点：不能总是发现最优路径
1. T：(S)
2. T：(S,A)，(S,B)
3. T：(S,A,B)，(S,A,D)，(S,B)
4. T：(S,A,B,C)，(S,A,D)，(S,B)
5. T：(S,A,B,C,E)，(S,A,D)，(S,B)
6. T：(S,A,D,G)，(S,B)
伪代码：
while(T.Count>0)
{
if ( 能T[0]的下一个节点 的数目n > 0 )
if （能加在T[0]后的节点有G）
返回T[0] + G的路径
else
复制n个T[0]，然后分别往后边添加可添加的节点;
移除T的第0个元素
将新的n个队列插入到T的前面（这个是算法最要特点）
else
移除T的第0个元素
}
breadth first(广度优先)算法
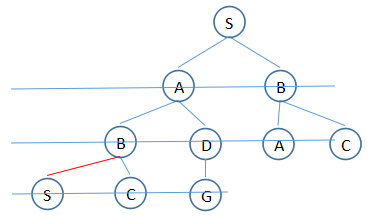
和british museum算法不同的地方是：1. 实现上将扩展后的路径，放到列表后边；2. 没回溯
比深度优先的优点是，更早发现路径浅的路线，虽然本例子是同一个，但难保“右”边出现G比较快。
缺点：较“浅”的不一定是路径最短的。
1. T：(S)
2. T：(S,A)，(S,B)
3. T：(S,B)，(S,A,B)，(S,A,D)
4. T：(S,A,B)，(S,A,D)，(S,B,A)， (S,B,C)
5. T：(S,A,D)，(S,B,A)， (S,B,C)，(S,A,B,C)
6. T：(S,B,A)， (S,B,C)，(S,A,B,C)，(S,A,D,G)
breadth first(广度优先)算法的优化
以上，无论哪个算法，都会对同一节点考虑多次，例如：
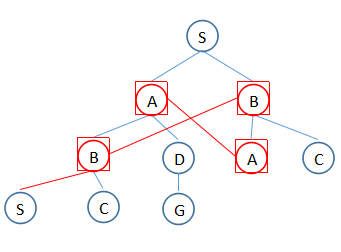
那么，优化的地方是，考虑过的节点不再考虑，变为：
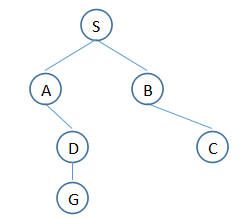
1. T：(S)
2. T：(S,A)，(S,B)
3. T：(S,B)，(S,A,D)
4. T：(S,A,D)， (S,B,C)
5. T：(S,B,C)，(S,A,D,G)
在实现上，对比广度算法，只需要在添加到列表后边前，去除部分不再考虑的节点。
hill climing算法：在深度优先的基础上改进
有不断扩展节点，回溯，使用启发信息的特点
特点：在深度优先的基础上，只考虑离目标直线距离最近的节点。
区别： 在将新的路线插入队列前，先根据离目标的距离，按升序排列。
缺点：这种是一种比较“短视”的算法。
优点：如果路网太复杂的话，效果可能更好
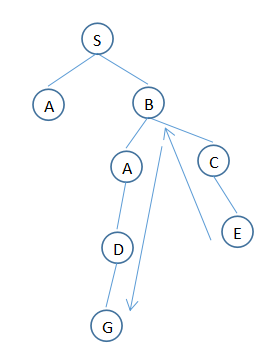
1. T：(S)
2. T：(S,B)，(S,A) （这里发生了排序）
3. T：(S,B,C)，(S,B,A)，(S,A) （这里发生了排序）
4. T：(S,B,C,E)，(S,B,A)，(S,A)
5. T：(S,B,A,D)，(S,A)
6. T：(S,B,A,D,G)，(S,A)
束搜索：广度优先的改良，使用“知情启发信息”
区别：1. 在广度优先中，限制每一层中考虑的路径数量w；2. 节点重复的不考虑；3. 将距离教小的值放到队列前面
关键：设置好w值
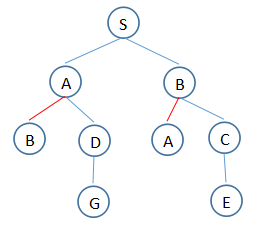
1. T：(S)
2. T：(S,B) ，(S,A) //B点比A点近
3. T：(S,A)，(S,B,C)
4. T：(S,B,C)，(S,A,D)
5. T：(S,A,D) ，(S,B,C,E)
6. T：(S,A,D,G)
伪代码：
while(T.Count>0)
{
if ( 能T[0]的下一个节点 的数目n > 0 )
if （能加在T[0]后的节点有G）
返回T[0] + G的路径；
else
移除n个节点中，在路径已经出现过节点
复制 ≤ n个T[0]，然后分别往后边添加可添加的节点;
移除T的第0个元素；
对 ≤ n个T[0]延伸路径，根据最后一个节点对G点的距离，按升序排列，并取前w个T[0]的延伸路径；（这个是算法主要特点）
将新w个T[0]的延伸路径插入到T的后面（这个是算法主要特点）
else
移除T的第0个元素
}
| 搜索办法 | 回溯 | 节点扩展 | 使用启发式信息 | 扩展路径插入方式 |
| british museum | false | false | false | |
| 深度优先(deepth first) | true | true | false | 前 |
| 广度优先(breath first) | false | true | false | 后 |
| 爬山算法(hill climing) | true | true | true | 前 |
| 束搜素 | false | false | true | 后 |
*节点扩展，在实现上，将新的扩展路径加入到队列的前面；思想上，是否对新的扩展路径“一路走到黑”
*回溯，在实现上，将新的扩展路径加入到队列的前面；新的路径走到死胡同后，及时丢弃；
*启发式信息，是否使用坐标值来优化
