球的面积和体积公式推导
前言
- 高中必修二的立体几何单元讲球的面积的时候就是直接抛出一个公式,没有丝毫证明,就觉得挺不严谨的,感觉还是要证明一下。
证明
前置知识🧀:
没啥别的,会微积分就行。好吧不会的可以看看这里。
……
\(And...\) 首先我们证明一下如何在球的表面积和体积之间建立联系。
显然,可以用微分的思想,我们把球的表面分成许多个小方格,然后连接球心和每个小方格的顶点,将整个球分成很多个“锥体”,求和即可。
\[V=\sum\frac{1}{3}s_iR=\frac{1}{3}R\sum s_i=\frac{1}{3}SR \]当方格分的越多,计算结果就会越接近真实值。
这样我们就建立起了球的面积和体积之间的联系,可以知一求二。
正式证明:
-
既然可以通过体积去求表面积,那么我们不妨就先求一下体积。
-
显然运用微分的思想,我们可以假设将球切成了很多很多片,每一片都可以近似于一个高无限趋近于 \(0\) 的圆柱。
-
先考虑半球,那么显然我们就可以通过积分得到:
\[\begin{aligned} V'&=\int_0^r\pi(r^2-x^2)dx\\ &=\pi r^3-\pi \int_0^rx^2dx\\ &=\pi r^3-\frac{1}{3}\pi r^3\\ &=\frac{2}{3}\pi r^3\\\\ \therefore V&=2V'=\frac{4}{3}\pi r^3 \end{aligned} \]至此我们就得到了球的体积公式,然后我们就可以通过这个公式得到球的面积公式。
后话
-
其实也可以用微分直接求球的表面积,先给出一个定理:球的表面积等于其外接棱柱的侧面积。
-
我们仍然可以将球的表面分成无穷多个小方格,然后假设球的某一条过球心的轴会向外发光。这时每个小方格都会在圆柱上留下投影,通过一些简单的平面几何的证明即可得到其长的比和宽的比互为倒数,所以其面积是一样的。
-
放个图可能会好理解一些:
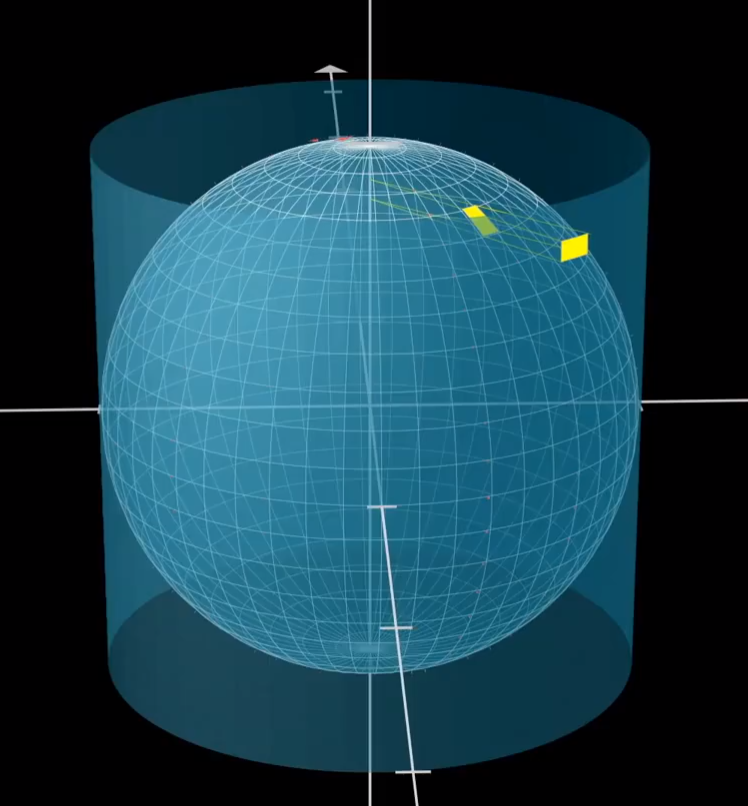
靡不有初,鲜克有终


 浙公网安备 33010602011771号
浙公网安备 33010602011771号