Pytorch

1. SGD
- 1.1 weight_decay
- 1.2 momentum
2.EMA指数移动平均
3.乘法
3、torch.gather(input, dim, index, *, sparse_grad=False, out=None)

1. SGD

1.1 weight_decay

既不是为了提高精确度也不是提高收敛速度，目的是防止过拟合. 损失函数中，weight decay是放在正则项（regularization）前面的一个系数，正则项一般指示模型的复杂度，所以weight decay的作用是调节模型复杂度对损失函数的影响，若weight decay很大，则复杂的模型损失函数的值也就大

import torch
import numpy as np

np.random.seed(123)
np.set_printoptions(8, suppress=True)

x_numpy = np.random.random((3, 4)).astype(np.double)
w_numpy = np.random.random((4, 5)).astype(np.double)
x_torch = torch.tensor(x_numpy, requires_grad=True)
w_torch = torch.tensor(w_numpy, requires_grad=True)
print('Original weights', w_torch)
lr = 0.1
sgd = torch.optim.SGD([w_torch], lr=lr, weight_decay=0)
y_torch = torch.matmul(x_torch, w_torch)
loss = y_torch.sum()
sgd.zero_grad()
loss.backward()
sgd.step()
w_grad = w_torch.grad.data.numpy()
print('0 weight decay', w_torch)

#######################################################
w_torch = torch.tensor(w_numpy, requires_grad=True)
print('Reset Original weights', w_torch)
sgd = torch.optim.SGD([w_torch], lr=lr, weight_decay=1)
y_torch = torch.matmul(x_torch, w_torch)
loss = y_torch.sum()
sgd.zero_grad()
loss.backward()
sgd.step()
w_grad = w_torch.grad.data.numpy()
print('1 weight decay', w_torch)

1.2 momentum

梯度下降法中一种常用的加速技术，一般的SGD，其表达式为,x沿负梯度方向下降。而带momentum项的SGD则写生如下形式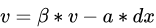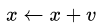：其中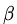即momentum系数，通俗的理解上面式子就是，如果上一次的momentum（即）与这一次的负梯度方向是相同的，那这次下降的幅度就会加大，所以这样做能够到加速收敛的过程

2.EMA指数移动平均

对模型的参数做平均，以求提高测试指标并增加模型鲁棒

深度学习的优化过程中，θt 是t时刻的模型权重weights，vt是t时刻的影子权重，在梯度下降的过程中，会一直维护着这个影子权重，但是这个影子权重并不会参与训练。基本的假设是，模型权重在最后的n步内，会在实际的最优点处抖动，所以我们取最后n步的平均，能使得模型更加的鲁棒

class ModelEMA:
    """ Updated Exponential Moving Average (EMA) from https://github.com/rwightman/pytorch-image-models
    Keeps a moving average of everything in the model state_dict (parameters and buffers)
    For EMA details see https://www.tensorflow.org/api_docs/python/tf/train/ExponentialMovingAverage
    """
    def __init__(self, model, decay=0.9999, tau=2000, updates=0):
        # Create EMA
        self.ema = deepcopy(de_parallel(model)).eval()  # FP32 EMA
        # if next(model.parameters()).device.type != 'cpu':
        #     self.ema.half()  # FP16 EMA
        self.updates = updates  # number of EMA updates
        self.decay = lambda x: decay * (1 - math.exp(-x / tau))  # decay exponential ramp (to help early epochs)
        for p in self.ema.parameters():
            p.requires_grad_(False)
    def update(self, model):
        # Update EMA parameters
        with torch.no_grad():
            self.updates += 1
            d = self.decay(self.updates)

            msd = de_parallel(model).state_dict()  # model state_dict
            for k, v in self.ema.state_dict().items():
                if v.dtype.is_floating_point:
                    v *= d
                    v += (1 - d) * msd[k].detach()

    def update_attr(self, model, include=(), exclude=('process_group', 'reducer')):
        # Update EMA attributes
        copy_attr(self.ema, model, include, exclude)

3.乘法

*按位置，存在广播机制

import torch
vec = torch.arange(4)
mtx = torch.arange(12).reshape(4,3)
print(vec*vec)
print(mtx*mtx)
>>
tensor([0, 1, 4, 9])
tensor([[  0,   1,   4],
        [  9,  16,  25],
        [ 36,  49,  64],
        [ 81, 100, 121]])

torch.mul数乘

import torch
vec = torch.arange(4)
mtx = torch.arange(12).reshape(3,4)
print(torch.mul(vec,2))
print(torch.mul(mtx,2))
>>
tensor([0, 2, 4, 6])
tensor([[ 0,  2,  4,  6],
        [ 8, 10, 12, 14],
        [16, 18, 20, 22]])

torch.mv矩阵向量相乘,对矩阵mat和向量vec进行相乘。如果mat 是一个n×m张量，vec 是一个m元 1维张量，将会输出一个n 元 1维张量。必须前边是矩阵后边是向量，维度要符合矩阵乘法。出来的是一维张量

import torch
vec = torch.arange(4)
mtx = torch.arange(12).reshape(3,4)
print(torch.mv(mtx,vec))
>>
tensor([14, 38, 62])

torch.mm矩阵乘法,对矩阵mat1和mat2进行相乘。如果mat1 是一个n×m张量，mat2 是一个 m×p张量，将会输出一个 n×p张量out

import torch
mtx = torch.arange(12)
m1 = mtx.reshape(3,4)
m2 = mtx.reshape(4,3)
print(torch.mm(m1, m2))
>>
tensor([[ 42,  48,  54],
        [114, 136, 158],
        [186, 224, 262]])

torch.dot点乘积,计算两个张量的点乘积（内积），两个张量都为一维向量

import torch
vec = torch.arange(4)
print(torch.dot(vec, vec))
>>
tensor(14)

@,严格按照第一个参数的列数要等于第二个参数的行数
使用一个@就可以替代上边的那三个函数。
对一维张量执行@操作就是dot
对一维和二维张量执行操作就是mv
对二维张量执行@操作就是mm

import torch
vec = torch.arange(4)
mtx = torch.arange(12)
m1 = mtx.reshape(4,3)
m2 = mtx.reshape(3,4)
print(vec @ vec)
print(vec @ m1)
print(m2 @ vec)
print(m1 @ m2)
>>
tensor(14)
tensor([42, 48, 54])
tensor([14, 38, 62])
tensor([[ 20,  23,  26,  29],
        [ 56,  68,  80,  92],
        [ 92, 113, 134, 155],
        [128, 158, 188, 218]])

torch.matmul,跟@看起来差不多，也是可以:
对一维张量执行操作就是dot
对一维和二维张量执行操作就是mv
对二维张量执行操作就是mm

vec = torch.arange(3)
mtx = torch.arange(12).reshape(3,4)
print(torch.matmul(vec,mtx))
print(torch.matmul(vec,vec))
print(torch.matmul(mtx.T,mtx))
print(torch.matmul(mtx.T,vec))
>>
tensor([20, 23, 26, 29])
tensor(5)
tensor([[ 80,  92, 104, 116],
        [ 92, 107, 122, 137],
        [104, 122, 140, 158],
        [116, 137, 158, 179]])
tensor([20, 23, 26, 29])

3、torch.gather(input, dim, index, *, sparse_grad=False, out=None)

https://pytorch.org/docs/stable/generated/torch.gather.html?highlight=gather#torch.gather
input张量tensor按照索引取值，dim为变化索引的维度取值，其他维度按照0-N维度大小先后取值即可，index为变化索引的具体指

import torch
tensor_0 = torch.arange(3, 12).view(3, 3)
print(tensor_0)
>>tensor([[ 3,  4,  5],
        [ 6,  7,  8],
        [ 9, 10, 11]])

index = torch.tensor([[2, 1, 0]])
tensor_1 = tensor_0.gather(0, index)        # 行按照index 先后取值，其他维度0-2顺序取值，因此，取值坐标就是[(2,0), (1,1), (0,2)]
print(tensor_1)
>>tensor([[9, 7, 5]])

posted @ 2022-04-21 22:27 哈哈哈喽喽喽阅读(118) 评论(0) 编辑收藏举报

刷新页面返回顶部

哈哈哈喽喽喽