boxcox1p

大多数机器学习模型对非正态分布的数据的效果不佳，因此，我们对数据进行变换boxcox1p
https://zhuanlan.zhihu.com/p/53288624

搭建模型，特别是线性模型是希望数据符合正态分布的，但现实中的数据并不符合。

今天讲讨论其中的一种情况。

长跑比赛中，跑得最快的几个人之间相差的时间很短。而最慢的跑步者之间，跑步完成时间差异将非常大。这种现象被称为“异方差性”。在这个例子中，变异量取决于平均值(完成时间短的差异小，完成时间长的差异大)。

画出分布图可以看到，这显然不是正态分布的钟形曲线。为了解决这个问题，就需要转化数据使之符合正态分布。但开始之前，我们需要衡量上图的这种“偏离”程度。于是我们引入“偏度”这个概念。

偏度skewness，表征分布函数曲线相对于平均值的不对称程度。直观看来就是分布函数曲线尾部的相对长度。
正态分布的偏度为0，则：两侧尾部长度对称；
偏度为负，即负偏离（左偏离），则：数据位于平均值左边的比右边的少，直观表现为左边的尾部相对于右边的尾部要长。
偏度为正，即正偏离（右偏态），则：数据位于平均值右边的比左边的少，直观表现为右边的尾部相对于左边的尾部要长。
右偏时：平均数>中位数>众数，左偏时：众数>中位数>平均数。正态分布三者相等。

代码：

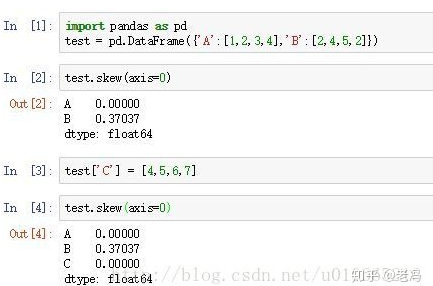
Box-Cox转换
解决这个问题的一个方法是使用Box-Cox转换将数据转换为正态。

这里λ是一个待定变换参数。对不同的λ，所做的变换自然就不同。它包括了对数变换（λ=0），平方根变换（λ=1/2）和倒数变换（λ＝-１）等常用变换。那么怎么去确定呢，这里使用的方法是假设经过转换后的因变量就是服从正态分布的，然后画出关于[公式]的似然函数，似然函数值最大的时候[公式]的取值就是这里的值。##因此会结合boxcox_normmax进行使用，比如 features[column] = boxcox1p(features[column], boxcox_normmax(features[column] + 1))

如果对图二分布进行对数变换，较小数据之间的差异将会变大(因为对数函数的斜率很小)，而较大数据之间的差异将减少(因为该分布中较大数据的斜率很小)。如果你拓展了左尾的差异，减少了右尾的差异，结果将是方差恒定、形状对称的正态分布(无论均值大小如何)。

from scipy.special import boxcox1p
all_data[feat] = boxcox1p(all_data[feat], lam)