归一化&标准化
1、归一化是将数值放缩到[0, 1]或者[-1, 1]
常用于机器学习计算多个不同量纲的特征映射到[0, 1]或者[-1, 1],所以该值受有最大值和最小值决定
2、z-score
由于Z-score的数据分布满足“正态分布”(N(0,1)),而“正态分布”又被称为“Z-分布”,所以该方法被称为“Z-score”
Z-score是用于做数据规范化处理的一种方法
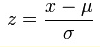
3、标准化是通过求z-score方法,将列特征转化为标准正太分布,和整体样本分布相关,每个样本点都能对标准化产生影响。
归一化和标准化共同点:都能取消由于量纲不同引起的误差;都是一种线性变换,都是对向量X按照比例压缩再进行平移。
除了归一化和标准化之外,还有中心化,也就是将数据的mean变成0.
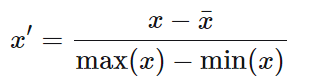
一般来说,工程上优先使用标准化,然后再归一化。
4、什么时候用归一化,标准化(参考:https://www.cnblogs.com/shine-lee/p/11779514.html)
涉及或隐含距离计算的算法,比如K-means、KNN、PCA、SVM等,一般需要feature scaling
1、zero-mean一般可以增加样本间余弦距离或者内积结果的差异,区分力更强,假设数据集集中分布在第一象限遥远的右上角,将其平移到原点处,可以想象样本间余弦距离的差异被放大了。在模版匹配中,zero-mean可以明显提高响应结果的区分度。
2、就欧式距离而言,增大某个特征的尺度,相当于增加了其在距离计算中的权重,如果有明确的先验知识表明某个特征很重要,那么适当增加其权重可能有正向效果,但如果没有这样的先验,或者目的就是想知道哪些特征更重要,那么就需要先feature scaling,对各维特征等而视之。
3、增大尺度的同时也增大了该特征维度上的方差,PCA算法倾向于关注方差较大的特征所在的坐标轴方向,其他特征可能会被忽视,因此,在PCA前做Standardization效果可能更好,如下图所示,图片来自scikit learn-Importance of Feature Scaling,
等等
5、什么时候不用归一化,标准化
- 与距离计算无关的概率模型,不需要feature scaling,比如Naive Bayes;
- 与距离计算无关的基于树的模型,不需要feature scaling,比如决策树、随机森林等,树中节点的选择只关注当前特征在哪里切分对分类更好,即只在意特征内部的相对大小,而与特征间的相对大小无关。





