3-分类
1、场景
- 根据用户的收入、贷款、年龄等特征 判断是否给用户发放贷款
- 根据病人的体检各项指标 判断是否患有癌症
- 各自手写字体的图片 判断是哪个字
2、求解方式
2.1 是否可以回归进行分类?

答案肯定不可以,
原因一,如下图右图所示,使用回归方法来进行分类任务,效果不好(最好的效果应该是左图的那根线);原因是定义回归好坏的loss function不适用于分类任务
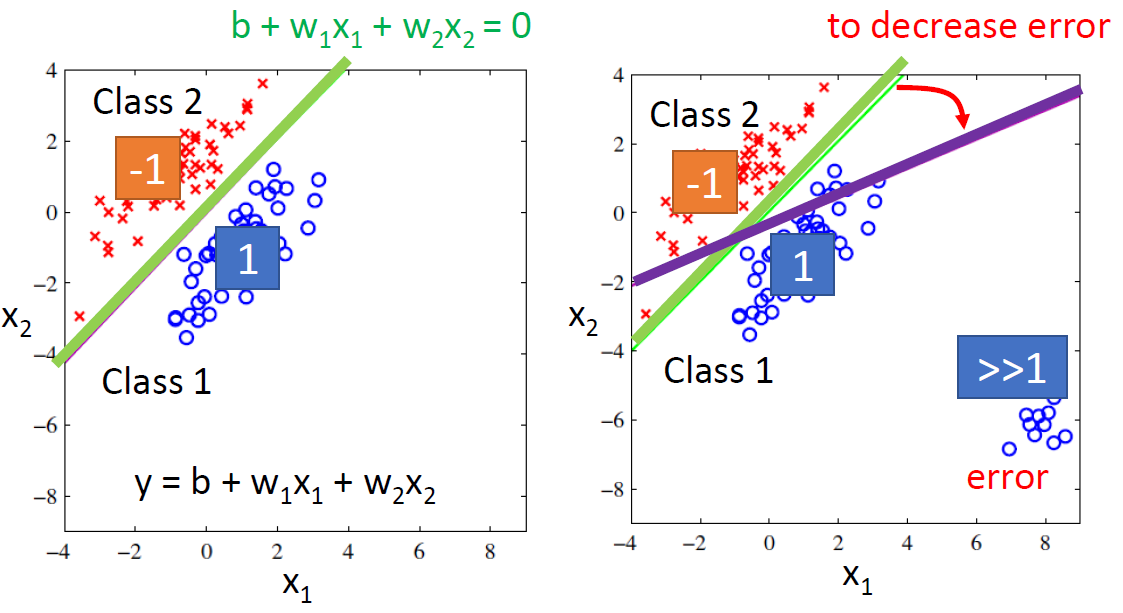
原因二:多分类如下,但是class1,class2,class3 并没有如下的大小关系,训练出来的效果肯定不好

2.1 正确的求解方法
2.1.1 建模

2.1.2 求解方式1
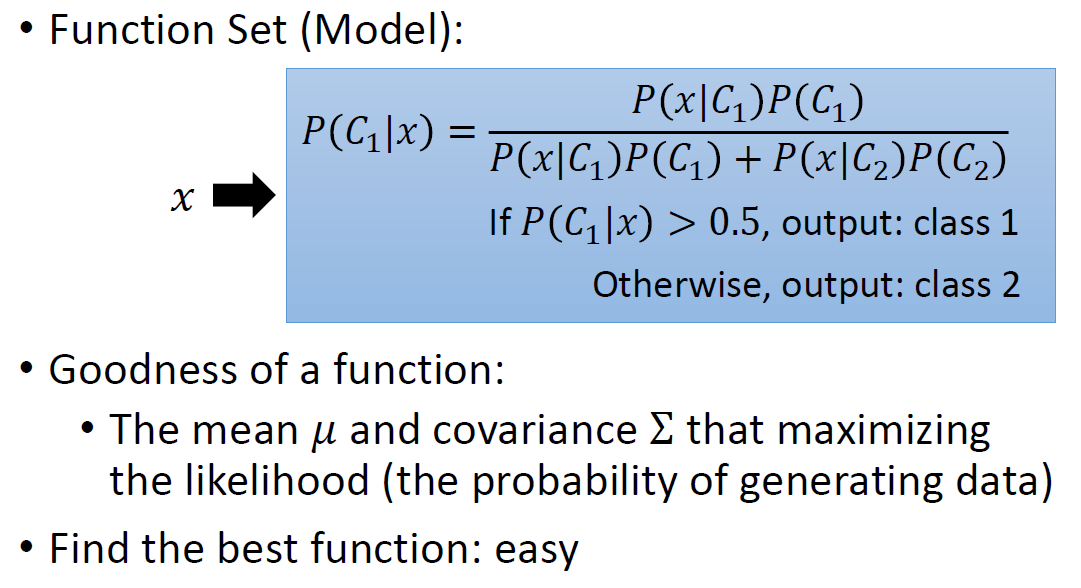
假设特征是服从几率模型,高斯分布

给定一系列的输入data(输入特征),任何一个高斯分布(不同的u和D)都可能产生这些输入的data,只是不同的高斯分布下的这些data的几率不同。

所以我们就是计算出那个u和D使得可能性最大

计算出了u和D,计算出输入的分布,则可以进行分类任务

最终的效果如下,从下图可以看到效果不好
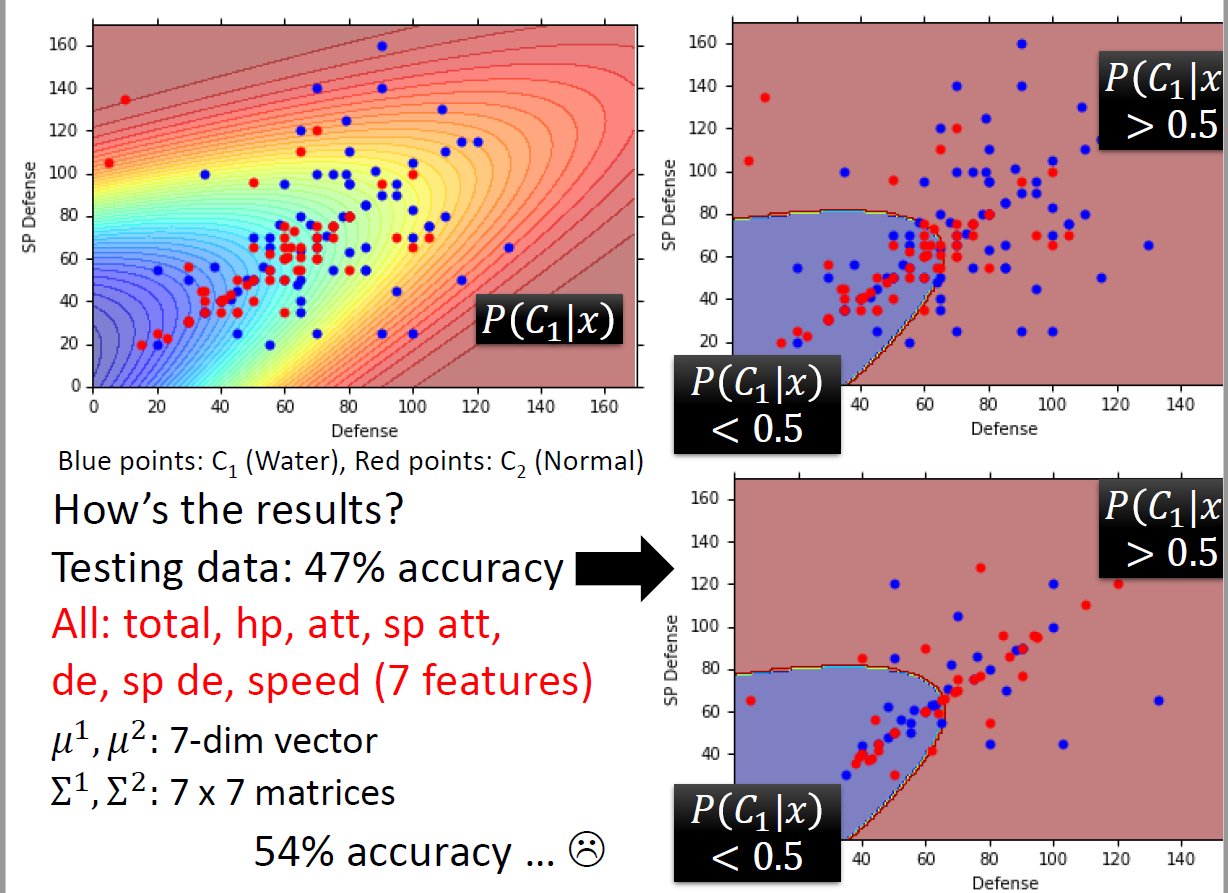
2.1.3 优化:如下2个类别分别训练不同的u和D,参数比较多,可能会过拟合,所有2个类别使用相同的D
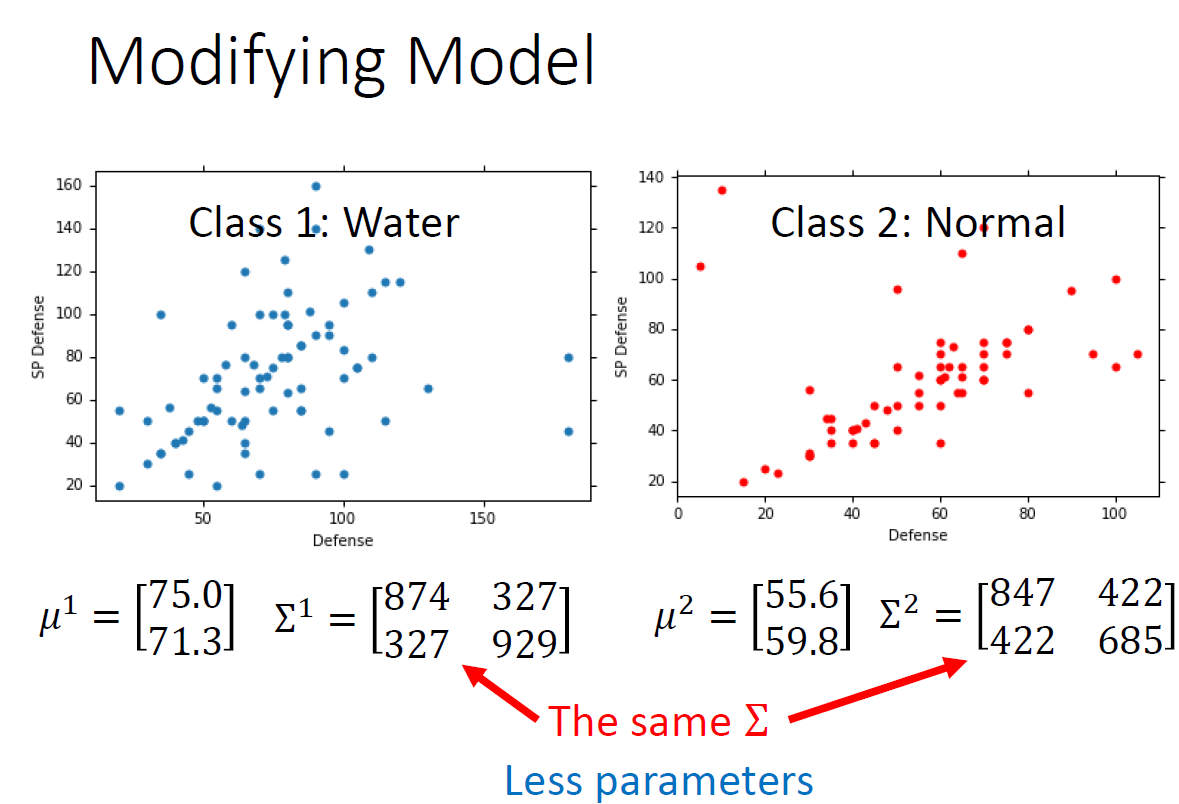
2.1.4 求解方式2
2.1.4.1 优化model
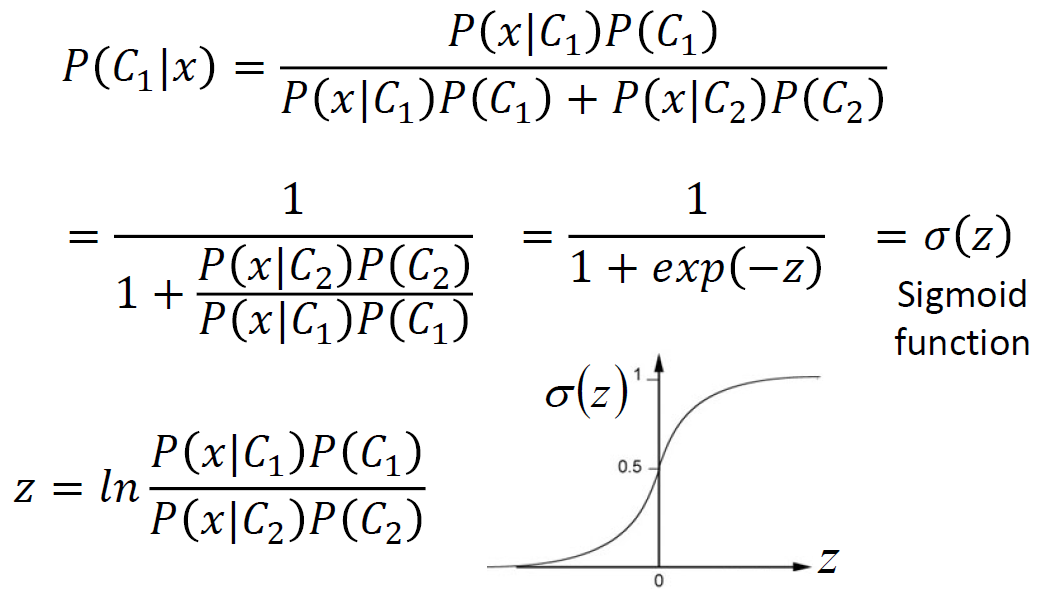




综上,与其找u1,u2,b然后计算w,和b,不如直接找最优的w,b
2.1.4.2 建模
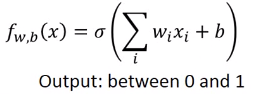
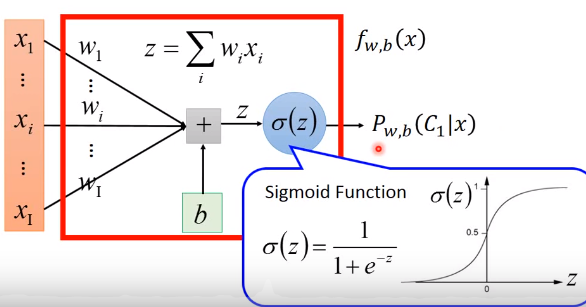
2.1.4.3 Loss(定义function的好坏)

由max L(w,b)转化为 min (-lnL(w,b))的目的是引入交叉熵


所以;

2.1.4.4 find best function
偏导数

2.1.4.4 和回归对比

2.1.4.4 分类不能使用回归的l2 loss

实例,判断工资是否大于5000(参考李宏毅)
https://archive.ics.uci.edu/ml/datasets/Census-Income+(KDD)
import numpy as np
import matplotlib.pyplot as plt
X_train_fpath = r"D:\work\ai\hung_li_2020\2_income\data\X_train"
Y_train_fpath = r"D:\work\ai\hung_li_2020\2_income\data\Y_train"
X_test_fpath = r'D:\work\ai\hung_li_2020\2_income\data\X_test'
output_fpath = r'D:\work\ai\hung_li_2020\2_income\data\output_{}.csv'
# *******************************read data
# 1 read normal
with open(X_train_fpath) as f:
next(f) # skip first line
X_train = np.array([line.strip().split(",")[1:] for line in f], dtype=float) # 第一个为序号
with open(Y_train_fpath) as f:
next(f) # skip first line
Y_train = np.array([line.strip().split(",")[1] for line in f], dtype=float) # 第一个为序号
with open(X_test_fpath) as f:
next(f) # skip first line
X_test = np.array([line.strip().split(",")[1:] for line in f], dtype=float) # 第一个为序号
print(X_train.shape)
print(Y_train.shape)
print(X_test.shape)
# 2 read by pandas
# import pandas as pd
# X_train = pd.read_csv(X_train_fpath).iloc[:, 1:] # read_csv把第一行为字段名
# Y_train = pd.read_csv(Y_train_fpath).iloc[:, 1:]
# X_test = pd.read_csv(X_test_fpath).iloc[:, 1:]
# print(X_train.shape)
# print(Y_train.shape)
# print(X_test.shape)
# *******************************normalize data -------------------------------------------------技巧1
def nomalize_(X, train=False, X_mean=None, X_std=None):
if train :
X_mean = np.mean(X, axis=0)
X_std = np.std(X, axis=0)
return (X - X_mean)/(X_std+1e-8), X_mean, X_std
X_train, X_mean, X_std = nomalize_(X_train, train=True)
X_test, _, _ = nomalize_(X_test, train=False, X_mean=X_mean, X_std=X_std)
# *******************************split train,dev data
from sklearn.model_selection import train_test_split
X_train, X_dev, Y_train, Y_dev = train_test_split(X_train, Y_train, test_size=0.1)
train_size = X_train.shape[0]
data_dim = X_train.shape[1]
dev_size = X_dev.shape[0]
test_size = X_test.shape[0]
print(X_train.shape, X_dev.shape, Y_train.shape, Y_dev.shape)
print(trian_size, data_dim, dev_size, test_size)
# ********************************model and loss
def sigmod_(y):
return np.clip(1/(1 + np.exp(-y)), 1e-8, (1-1e-8))
def cross_entropy_loss(y, y_):
# return sum(-(y_ * np.log(y)) - (1-y_)*np.log(1-y))
return -np.dot(y_, np.log(y)) - np.dot((1-y_), np.log(1-y))
def gradient(W, b, X, y_):
y = f_y(W, X, b)
pre_y = y_ - y
w_grad = -np.sum(pre_y * X.T, 1)
b_grad = -np.sum(pre_y)
return w_grad, b_grad
def f_y(W, X, b):
# print("W, X, b", W.shape, X.shape)
return sigmod_(np.dot(X, W)+b)
# ******************************* useful function
def shuffle(X, Y):
random_num = np.arange(len(X))
np.random.shuffle(random_num)
return X[random_num], Y[random_num]
# ****************************** result 评估
def accuracy(y_, y):
return 1 - np.mean(np.abs(y_ - y))
# ******************************* train
W = np.zeros((data_dim,))
b = np.zeros((1,))
steps = 50
learn_rate = 0.2
batch_size = 8
# Keep the loss and accuracy at every iteration for plotting
train_loss = []
dev_loss = []
train_acc = []
dev_acc = []
step = 1
for epo in range(steps):
# print("X_train, Y_train", X_train.shape, Y_train.shape)
# ********************************************* random train data and epoch ------------------------------技巧2
X_train, Y_train = shuffle(X_train, Y_train)
# print("X_train, Y_train", X_train.shape, Y_train.shape)
for idx in range(int(np.floor(train_size / batch_size))):
X = X_train[idx * batch_size: (idx+1) * batch_size]
Y = Y_train[idx * batch_size: (idx+1) * batch_size]
W_grad, b_grad = gradient(W, b, X, Y)
W = W - learn_rate / np.sqrt(step+1) * W_grad # 学习率逐渐减小 ----------------------------------技巧3
b = b - learn_rate / np.sqrt(step+1) * b_grad
step= step + 1
# train data loss and accurate
y = f_y(W, X_train, b)
y_ = np.round(y)
train_acc.append(accuracy(Y_train, y_))
train_loss.append(cross_entropy_loss(y,Y_train)/ train_size)
# dev data loss and accurate
y = f_y(W, X_dev, b)
y_ = np.round(y)
dev_acc.append(accuracy(Y_dev, y_))
dev_loss.append(cross_entropy_loss( y,Y_dev)/ dev_size)
import matplotlib.pyplot as plt
plt.plot(train_loss)
plt.plot(dev_loss)
plt.title('Loss')
plt.legend(['train', 'dev'])
# plt.savefig('loss.png')
plt.show()
plt.plot(train_acc)
plt.plot(dev_acc)
plt.title('Accuracy')
plt.legend(['train', 'dev'])
# plt.savefig('loss.png')
plt.show()
print('Training loss: {}'.format(train_loss[-1]))
print('Development loss: {}'.format(dev_loss[-1]))
print('Training accuracy: {}'.format(train_acc[-1]))
print('Development accuracy: {}'.format(dev_acc[-1]))



 浙公网安备 33010602011771号
浙公网安备 33010602011771号