C语言递归分析

思路

下图描述的是从问题引出到问题变异的思维过程：

概述

本文以数制转换为引，对递归进行分析。主要是从多角度分析递归过程及讨论递归特点和用法。

引子

一次在完成某个程序时，突然想要实现任意进制数相互转换，于是就琢磨，至少涉及以下参数：

  1. 源进制数：scr
  2. 目标进制：dest_d
    实现的大致思路：
    scr --> 数字分解 --> 按权求和 --> dest
    很明显这个过程是先正序分解，然后逆序求和，所以我就联想到了递归。

递归

1. 递归的含义

  1. 递归就是递归函数。递归函数是直接或间接调用自身的函数。

举个例子：

程序1: btoa.c
 1         /*
 2         ** 接受一个整型值（无符号），把它转换为字符并打印它，前导零被删除。
 3         */
 4       #include <stdio.h>
 5     void binary_to_ascii( unsigned int value ) {
 6         unsigned int quotient;
 7         quotient = value / 10;
 8         if( quotient != 0)
 9             binary_tc_ascii( quotient );
10         putchar( value % 10 + '0' );
11     }


另外递归还有所谓“三个条件”，“两个阶段”。我就不说了。实际应用时一般都很自然的满足条件。

2. 递归过程分析

  • 中断角度

看例：
有5人从左至右坐，右边人的年龄比相邻左边人大2岁，最左边的那个人10岁。问最右边人年龄。
    1. 程序2： age.c
    2.  1 #include <stdio.h>
 2 age(int n) {
 3     int c;
 4     if( n == 1 )
 5         c = 10;
 6     else
 7         c = age( n-1 ) + 2;
 8     return(c);
 9 }
10 
11 int main() {
12     printf("%d\n\n",age( 5 ) );
13     return 0;
14 }

       

表达式：

递推和回推过程：

　　这跟中断有什么联系呢？现在看来确实不很明显，不过最初我就是由它想到《微机原理》中的中断的：从age(5)开始执行，然后调用age(4),即来一个中断，此时先保护现场，然后一直递归直到n=1时，中断结束，然后层层返回，也就是不断恢复现场的过程。

  • 嵌套调用角度：
    嵌套调用关系图：

    看懂了这个图，把上面的fun_a()和fun_b()全换成一样的fun()，就相当于是递归时的函数对自身的调用过程。
    另外好像这幅图更容易看出“中断过程”吧。

  • 堆栈角度

    如果中断和嵌套这两个角度都看明白的话，这个堆栈角度就是升华一下。

    还用程序1为例进行分析：
    　　程序1的函数有两个变量：参数value和局部变量quotient。下面的一些图显示了堆栈的状态，当前可以访问的变量位于栈顶。所有其他调用的变量饰以灰色阴影，表示它们不能被当前正在执行的函数访问。
    　　假定我们以4267这个值调用递归函数。当函数开始执行时，堆栈的内容如下图所示。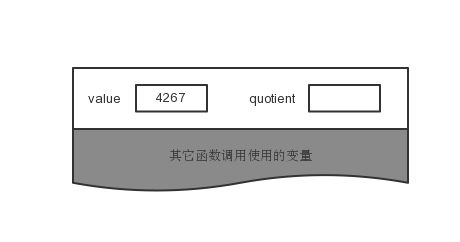
    e1.png
    　　执行除法运算之后，堆栈的内容如下：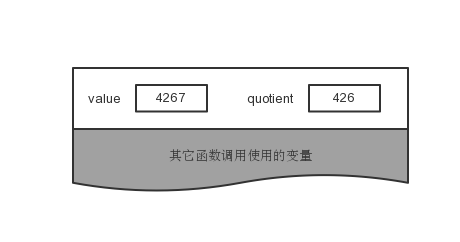
    e2.png
    　　接着，if语句判断出 quotient 的值非零，所以对该函数执行递归调用。当这个函数第二次被调用之初，堆栈的内容如下：
    e3.png
    　　堆栈上创建了一批新的变量，隐藏了前面的那批变量，除非当前这次递归调用返回，否则它们是不能被访问的。再次执行除法运算之后，堆栈的内容如下：
    e4.png
    　　quotient的值现在为42，仍然非零，所以需要继续执行递归调用，并再创建一批变量。在执行完这次调用的除法运算之后，堆栈的内容如下：
    e5.png
    　　此时，quotient的值还是非零，仍然需要执行递归调用。在执行除法运算之后，堆栈的内容如下：
    e6.png
    　　不算递归调用语句本身，到目前为止所执行的语句只是除法运算以及对quotient的值进行测试。由于递归调用使这些语句重复执行，所以它的效果类似循环：当quotient的值非零时，把它的值作为初始值重新开始循环。但是，递归调用将会保存一些信息（这点与循环不同），也就是保存在堆栈中的变量值。这些信息很快就会变得非常重要。
    　　现在quotient的值变成了零，递归函数便不再调用自身，而是开始打印输出。然后函数返回，并开始销毁堆栈上的变量值。
    　　每次调用putchar得到变量value的最后一个数字，方法是对value进行模10余运算，其结果是一个0~9之间的整数。把它与字符常量'0'相加，其结果便是对应于这个数字的ASCII字符，然后把这个字符打印出来。
    t1.png
    　　接着函数返回，它的变量从堆栈中销毁。接着，递归函数的前一次调用重新继续执行，它所使用的是自己的变量，它们现在位于堆栈的顶部。因为它的value值是42，所以调用putchar后打印出来的数字是2 。
    t2.png
    　　接着递归函数的这次调用也返回，它的变量也被销毁，此时位于堆栈顶部的是递归函数再前一次调用的变量。递归调用从这个位置继续执行，这次打印的数字是6 。在这次调用返回之前，堆栈的内容如下：
    t3.png
    　　现在我们已经展开了整个递归过程，并回到该函数最初的调用。这次调用打印出数字7，也就是它的value参数除10的余数。
    t4.png
    　　然后，这个递归函数就彻底返回到其他函数调用它的地点。
    　　如果你把打印的字符一个接一个排在一起，出现在打印机或屏幕上，你将看到正确的值4267 。

  • 3. 递归的应用

    　　上面从不同角度对递归过程进行了分析。而际应用时并不要求你搞清楚每个递归的内部过程，重要的是用对。
    　　下面主要是不恰当应用递归的一些例子：
    　　许多教材中都把计算阶乘和菲波那契数列用来说明递归，然而前者中递归并没有提供任何优越之处，后者中递归的效率非常之低。
    　　看一下极端的菲波那契数求解：
    　　表达式：
    　　
    　　这种递归形式的定义容易诱导人们使用递归形式来解决问题：

    程序3：fib_rec.c
    1 /*
2 ** 用递归方法计算第n个菲波那契数列的值。
3 */
4 
5 int fibonacci( int n ) {
6     if( n <= 2 )
7         return 1;
8     return fibonacci( n - 1 ) + fibonacci( n - 2 );
9 }

     

    　　这里有一个陷阱：它使用递归步骤计算fibonacci( n -1)和 fibonacci( n -2)。但是，在计算 fibonacci( n -1)时也将计算 fibonacci( n -2)。这个额外的代价有多大呢？　　答案是：它的代价远远不止一个冗余计算：每个递归调用都会触发另外两个递归调用，面这两个调用的任何一个还并将触发两个递归调用，再接下去的调用也是如此。这样，冗余计算的数量增长得非常快。例如，在递归计算fibonacci(10)时，fibonacci(3)的值被计算了21次。但是在递归计算fibonacci(30)时，fibonacci(3)的值被计算了317811次，当然，这317811次产生的结果是完全一样的，除了其中之一外，其余的纯属浪费。
    1. 　　想得更极端一些，假如你在程序中递归时不是两次而是3次，4次，更多次的调用自身，那我想可能会让程序崩溃吧。
    2. 　　现在让我们尝试用循环代替递归：
    3. 程序4：fib_iter.c
 1 int fibonacci( int n ) {
 2     int result;
 3     int previous_result;
 4     int next_older_result;
 5     result = previous_result = 1;
 6     while(n > 2 ) {
 7         n -= 1;
 8         next_older_result = previous_result;
 9         previous_result = result;
10         result = previous_result + next_older_result;
11     }
12     return result;
13 }

  2. 　　OK，说到这了，本文引子是数制转换，总得说点数制转换点题是吧。
　嗯，把题目都忘记了，回引子看一下吧。
程序5：convert.c
 1 #ifndef _CONERT_H
 2     #define _CONERT_H
 3     #include <stdio.h>
 4     #include <math.h>
 5 #endif
 6 
 7 /*
 8 **main()
 9 */
10 
11 int conert2any( int scr, int dest_d, int pow_base ) {
12 /*
13 ** 调用该函数时参数pow_base必须为0
14 */
15     int quotient, result;
16     int dest_d_base = 10;
17     quotient = scr / dest_d;
18     if( quotient != 0 )
19         result = ( scr % dest_d ) * pow( dest_d_base, pow_base) + conert2any( quotient, dest_d, ++pow_base );
20     else
21         result = ( scr % dest_d ) * pow( dest_d_base, pow_base);
22     return ( result );
23 }

 

OK，这个数制转换程序用递归实现，没什么问题，但受上例启发它也可以改为循环：

程序6：convert_loop.c
1 do {
2     result += (scr % dest_d ) * pow( dest_d_base, pow_base++ );
3 } while( scr /= dest_d != 0 )

 

  相比于递归，它更短小精悍，效率也高些。

　　经过两个递归改为循环的例子，你应该发现这两个例子有一个共同点：递归调用时最后执行的语句是return 。
　　对于这种调用时最后执行的是return的递归，有一种专门的称呼：尾部递归。
　　可以发现一般情况下尾部递归都可以改为相应的循环形式，而且更简洁高效。
　　那什么时候才必须用递归呢？据我目前的经验和思考，只有程序1－－逆序打印是必须的，其它好像没有必须用递归的。
好了，到这递归也告一段落了，来个小插曲，谈一下我写程序5时的一些感受：
　　实现这个进制转换函数时，对递归的理解还不深，犯了现在看来可笑的错误：其中要用递归实现加权求和，我还曾苦思如何实现累加呢，每一次调用完后变量都销毁了，如何累加呢？苦思的结果是：利用静态变量保存累加的值。如果到此为止的话我也不会进一步学习递归。因为我想，虽然这样能实现，可是不完美，即便碧波函数调用完了，静态变量依然在占着空间，而且再次调用前还得先清零。C语言的递归不该是如此麻烦的，一定是我哪里想差了，于是我就反复看书上的例子，终于醒悟：直接用return返回不就可以实现累加了嘛。唉，当时脑子真是灌了浆糊了。

 

言归正传，全文结束，对递归总结一下：

  1. 递归即是函数对自身的嵌套调用。
  2. 一般情况下尾部递归是不必要的，用循环会更好。
  3. 用递归分析重复过程层次分明，所以最好用先用递归分析，然后转用循环去实现。

     

说明：

  1. 程序1,3,4 引自《C和指针》7.5
  2. 程序2 引自 本校教材《C语言程序设计》7.4
  3. “堆栈角度” 引自 《C和指针》7.5

     

date: 2014-12-10



 

 

 

posted @ 2014-12-11 22:38  yufenga  阅读(11240)  评论(0)  编辑  收藏  举报