【题解】前k大子段和
题目描述
Peter喜欢玩数组。NOIP这天,他从Jason手里得到了一个大小为\(n\)的数组。
Peter求出了这个数组的所有子段和,并将这\(\frac{n(n+1)}{2}\)个数降序排列,他想知道前\(k\)个数是什么。
输入输出格式
输入格式
输入数据的第一行包含两个整数\(n\)和\(k\)。
接下来一行包含\(n\)个整数,代表数组。
输出格式
输出\(k\)个数,代表降序之后的前\(k\)个数,用空格隔开。
数据范围
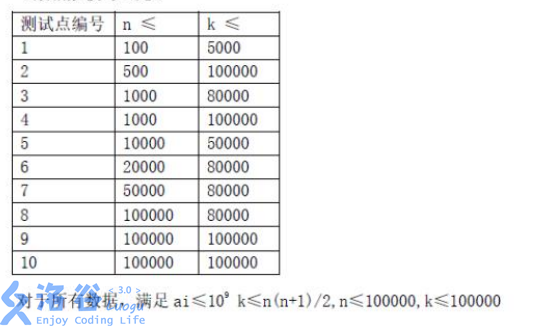
题解
这个题目说的是十分的简洁明了,要求我们求出所有的子段和中前\(k\)大,首先看到这道题的时候,我用的二分答案加树状数组维护虽然在这道题上这种方法会T飞,但是,这种方法是一种方法是一种十分有效的算法。我们先二分答案来枚举第\(k\)大的子段和, 然后再用树状数组来维护和查询(就有点像求逆序对)。
具体过程:
我们每次枚举时,出第\(k\)大子段和为\(x\),那么\(x\)一定可以被表示为\(x = sum[i] - sum[j - 1]\)(\(sum[i]\)表示前缀和),我们把这个式子移项,可以得到\(sum[j - 1] = sum[i] - x\),这个式子表示当我们遍历到第 \(i\)个前缀和时,已知第\(k\)大的子段和为\(x\)那么我们只用找到\(sum[j - 1]\)之前有多少个\(sum[]\)就可以知道有多少个子段和比\(x\)大了。
#include<bits/stdc++.h>
using namespace std;
#define lowbit(x) ((x) & (-x))
const int MAX = 100005;
int n, k;
long long a[MAX], sum[MAX], tree[MAX];
vector <long long> s;
void Add(int x, long long val)
{
for(; x <= n; x += lowbit(x)) tree[x] += val;
}
long long Query(int x)
{
long long ret = 0;
for(;x ; x-= lowbit(x)) ret += tree[x];
return ret;
}
int check(int mid)
{
int ret = 0;
memset(tree, 0, sizeof(tree));
for(int i = 1; i <= n; ++ i)
{
int x = sum[i] - mid;
int it = lower_bound(s.begin(), s.end(), x) - s.begin();
ret += Query(it);
if(x > 0) ret ++;
it = lower_bound(s.begin(), s.end(), sum[i]) - s.begin();
Add(it + 1, 1);
}
return ret;
}
int main()
{
// freopen("ksum.in", "r", stdin);
// freopen("ksum.out", "w", stdout);
scanf("%d%d", &n, &k);
for(int i = 1; i <= n; ++ i)
{
scanf("%d", &a[i]);
sum[i] = sum[i - 1] + a[i];
s.push_back(sum[i]);
}
sort(s.begin(), s.end());
for(int t = 1; t <= k; ++ t)
{
long long l = 0, r = sum[n], mid, ans = 0;
for(;l < r;)
{
mid = (l + r) >> 1;
if(check(mid) >= t) l = mid + 1;
else r = mid;
}
printf("%lld ", l);
}
return 0;
}
如果求取的次数比较少的话,这也会是一个优秀的算法,但是,这道题的\(k\)太大,导致要多次重复这个过程所以,我们要考虑其他解法,因为数组中的数都是非负数,所以,我们可以来贪心。
- 最大的一定是所有数之和。
- 每次将最大的去头或去尾可以构成备选答案。
所以我们可以用优先队列来维护,但是,对于\([x,y]\)来说,它可能在\([x - 1, y]\)去头时加入,也有可能在\([x,y + 1]\)去尾时加入,这样就会重复,所以,我们需要一种不会重复的枚举方式,我们把所有前缀和入队,然后每次只考虑去头而不考虑去尾(在前缀和入队时已经去过了),这样就不会重复了。
#include<bits/stdc++.h>
using namespace std;
struct Node{
int l, r;
long long sum;
bool friend operator < (const Node & x, const Node & y)
{
return x.sum < y.sum;
}
};
priority_queue <Node> q;
long long a[100005], sum = 0;
Node make_Node(int l, int r, long long sum)
{
Node x;
x.l = l, x.r = r, x.sum = sum;
return x;
}
int main()
{
int n, k;
scanf("%d%d", &n, &k);
for(int i = 1; i <= n; ++ i)
{
scanf("%d", &a[i]);
sum += a[i];
q.push(make_Node(1, i, sum));
}
for(int i = 1; i <= k; ++ i)
{
Node x;
x = q.top(); q.pop();
printf("%lld ", x.sum);
q.push(make_Node(x.l + 1, x.r, x.sum - a[x.l]));
}
printf("\n");
return 0;
}


