【洛谷P3410】拍照题解(最大权闭合子图总结)
题目描述
小B有n个下属,现小B要带着一些下属让别人拍照。
有m个人,每个人都愿意付给小B一定钱让n个人中的一些人进行合影。如果这一些人没带齐那么就不能拍照,小B也不会得到钱。
注意:带下属不是白带的!!!对于每个下属,如果他带了那么小B需要给他一些钱,保证当他拍照时配合。
请问,小B的净收益最多是多少。
输入输出格式
输入格式:
第1行有2个正整数m和n(0<m,n<=100)。接下来的m行,每行是一个要求拍照的人的有关数据。第一个数是他同意支付该合影的费用;接着是该合影需要的若干下属的编号,以一个0作为行的结束标记。最后一行的n个数是带每个下属的费用。
输出格式:
一个数,表示最大收益。小B可以一个人也不带。
题解
我们把题目用图的形式表示出来:我们把所有的要求看作是点,每个要求的收益看作是这个点的点权,同理每个人也看作是点,每个人的花费的相反数看作是这个点的点权,然后在每个要求与人之间连接有向边。
就可发现,我们所求的其实就是这个图的最大权闭合子图。
首先,我们先来解释一下什么叫做闭合图,所谓最大权闭合图指的是对于一个点集,从这个点集中的点出发的所有出边所指向的点也在这个点集中,则这个点集所组成的图就是一个闭合图。举个例子来说:如下图所示,点集{1,2,3,4,5}和点集{1,2,3,4,5,6}所组成的图都是闭合图,而点集{1,2,3,5,6}就不是一个闭合图(6有一条出边指向了4,但是4没在点集中)。而所谓的最大权,就是指的这样的图中点权和最大的。
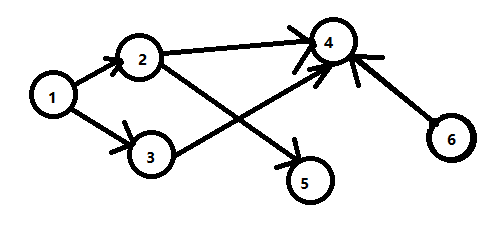
求解最大权的闭合子图我们通常是利用网络流进行求解,我们构造一个超级源点(s),把所有的点权为正的点都与之连边,边的容量为这些点的点权;再构造一个超级汇点(t),把所有的点权为负的点都与之连边,边的容量为点权的相反数,另外,这些点之间原有的边保持不变,边的容量为正无穷。即如下图(黑色为点的编号,红色为权值):
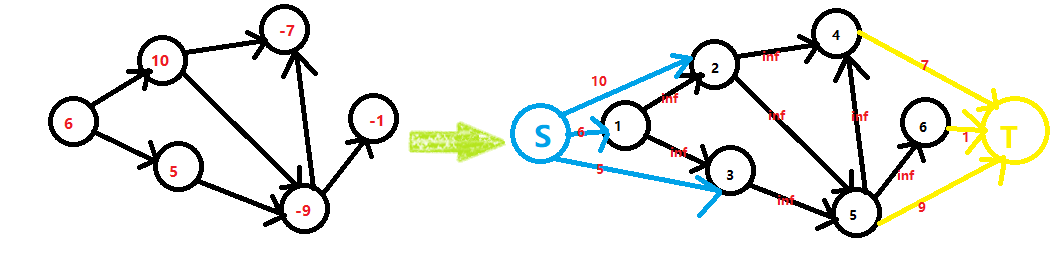
我们来研究以下两个图之间有什么关系:
- 在第二个图中,关于s-t的最小割是简单割(割边都与S或T相连),显然他不会去割无穷大的边(黑色的边)。
- 第二个图的关于s-t的每一个简单割产生的两个子图,我们把含有S的称作S图,含有T的称作T图。则S图是闭合子图。
证明:
简单割中不包含无穷大的边(黑色的边),即不包含联通两个图的边(连接在T点上的边除外)。所以S图中的边所指向的点一定在S图中,即为闭合图。
- 最小割产生的S图和T图,S图为最大权闭合子图。
证明:
因为割集中所有的边,不是连接在s上,就是连接在t上;
我们记割集中,所有连接在s上的边的权值和为x1,所有连接在t上的边的权值和为x2,而割集中所有边权值和为X=x1+x2;
又,记图S中所有点的权值和为W,记其中正权值之和为w1,负权值之和为 - w2,故W = w1 - w2;
而 W + X = w1 - w2 + x1 + x2,由于x2 = w2
(因为图S中所有负权值的点,必然连接到t点,而图S必然要与t分割开;故割集中,“连接在t点上的边权值和”就是“图S中所有负权值点的权值之和,取负”)
因而W + X = w1 + x1;
而显然的,w1 + x1是整个图中所有正权值之和,记为SUM;
故W = SUM - X,即 “图S中所有点的权值和” = “整个图中所有正权值之和” - “割集中所有边权值和”;
然后,因为SUM为定值,只要我们取最小割,则“图S中所有点的权值和”就是最大的,即此时图S为图S为最大权闭合子图。
所以最大权闭合子图的点权之和等于收益点权之和减去最小割。
代码
#include<bits/stdc++.h> using namespace std; int w[105], c[105]; vector <int> G[105]; int n, m, x; const int inf = 0x7fffffff; class Graph{ private : int cnt; int Head[205], Next[100005], W[100005], To[100005]; int Deep[205], cur[205]; public : int s, t, n; void init() { cnt = -1; memset(Head, -1, sizeof(Head)); memset(Next, -1, sizeof(Next)); } void _Add(int u, int v, int c) { Next[++ cnt] = Head[u]; Head[u] = cnt; W[cnt] = c; To[cnt] = v; } void Add_edge(int x, int y, int w) { _Add(x, y, w); _Add(y, x, 0); } int Dfs(int u, int flow) { if(u == t) return flow; for(int & i = cur[u]; i != -1; i = Next[i]) { if(Deep[To[i]] == Deep[u] + 1 && W[i] != 0) { int di = Dfs(To[i], min(flow, W[i])); if(di > 0) { W[i] -= di; W[i ^ 1] += di; return di; } } } return 0; } int Bfs() { queue <int> q; for(; !q.empty();) q.pop(); memset(Deep, 0, sizeof(Deep)); Deep[s] = 1; q.push(s); for(; !q.empty();) { int u = q.front(), v; q.pop(); for(int i = Head[u]; i != -1; i = Next[i]) if(!Deep[v = To[i]] && W[i]) { Deep[v] = Deep[u] + 1; q.push(v); } } return Deep[t] > 0 ? 1 : 0; } int Dinic() { int ans; for(;Bfs();) { for(int i = 1; i <= n; ++ i) cur[i] = Head[i]; int d; for(;d = Dfs(s, inf);) ans += d; } return ans; } }; Graph Map; int Num = 0; int n1[105], n2[105]; void Make_picture() { Map.s = ++ Num; for(int i = 1; i <= n; ++ i) { n1[i] = ++ Num; Map.Add_edge(Map.s, Num, w[i]); } for(int i = 1; i <= m; ++ i) n2[i] = ++ Num; Map.n = Map.t = ++ Num; for(int i = 1; i <= m; ++ i) Map.Add_edge(n2[i], Map.t, c[i]); for(int i = 1; i <= n; ++ i) for(int j = 0; j < G[i].size(); ++ j) Map.Add_edge(n1[i], n2[G[i][j]], inf); return ; } int sum = 0; int main() { scanf("%d%d", &n, &m); for(int i = 1; i <= n; ++ i) { scanf("%d", &w[i]); sum += w[i]; for(;;) { scanf("%d", &x); if(!x) break; G[i].push_back(x); } } for(int i = 1; i <= m; ++ i) scanf("%d", &c[i]); Map.init(); Make_picture(); printf("%d\n", sum - Map.Dinic()); return 0; }
参考资料
[1]Dilthey's Blog:最大权闭合子图-[求最大点权的闭合子图]
[2]洛谷【P3410】拍照


