矩阵乘法

矩阵乘法

　　对于矩阵A（m*n）和一个矩阵B（n*p）相乘可以得到一个矩阵C（m*p），定义如下

　　

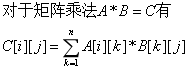
　　矩阵乘法满足结合律和分配率，但不满足交换律。

矩阵乘法加速递推

　　矩阵乘法中一种特殊的情形，F是一个1*n的矩阵，A是一个n*n的矩阵，F'=F*A也是一个1*n的矩阵。F和F'可看作一维数组，省略他们的行下标1。按照矩阵乘法的定义，任意的 j ∈ [1, n] ，有表示的含义是，进过一次与A的矩阵乘法后，F数组中第k个值会以A[k][j]为系数累加到F'数组上第j个值上，等价于在一个向量的k, j两个状态之间发生了递推。

　　所以我们可以利用矩阵乘法加速递推。

　　所以对于具有以下特点的题，我们可以利用矩阵加速乘法来加速递推：

1. 1. 可以抽象为一个长度为n的一维向量，该项量在每个单位时间内只发生一次变化。
   2. 变化的形式是线性递推（只有若干“加法”或“乘以一个系数“的运算）。
   3. 该递推式在每个时间可能作用于不同的数据上，但本身保持不变。
   4. 向量的变化时间(即递推轮)很长，但向量长度n很小。

　　我们在这儿做出以下定义

1. 1. 状态矩阵：长度为n的一维向量。
   2. 转移矩阵：用于与状态矩阵相乘的固定不变的矩阵A。

　　如若状态矩阵的第x个数对下一个单位时间的状态矩阵的第y个矩阵产生影响，我们就把转移矩阵的A[x][y]处赋予适当的系数，然后用矩阵快速幂完成。

 

矩阵快速幂

struct Matrix
{
    int Transition_Matrix[][] ;
    Matrix friend operator * (Matrix a, Matrix b)
        {
            Matrix c;
            memset(c.Transition_Matrix, 0, sizeof(c.Transition_Matrix));
            for(int i = 0; i < 16; ++ i)
                for(int j = 0; j < 16; ++ j)
                    for(int k = 0; k < 16; ++ k)
                        c.Transition_Matrix[i][j] = (c.Transition_Matrix[i][j] + a.Transition_Matrix[i][k] * b.Transition_Matrix[k][j] % mod) % mod;
            return c;
        }
    Matrix friend operator % (Matrix a, int mod)
        {
            for(int i = 1; i < 16; ++ i)
                for(int j = 1; j < 16; ++ j)
                    a.Transition_Matrix[i][j] = a.Transition_Matrix[i][j] % mod;
            return a;
        }
    Matrix ksm(Matrix a, int b)
    {
        Matrix res;
        memset(res.Transition_Matrix, 0, sizeof(res));
        for(int i = 0; i < 16; ++ i)    res.Transition_Matrix[i][i] = 1;
        for(;b; b >>= 1, a = (a * a) % mod)
            if(b & 1)    res = (res * a) % mod;
        return res;     
    }
};