LeetCode 221. 最大正方形 （巧妙DP，数学公式证明推导DP）

LeetCode 221. 最大正方形 （巧妙DP，公式证明推导DP）

题目描述

在一个由 0 和 1 组成的二维矩阵内，找到只包含 1 的最大正方形，并返回其面积。

动态规划\(O\left(n^{2}\right)\)

f[i, j]表示：所有以(i,j)为右下角的且只包含1 的正方形的边长最大值。

如下图，从(i,j)沿着对角线走，可以很容易的推断出f[i][j]受限于f[i-1][j](红色正方形)和f[i][j-1]（黄色正方形），但是其实还受限制于f[i - 1][j - 1]黑色正方形，如第二张图。

数学证明：

1. \(f[i][j] <= f[i - 1][j] + 1\),可以到映射到图中看一下，黄色部分+深蓝色部分假设为f[i][j]的正确矩形，即\(f[i][j] = f[i][j-1] + 2\),那么f[i- 1] [j] 一定可以在扩大一圈。其他\(f[i][j] <= f[i][j - 1] + 1, f[i][j] <= f[i - 1][j - 1] + 1\) 都是同样的道理。即导出公式
   \[f[i][j] <= min(f[i - 1][j], f[i][j - 1], f[i - 1][j - 1]) + 1 \]

如图：

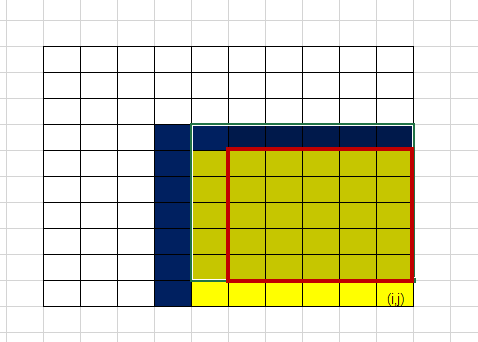
2. 接下来明确思路，只需要证明下面格式即可推出

   \[f[i][j] <= min(f[i - 1][j], f[i][j - 1], f[i - 1][j - 1]) + 1\\ f[i][j] >= min(f[i - 1][j], f[i][j - 1], f[i - 1][j - 1]) + 1\\ =>f[i][j] = min(f[i - 1][j], f[i][j - 1], f[i - 1][j - 1]) + 1 \]

   采用反证法：

   \[f[i][j] < min(f[i - 1][j], f[i][j - 1], f[i - 1][j - 1]) + 1\\ => f[i][j] <= min(f[i - 1][j], f[i][j - 1], f[i - 1][j - 1]) \]

   与下图矛盾

   

   时间复杂度\(O\left(n^{2}\right)\)

   空间复杂度\(O\left(n^{2}\right)\)

C++代码

class Solution {
public:
    int maximalSquare(vector<vector<char>>& matrix) {
        if (matrix.empty() || matrix[0].empty()) return 0;
        int n = matrix.size(), m = matrix[0].size();
        vector<vector<int>> f(n + 1, vector<int>(m + 1));

        int res = 0;
        for (int i = 1; i <= n; i ++ )
            for (int j = 1; j <= m; j ++ )
                if (matrix[i - 1][j - 1] == '1') {
                    f[i][j] = min(f[i - 1][j], min(f[i][j - 1], f[i - 1][j - 1])) + 1;
                    res = max(res, f[i][j]);
                }

        return res * res;
    }
};