Acwing 3823. 寻找字符串 KMP知识点回顾

题意

给定一个由小写字母构成的字符串 s。

请你找到一个满足如下所有要求的字符串 t：

• 字符串 t 是字符串 s 的前缀。
• 字符串 t 是字符串 s 的后缀。
• 字符串 t 在字符串 s 的中间出现过。也就是作为一个既非前缀也非后缀的子串出现过。
• 字符串 t 的长度应尽可能长。

输入格式
第一行包含整数 T，表示共有 T 组测试数据。

每组数据占一行，包含一个字符串 s。

输出格式
每组数据输出一行结果，如果 t 存在，则输出 t，否则输出 not exist。

数据范围
前三个测试点满足 1≤|s|≤20。
所有测试点满足 1≤T≤10，1≤|s|≤106。
同一测试点内所有输入字符串 s 的长度之和不超过 106。

输入样例：
2
fixprefixsuffix
abcdabc
输出样例：
fix
not exist

题解

KMP知识点

KMP核心：主串str[i]与模式串s[j]失配的时候，模式串j= next[j]开始匹配，而不是从头开始匹配。
next[i]表示s[1~i]的最长前后缀长度。

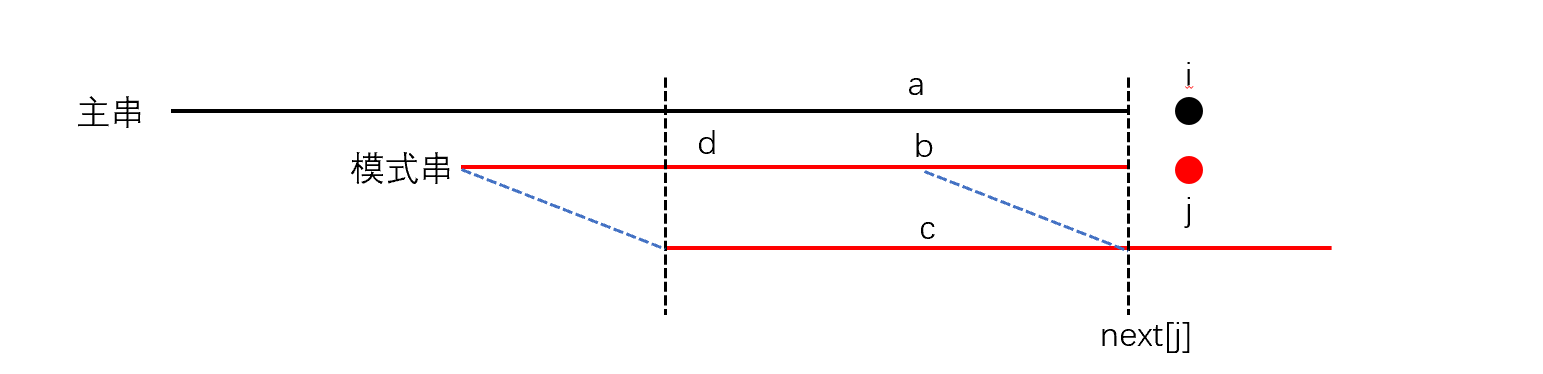
如图，a=b=d=c
从b=d可以看出，next模式前后缀长度，next肯定越大越好，因为j=next[j]回溯到模式串离自己越近越好。所以我们可以推出重要结论：最长前后缀长度为l1 = ne[n]，次长前后缀长度为l2 = ne[l1]，第三长为l3 = ne[l2]…以此类推直至为零

如上可以求出最长前后缀，中间的如何保证呢？
假设ne[i] = k,如果k在ne[1~n-1]出现过ne[i] == k,则中间一定出现过。

---

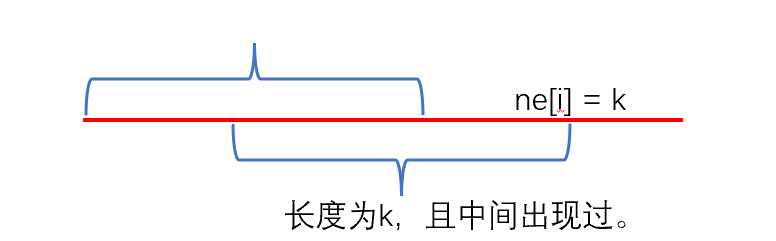
该题步骤：

1. 先求出ne数组
2. 然后标记st从1 ~ n - 1的最长前后缀的长度
3. 从大到小枚举前后缀长度，若发现从2 ~ n - 1中有中间缀，则求得答案

#include<bits/stdc++.h>
using namespace std;
const int N = 1e6 + 5;
char s[N];
int ne[N];
bool st[N];
int main()
{
    int T;
    cin>>T;
    while(T--)
    {
        scanf("%s",s+1);
        int n =strlen(s+1);
        string res = "not exist";
        for(int i = 2, j = 0; i <= n; i++){
            while(j&&s[i] != s[j + 1]) j = ne[j];
            if(s[i] == s[j + 1]) j++;
            ne[i] = j;
        }
        for(int i = 0; i <= n; i++) st[i] = false;
        for(int i = 1; i < n; i++) st[ne[i]] = true;
   
        for(int i = ne[n]; i; i = ne[i])
            if(st[i]){
                s[i + 1] = 0;
                res = s + 1;
                break;
            }
        cout<<res<<endl;
    }

    return 0;
}