拟合算法

学习视频：【强烈推荐】清风：数学建模算法、编程和写作培训的视频课程以及Matlab

老师讲得很详细，很受用！！！

定义

​ 与插值问题不同，在拟合问题中不需要曲线一定经过给定的点。拟合问题的目标是寻求一个函数（曲线），使得该曲线在某种准则下与所有的数据点最为接近，即曲线拟合的最好（最小化损失函数）。

插值和拟合的区别

​ 插值：样本数n<30

​ 拟合：样本数n>=30(大样本)

插值算法中，得到的多项式f(x)要经过所有样本点。但是如果样本点太多，那
么这个多项式次数过高，会造成龙格现象。
尽管我们可以选择分段的方法避免这种现象，但是更多时候我们更倾向于得到
一个确定的曲线，尽管这条曲线不能经过每一个样本点，但只要保证误差足够小即
可，这就是拟合的思想。 (拟合的结果是得到一个确定的曲线)

评价拟合效果

y_hat= k*x+b; % y 的拟合值 
SSR = sum((y_hat-mean(y)).^2)  % 回归平方和 
SSE = sum((y_hat-y).^2)     % 误差平方和 
SST = sum((y-mean(y)).^2) % 总体平方和 
SST-SSE-SSR R_2 = SSR / SST
%注： mean() 是求均值的函数

强大的曲线拟合工具箱

模拟数据代码

% （1）randi : 产生均匀分布的随机整数（i = int）  
%产生一个1至10之间的随机整数矩阵，大小为2x5；
s1 = randi(10,2,5)
%产生一个-5至5之间的随机整数矩阵，大小为1x10；
s2 = randi([-5,5],1,10)

%  （2） rand: 产生0至1之间均匀分布的随机数
%，产生一个0至1之间的随机矩阵大小为1x5；
s3 = rand(1,5)
%产生一个a至b之间的随机矩阵，大小为1x5；  % a + (b-a) * rand(1,5); 如：a,b = 2,5
s4= 2 + (5-2) * rand(1,5)

% （3）normrnd:产生正态分布的随机数
%产生一个均值为0，标准差（方差开根号）为2的正态分布的随机矩阵，大小为3x4；
s5 = normrnd(0,2,3,4)

% （4）roundn—任意位置四舍五入
% 0个位 1十位  2百位 -1小数点后一位  
a = 3.1415
roundn(a,-2)    % ans   =  3.1400
roundn(a,2)      % ans   =  0
a =31415
roundn(a,2)   % ans  = 31400
roundn(5.5,0)  %6
roundn(5.5,1) %10

模拟数据进行演示

\[y_{i}=3e^{0.5x_{i}}-5+e_{i} \]

xi是[0，10]上的均匀分布，\(e^{i}\)是标准正态分布的扰动项

clear;clc 
x = rand(30,1) * 10;  % x是0-10之间均匀分布的随机向量（30个样本）
y = 3 * exp(0.5*x) -5 + normrnd(0,1,30,1);
cftool

优秀论文中的cftool运用

cftool的‘骚’操作

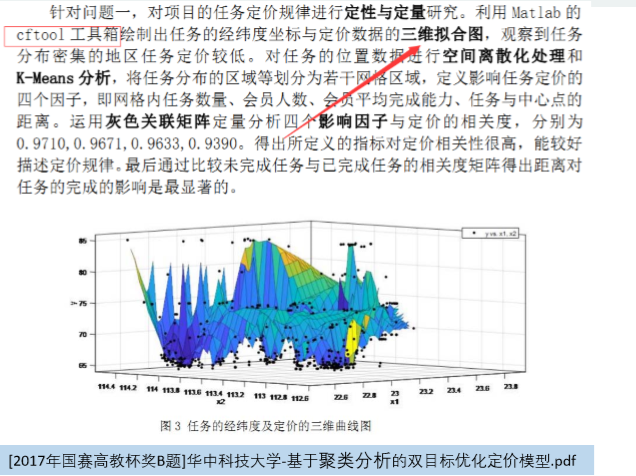
作业

题目

根据data2中的中国人口数据，确定你认为最合适 的拟合函数，并说明原因。

模型的建立

拟合算法简介

拟合指的是已知一系列的点，通过调整某些函数的待定系数使该函数与已知点集的差别最小。如果待定函数是线性，就叫线性拟合，否则称为作非线性拟合。若表达式也可以是分段函数，这种情况下称作样条拟合。

确定拟合函数

第一步：作出人口数量的散点图，结果如下图所示：

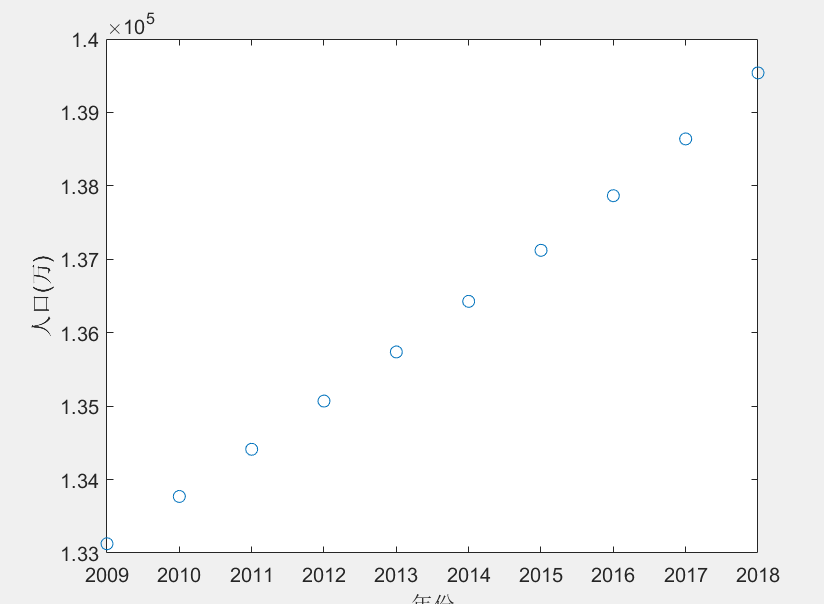
由图可知，人口数量曲线有明显的直线特征，故其函数表达式大致为y=kx+b。

运用最小二乘法

模型的求解

MATLAB 求解最小二乘

利用MATLAB软件我们求得\(k=702.4485,b=-1.2782×106\)，拟合的结果如下图所示：

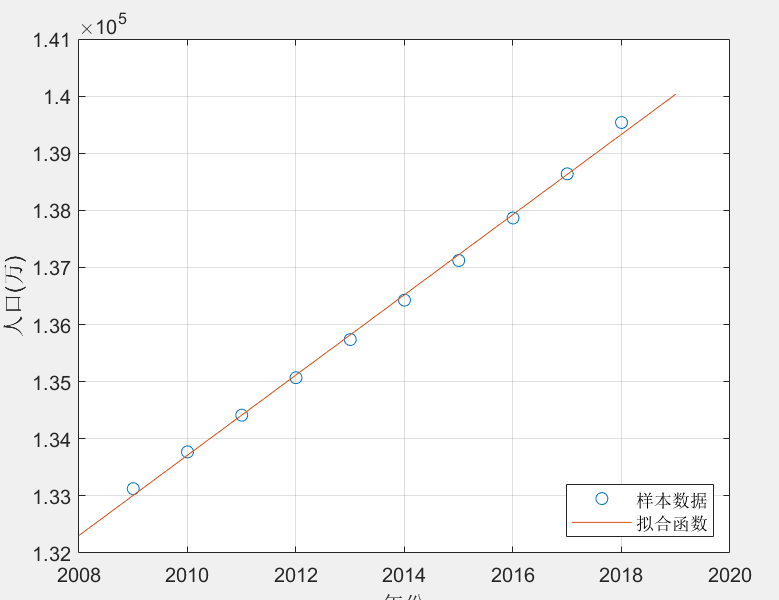
利用cftool工具箱

​ cftool是一款强大的由线拟合工具，且使用起来方便快捷，为了保正拟合结果的准确性，我们利用cftool工具箱选取了一些常见的拟合函数，并进行对比分析，结果如下表所示：

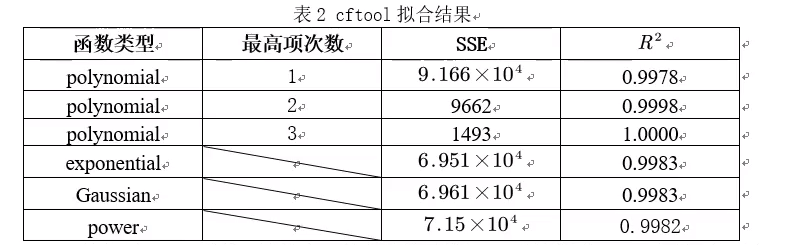
​ SSE越接近于0，说明误差越小即拟合的效果越好；对于线性模型，R2越接近于1，说明误差平方接近于0，拟的效果越好。但同时我们要考虑到函数的形式越简单越好，综合以上拟合结果，我们最终认为一次polynomial函数的拟合最为合适。

代码

%% 导入数据
[~, ~, raw] = xlsread('G:\数学建模学习材料\参考资料\清风数学建模\第1-14讲和番外篇的课件和代码(1月16日修订版本)\第1-14讲和番外篇课件和代码\第4讲.拟合\代码和例题数据\data2.xlsx','Sheet1','A2:B11');

%% 创建输出变量
data = reshape([raw{:}],size(raw));

%% 创建表
data2 = table;

%% 将导入的数组分配给列变量名称
x = data(:,1);
y = data(:,2);
cftool

%% 画图与建模
plot(x,y,'o')
xlabel('年份')
ylabel('人口(万)')
n = size(x,1);
k = (n*sum(x.*y)-sum(x)*sum(y))/(n*sum(x.*x)-sum(x)*sum(x))
b = (sum(x.*x)*sum(y)-sum(x)*sum(x.*y))/(n*sum(x.*x)-sum(x)*sum(x))
hold on % 继续在之前的图形上来画图形
grid on % 显示网格线
f=@(x) k*x+b;
fplot(f,[min(x)-1,max(x)+1])
legend('样本数据','拟合函数','location','SouthEast')

y_hat = k*x+b; % y的拟合值
SSR = sum((y_hat-mean(y)).^2)  % 回归平方和
SSE = sum((y_hat-y).^2) % 误差平方和
SST = sum((y-mean(y)).^2) % 总体平方和
SST-SSE-SSR   % 5.6843e-14  =   5.6843*10^-14   matlab浮点数计算的一个误差
R_2 = SSR / SST


[fitresult, gof] = createFit(x, y)

%% 清除临时变量
clearvars data raw;