聚类模型

学习视频：【强烈推荐】清风：数学建模算法、编程和写作培训的视频课程以及Matlab

老师讲得很详细，很受用！！！

定义

聚类就是将样本划分为由类似的对象组成的多个类的过程。聚类后，我们可以更加准确的在每个类中单独使用统计模型进行估计、分析或预测；也可以探究不同类之间的相关性和主要差异。

聚类和分类的区别:分类是已知类别的，聚类未知。

具体算法

K-means聚类算法

算法流程

  1. 指定需要划分的簇[cù]的个数K值（类的个数）;

  2. 随机地选择K个数据对象作为初始的聚类中心
    （不一定要是我们的样本点）;

  3. 计算其余的各个数据对象到这K个初始聚类中心的距离，把数据对象划归到距离它最近的那个中心所处在的簇类中;

  4. 调整新类并且重新计算出新类的中心;

  5. 五循环步骤3和4，看中心是否收敛（中心不变），如果收敛或达到迭代次数则停止循环;

  6. 结束。

    K‐均值聚类可视化的网站： https://www.naftaliharris.com/blog/v （强烈推荐试一下）

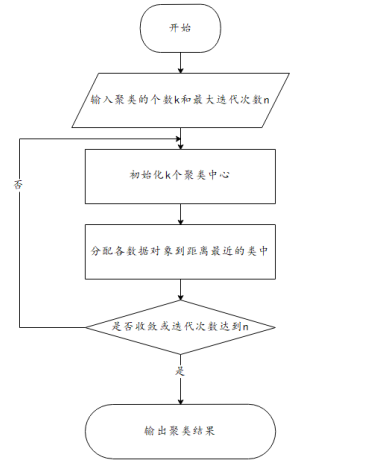
流程图

论文可以画，清晰明了！

优缺点

优点：
（1）算法简单、快速。
（2）对处理大数据集，该算法是相对高效率的。
缺点：
（1）要求用户必须事先给出要生成的簇的数目K。
（2）严重依赖与初始簇中心的选择，对初值敏感。
**（3）对于孤立点数据敏感。 **

**K‐means++算法可解决2、 3两个缺点。 **

K-means++算法

与K‐means++算法的区别

k-means++算法选择初始聚类中心的基本原则是： 初始的聚类中心之间的相互距离要尽可能的远。

算法描述如下：（只对K-means算法“初始化K个聚类中心” 这一步进行了优化）

  • 步骤一： 随机选取一个样本作为第一个聚类中心；
  • 步骤二： 计算每个样本与当前已有聚类中心的最短距离（即与最近一个聚类中心的距离），这个值越大，表示被选取作为聚类中心的概率较大；最后，用轮盘法（依据概率大小来进行抽选）选出下一个聚类中心；
  • 步骤三： 重复步骤二，直到选出K个聚类中心。选出初始点后，就继续使用标准的K-means算法了。

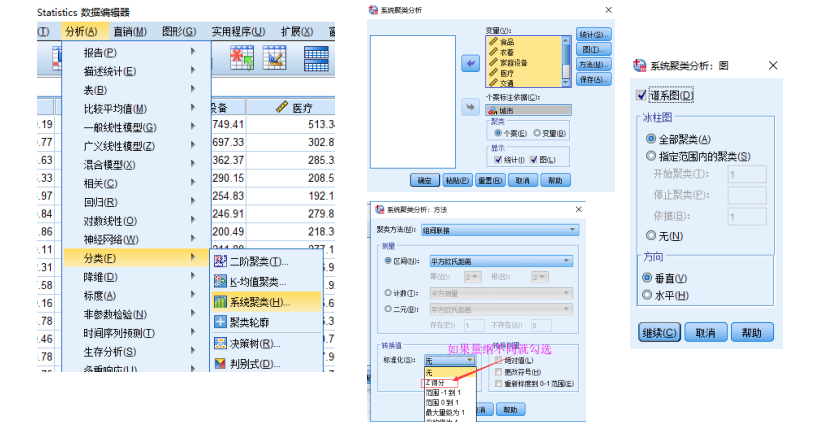
Spss软件操作

K-means算法的一些讨论

  1. 聚类的个数K值怎么定？
    答：分几类主要取决于个人的经验与感觉，通常的做法是多尝试几个K值，看分成几类的结果更好解释(高消费与低消费，或者高消费、中消费与低消费），更符合分析目的等。

  2. 数据的量纲不一致怎么办？
    答：如果数据的量纲不一样，那么算距离时就没有意义。例如：如果X1单位是米， X2单位是吨，用距离公式计算就会出现“米的平方”加上“吨的平方”再开平方，最后算出的东西没有数学意义，这就有问题了。

    具体做法：先减去均值再除以标准差

    \[z_{i}=\frac{x_{i}-\overline x}{\delta _{x}} \]

系统（层次）聚类 (可以查看k值)

​ 系统聚类的合并算法通过计算两类数据点间的距离，对最为接近的两类数据点进行组合，并反复迭代这一过程，直到将所有数据点合成一类，并生成聚类谱系图。

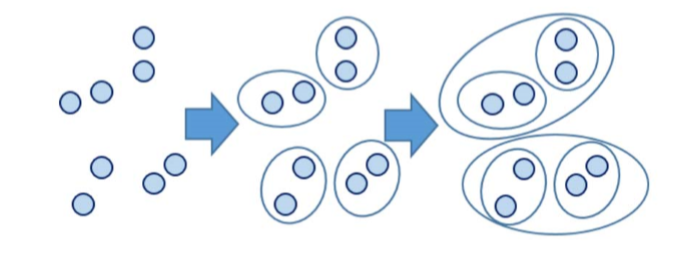
算法流程

系统（层次）聚类的算法流程：

  • 一、将每个对象看作一类，计算两两之间的最小距离；
  • 二、将距离最小的两个类合并成一个新类；
  • 三、重新计算新类与所有类之间的距离；
  • 四、重复二三两步，直到所有类最后合并成一类；
  • 五、结束。

详细讲解参考：于晶贤‐辽宁石油化工大学‐聚类分析之系统聚类法.pdf

常用距离（样品i与样品j）

  • 绝对值距离：网状结构的距离
  • 欧氏距离：一般就用欧式距离
  • Minkowski距离：
  • Chebyshev距离：
  • 马氏距离：多元正太分布

常用“距离” （指标i与指标j）

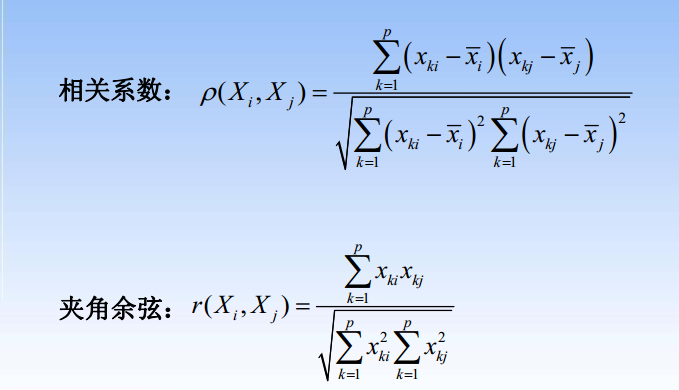
类与类之间的常用距离

1.由一个样品组成的类是最基本的类；如果每一类都由
个样品组成，那么样品间的距离就是类间距离。
2.如果某一类包含不止一个样品，那么就要确定类间距
离，类间距离是基于样品间距离定义的，大致有如下几种

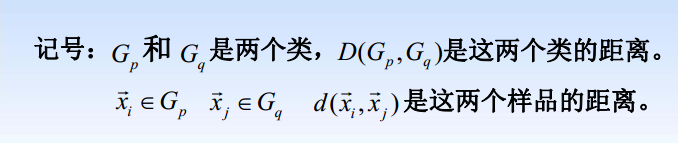
算法流程图

聚类分析需要注意的问题

1.对于一个实际问题要根据分类的目的来选取指标，指标
选取的不同分类结果一般也不同。
2.样品间距离定义方式的不同，聚类结果一般也不同。
3.聚类方法的不同，聚类结果一般也不同（尤其是样品特别多的时候）。最好能通过各种方法找出其中的共性。
4.要注意指标的量纲，量纲差别太大会导致聚类结果不合
理。
5.聚类分析的结果可能不令人满意，因为我们所做的是一个数学的处理，对于结果我们要找到一个合理的解释。

Spss软件操作

谱系图

画竖线可以看清分为多少类。

用图形估计聚类的数量

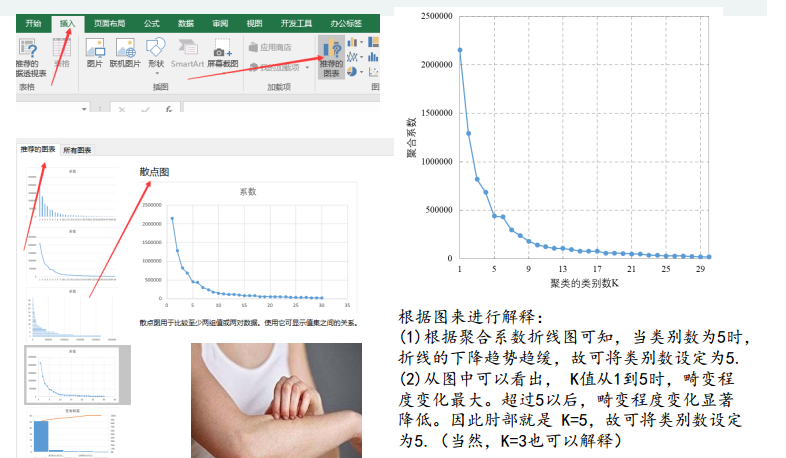
根据图来进行解释：
(1)根据聚合系数折线图可知，当类别数为5时，折线的下降趋势趋缓，故可将类别数设定为5.
(2)从图中可以看出， K值从1到5时，畸变程度变化最大。超过5以后，畸变程度变化显著降低。因此肘部就是 K=5，故可将类别数设定为5.（当然，K=3也可以解释）

确定K后保存聚类结果并画图

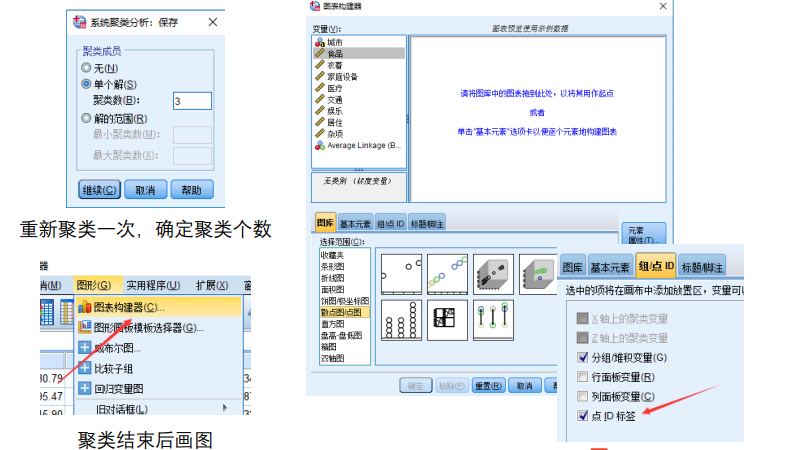
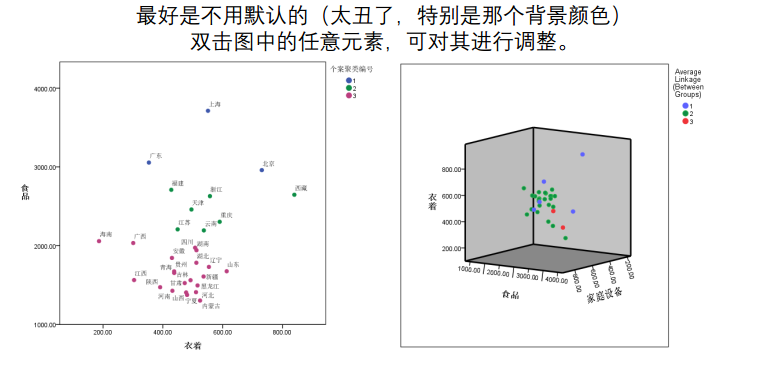
注意： 只要当指标个数为2或者3的时候才能画图，上面两个图纯粹是为了演示作图过程，实际上本例中指标个数有8个，是不可能做出这样的图的

DBSCAN算法

​ DBSCAN(Density-based spatial clustering of applications with noise)是Martin Ester, Hans-PeterKriegel等人于1996年提出的一种基于密度的聚类方法，聚类前不需要预先指定聚类的个数，生成的簇的个数不定（和数据有关）。该算法利用基于密度的聚类的概念，即要求聚类空间中的一定区域内所包含对象（点或其他空间对象）的数目不小于某一给定阈值。该方法能在具有噪声的空间数据库中发现任意形状的簇，可将密度足够大的相邻区域连接，能有效处理异常数据。

基本概念

DBSCAN算法将数据点分为三类：
• 核心点：在半径Eps内含有不少于MinPts数目的点
• 边界点：在半径Eps内点的数量小于MinPts，但是落在核心点的邻域内
• 噪音点：既不是核心点也不是边界点的点

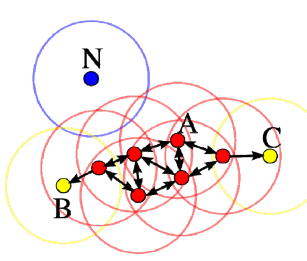
​ 在这幅图里，MinPts = 4，点 A 和其他红色点是核心点，因为它们的 ε-邻域（图中红色圆圈）里包含最少 4 个点（包括自己），由于它们之间相互相可达，它们形成了一个聚类。点 B 和点 C 不是核心点，但它们可由 A 经其他核心点可达，所以也和A属于同一个聚类。点 N 是局点，它既不是核心点，又不由其他点可达。

可视化

DBSCAN算法可视化

Matlab代码

Matlab官网推荐下载的代码：
https://ww2.mathworks.cn/matlabcentral/fileexchange/52905‐dbscan‐clustering‐algorithm

优缺点

优点：

  1. 基于密度定义，能处理任意形状和大小的簇；
  2. 可在聚类的同时发现异常点；
  3. 与K-means比较起来，不需要输入要划分的聚类个数。

缺点：

  1. 对输入参数ε和Minpts敏感，确定参数困难；

  2. 由于DBSCAN算法中，变量ε和Minpts是全局唯一的,当聚类的密度不均匀时，聚类距离相差很大时，聚类质量差；

  3. 当数据量大时，计算密度单元的计算复杂度大。

我的建议：

  1. 只有两个指标，且你做出散点图后发现数据表现得很“DBSCAN”，这时候你再用DNSCAN进行聚类。其他情况下，全部使用系统聚类吧。
  2. K‐means也可以用，不过用了的话你论文上可写的东西比较少。

作业

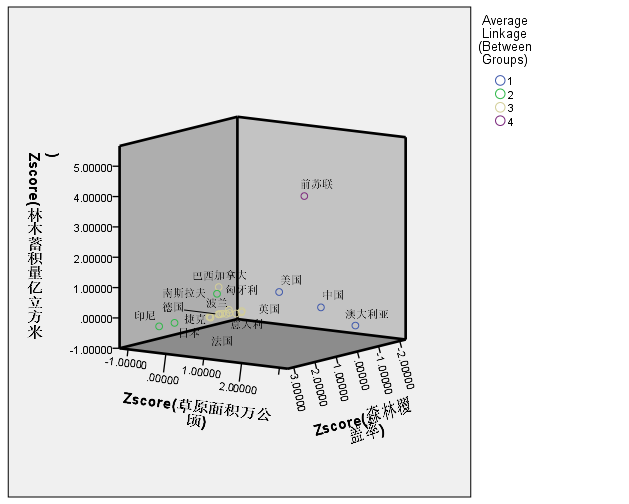
完成一篇论文作业，“各国森林、草原资源聚类.doc”，提示：指标共三个，量纲不同哦，论文中要交代清楚K的选择，当然你也可以画出你的聚类结果的三维图。

  1. 把作业表格复制到excel，用spss软件直接打开即可。

  2. 归一化变量

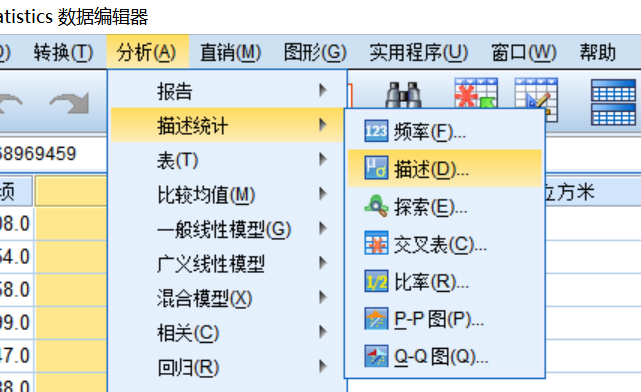
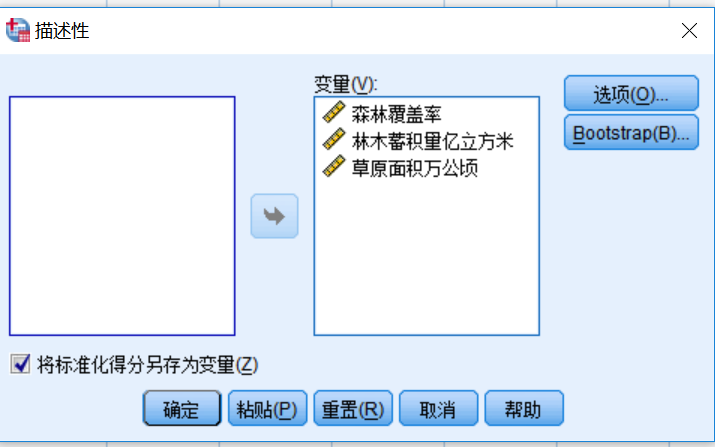
  3. 使用系统聚类和肘部法则确定聚类个数

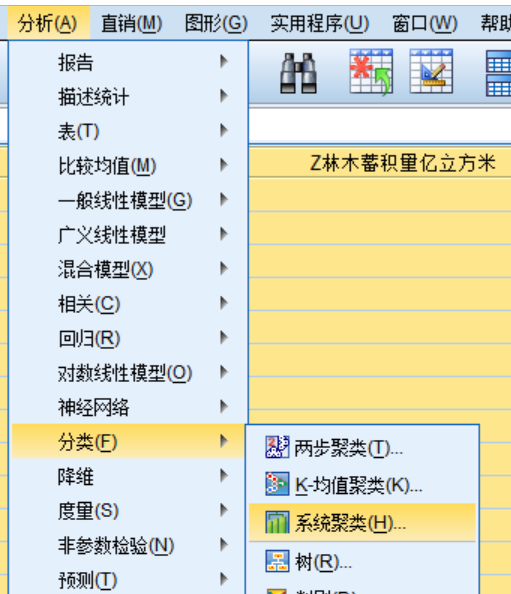
    在spss复制一下聚类系数

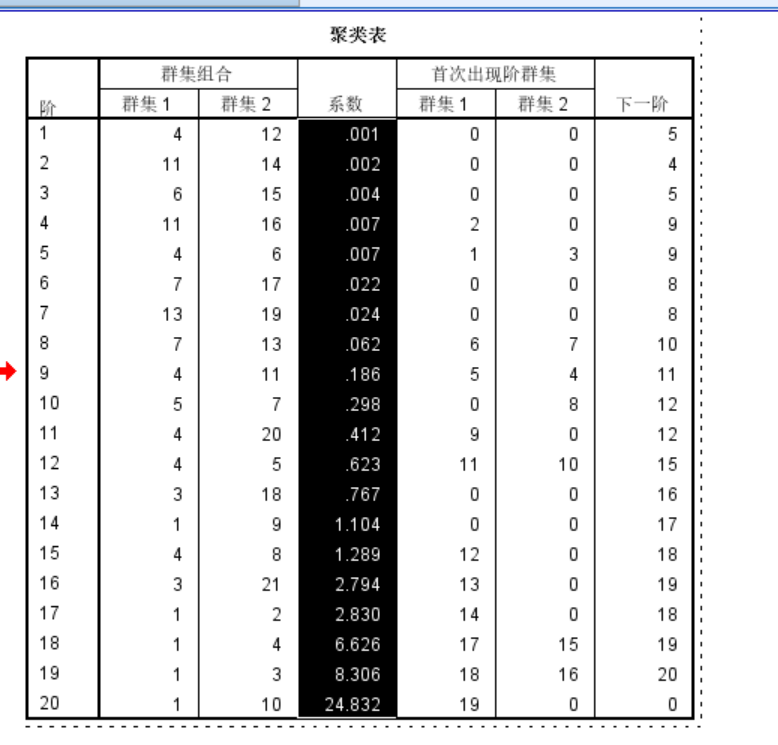
    复制到ECXCEL表里面去。

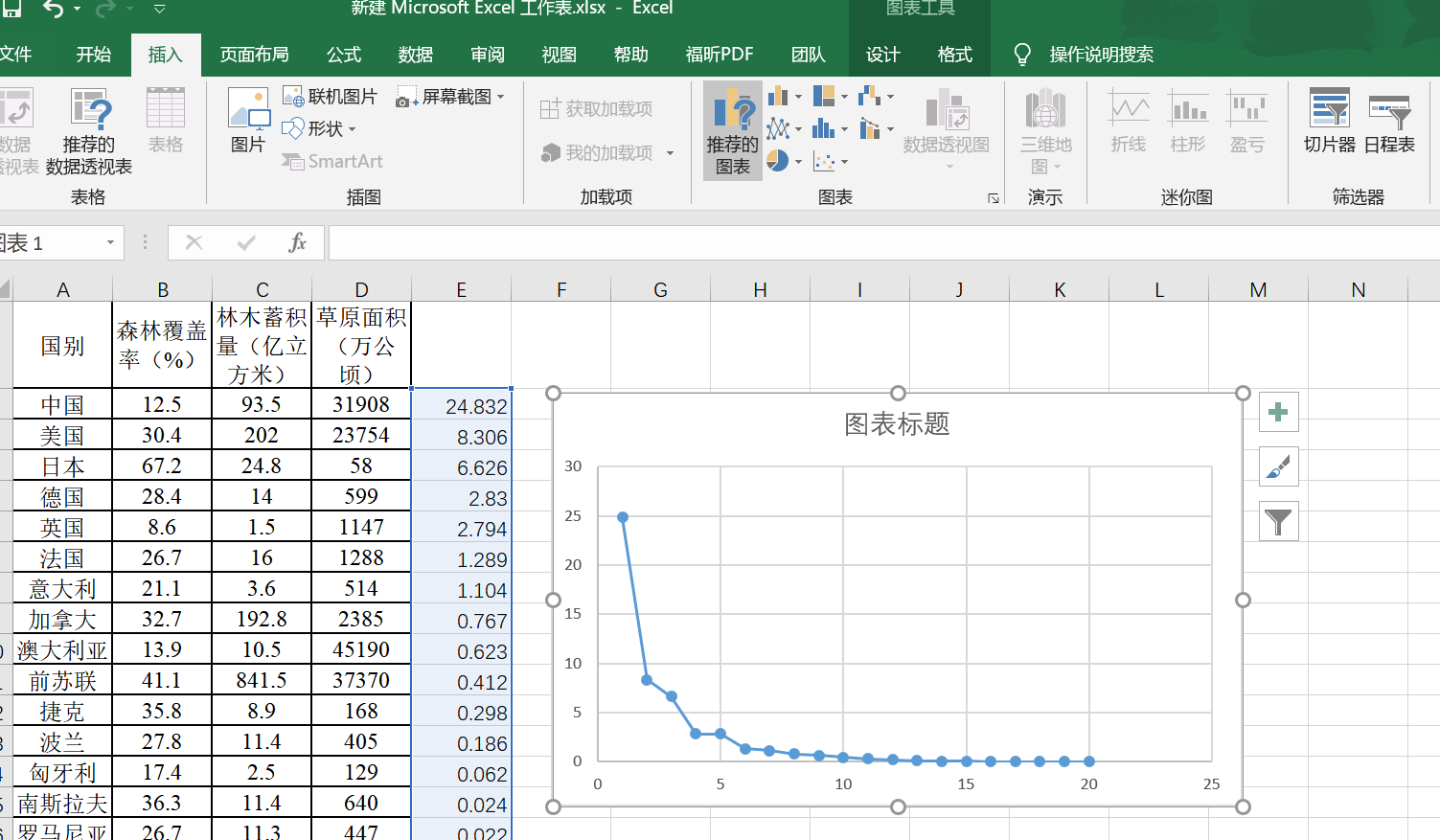
    通过对图像的观察分析，可以得出当聚类中心个数为4时，其聚合系数变化较大，所以选取聚类中心个数K=4。

  4. 真正的开始系统聚类(kmeans也行)

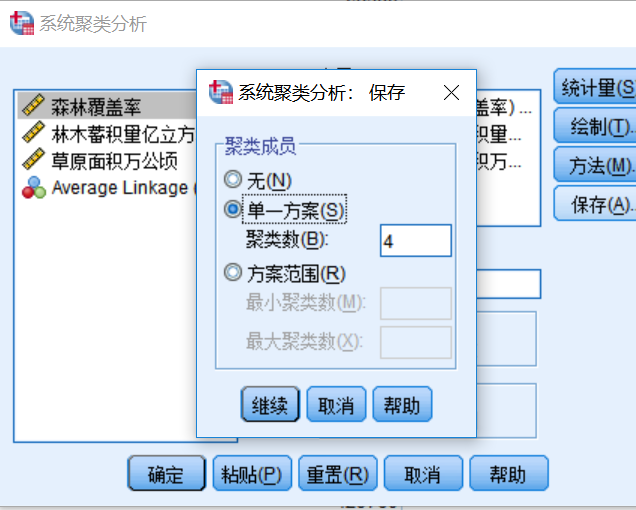
5.做散点图

posted @ 2020-02-10 22:20  pxlsdz  阅读(2161)  评论(0)  编辑  收藏  举报